1.simpletransformer包apex
它这个包默认的是如果使用GPU的话就是fp16精度,所以需要安装apex包,我还没有尝试过,既然它这么写肯定是考虑到显卡内存大小吧,所以我尝试一下安装apex:
https://github.com/NVIDIA/apex#quick-start,这个给出了步骤
$ git clone https://github.com/NVIDIA/apex $ cd apex $ pip install -v --no-cache-dir --global-option="--cpp_ext" --global-option="--cuda_ext" ./
ok没问题,可以安装成功。
但:cannot import name 'amp' from 'apex' (unknown location)
烦死了。https://github.com/NVIDIA/apex/issues/621,这里面遇到的问题和我一样,给出的办法是:https://github.com/NVIDIA/apex/issues/86#issuecomment-455620478
pip uninstall apex cd apex rm -rf build (if it exists) python setup.py install --cuda_ext --cpp_ext
但是我在最后一句,出现了这个问题:
FileNotFoundError: [Errno 2] No such file or directory: ':/usr/local/cuda/bin/nvcc': ':/usr/local/cuda/bin/nvcc'
对于这个问题我的猜测是,这个文件确实存在,我去文件夹下看了,确实存在,那可能就是权限的问题了,但是我用root用户去操作出现了一些conda的问题,我无法解决,而且我用
chmod +xxx nvcc文件,没有用,我猜测问题是因为nvcc文件所有者是root所以我无法访问?
又尝试chmod 777 nvcc,还是一样的问题,说明不是权限的问题。那可能的问题就是我的软链接,cuda默认会链接到cuda-10.0这个目录下。

搜到了相同的问题,解答https://github.com/NVIDIA/apex/issues/368#issuecomment-507533209,非常ok!
就:
export CUDA_HOME=/usr/local/cuda
而且我进入py环境:

就导入进来没问题??? 但是version就没有这个属性,而且我pip list 也根本就找不到apex这个包安装过啊。太迷惑了,隐藏安装???
安装过程好复杂,好慢卡住了吗。
可了!成功了!
以上均没有问题了。
2.torch手动梯度手动清零
https://www.zhihu.com/question/303070254?sort=created
这个高赞回答的也太好了,解决了我很多问题。这个和参数gradient_accumulation_steps一起来理解,简直完美!
使用梯度累加,可以让梯度计算过程实现更多的可能性:
for i,(images,target) in enumerate(train_loader): # 1. input output images = images.cuda(non_blocking=True) target = torch.from_numpy(np.array(target)).float().cuda(non_blocking=True) outputs = model(images) loss = criterion(outputs,target) # 2.1 loss regularization loss = loss/accumulation_steps # 2.2 back propagation loss.backward() # 3. update parameters of net if((i+1)%accumulation_steps)==0: # optimizer the net optimizer.step() # update parameters of net optimizer.zero_grad() # reset gradient

上面的讲解简直太牛了!怎么都懂这么多呢。反正使用梯度累加可以变相增加bs,缓解贫穷。
主要是因为torch会对梯度进行累加,所以需要清零!
下面的一个在内存占用大小方面来回答的也非常好!更理解了!
在前向的时候会计算梯度,这样就需要内存空间来保存,在loss.backward()之后这整个占用的空间就会被释放,原来计算的过程是这样的啊。
对于大bs,在计算梯度相关信息的时候需要的内存空间就大;所以可以选择小bs,和梯度累加来变相实现大bs。
5-3日————————
1.合并dict
https://blog.csdn.net/Jerry_1126/article/details/73017270
字典是Python语言中唯一的映射类型。
映射类型对象里哈希值(键,key)和指向的对象(值,value)是一对多的的关系,通常被认为是可变的哈希表。
使用items()更新,在python2中实现。

update,这个应该比较常用的:

2.什么是线性分类器/非线性分类器?
看到一篇论文中说,逻辑回归和SVM都是线性分类器???我迷惑。
https://www.cnblogs.com/BlueBlueSea/p/10291443.html,原来我那么久之前就已经学习过了啊!!!完全记不起来了。
上面这个链接里总结的回答已经很全面了,就已经过转换之后,逻辑回归的决策边界是线性的边界,
https://www.zhihu.com/question/30633734,这个回答下面。

关键点是:如果模型是参数的线性函数,并且存在线性分类面,那么就是线性分类器,否则不是。
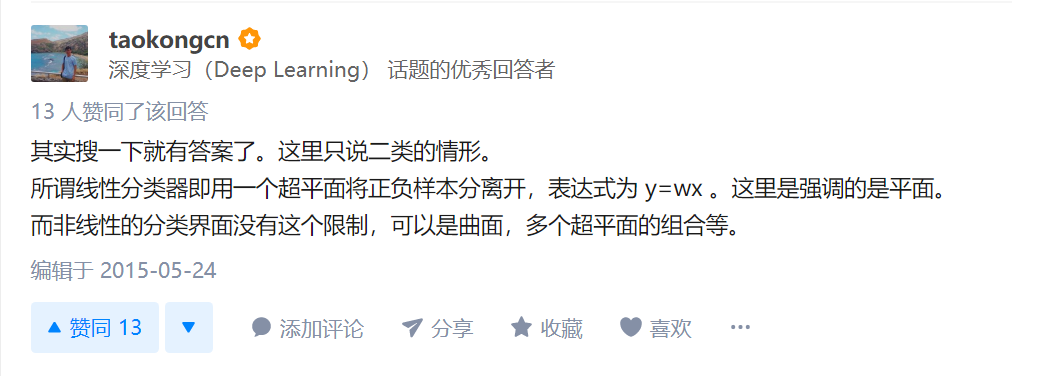
总结一下:对于二分类,线性分类只用一个超平面将其分开,但可能是引入到了更高维的空间;而非线性分类器是曲面,多个超平面的组和。
5-4日周一————
1.sklearn 交叉验证cross_val_score
https://blog.csdn.net/qq_36523839/article/details/80707678,这个给的例子还挺清楚的
from sklearn import datasets #自带数据集 from sklearn.model_selection import train_test_split,cross_val_score #划分数据 交叉验证 from sklearn.neighbors import KNeighborsClassifier #一个简单的模型,只有K一个参数,类似K-means import matplotlib.pyplot as plt iris = datasets.load_iris() #加载sklearn自带的数据集 X = iris.data #这是数据 y = iris.target #这是每个数据所对应的标签 train_X,test_X,train_y,test_y = train_test_split(X,y,test_size=1/3,random_state=3) #这里划分数据以1/3的来划分 训练集训练结果 测试集测试结果 k_range = range(1,31) cv_scores = [] #用来放每个模型的结果值 for n in k_range:#这个for循环是用来测试聚类成几类效果比较好的 knn = KNeighborsClassifier(n) #knn模型,这里一个超参数可以做预测,当多个超参数时需要使用另一种方法GridSearchCV scores = cross_val_score(knn,train_X,train_y,cv=10,scoring='accuracy') #cv:选择每次测试折数 accuracy:评价指标是准确度,可以省略使用默认值,具体使用参考下面。 cv_scores.append(scores.mean()) plt.plot(k_range,cv_scores) plt.xlabel('K') plt.ylabel('Accuracy') #通过图像选择最好的参数 plt.show() best_knn = KNeighborsClassifier(n_neighbors=3) # 选择最优的K=3传入模型 best_knn.fit(train_X,train_y) #训练模型 print(best_knn.score(test_X,test_y)) #看看评分
可以看到cross_val_score的参数,第一个参数是estimator,

estimator:estimator object implementing ‘fit’
The object to use to fit the data.
应该就是sklearn中实现的那些模型,比如linear_model等,带有fit方法的。
其他的参数还有数据集,交叉验证次数等。
2.sklearn的pipeline和FeatureUnion
https://blog.csdn.net/qq_35992440/article/details/89918305, 这个讲的不错,但我觉得我目前用不到
我觉得这个就是流水线性太强,机动性就比较弱,对于nlp类型的文本数据可能就适应度比较低?所以我先就不学习了。
3.sklearn使用总结
https://www.jianshu.com/p/516f009c0875,这个介绍的也太棒了,就对sk有一个宏观的理解了。