转自:https://blog.csdn.net/bitcarmanlee/article/details/51589143
在一篇博客中看到单变量线性回归可以使用最小二乘或者递归下降来求解,最小二乘就是最小化平方误差,解决最优化问题。
但是对其具体的过程还不是很理解,所以来总结学习一下。
1.最小二乘的代价函数
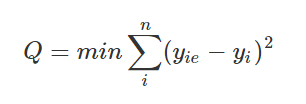
其中y_ie是估算值,y_i是真实值。其中求和是对n个样本的平方误差求和。
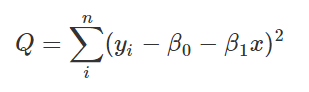
那么现在需要确定β0,β1,使得Q最小,那么分别偏导=0即可。也非常好求!
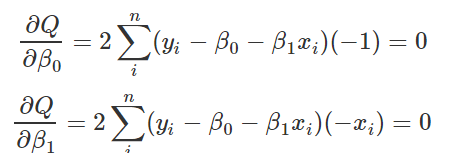
此时就根据上式写出,其实两个变量采用消元法,就可以,如果是克莱姆法则求解,分母是整个系数行列式,分子是等号右边替换本列系数变量形成的行列式。
最小二乘求出来的是精确值。
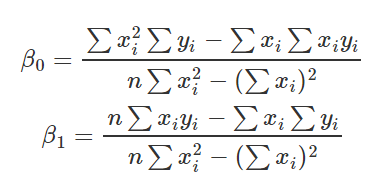
得出本式之后,只需要代入所有样本的x和y即可,因为是单变量,所以只有一个特征。
2.多个自变量-正规表达式
假如变量不止一个,也就是多变量的情况。

每个β都对应一个样本的特征。对于n个样本,线性方程组如下:
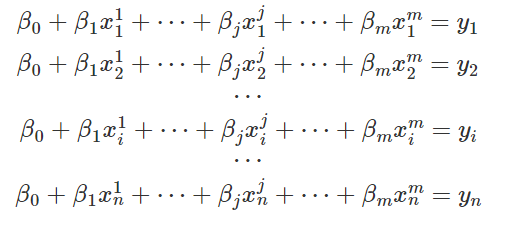
那么明显是可以写成矩阵的形式,如下:
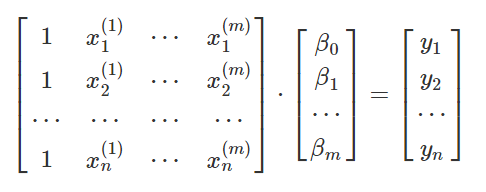
即Aβ=Y,其中A是样本值组成的系数矩阵,Y是模型预测值!。那么最终的代价函数可以写为:
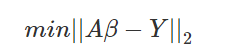
就是预测的值-真是值。此处应该是L2范数的平方吧,也就是向量长度的平方,没有根号。
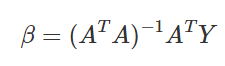
最终的最优解如图所示,但是我不知道是怎么推出来的。