CodeForces891BGluttony

B. Gluttony

time limit per test：2 seconds

memory limit per test：256 megabytes

input：standard input

output：standard output

You are given an array a with n distinct integers. Construct an array b by permuting a such that for every non-empty subset of indices S = {x1, x2, ..., xk} (1 ≤ xi ≤ n, 0 < k < n) the sums of elements on that positions in a and b are different, i. e.

Input

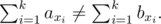
The first line contains one integer n (1 ≤ n ≤ 22) — the size of the array.

The second line contains n space-separated distinct integers a1, a2, ..., an (0 ≤ ai ≤ 10^9) — the elements of the array.

Output

If there is no such array b, print -1.

Otherwise in the only line print n space-separated integers b1, b2, ..., bn. Note that b must be a permutation of a.

If there are multiple answers, print any of them.

Examples

 

input

2

1 2

output

2 1

 

input

4

1000 100 10 1

output

100 1 1000 10 

 

Note

An array x is a permutation of y, if we can shuffle elements of y such that it will coincide with x.

Note that the empty subset and the subset containing all indices are not counted.

题解

考虑一个元素互异且升序的数列A，则易知满足题目条件的数列B = {A[n],A[1],...,A[n-1]}，即将A数列循环右移一个单位。为什么可以这样做？

由于A是升序的数列且元素互异，故对于任意的S = {x1, x2, ..., xk} (1 ≤ xi ≤ n, 0 < k < n)：

1. 若1 不在S内，则对于任意位置x_i (x_i ≠ 1) ，都有A[x_i] > B[x_i]，故∑^k_i=1A[x_i] > ∑^k_i=1B[x_i]，满足不相等条件；
2. 若1在S内，由于A[1]是A中最小的数，而B[1]是A中最大的数，且对于其他的位置x_i ≠ 1仍有A[x_i] > B[x_i]。又因为∑ⁿ_j=1A[j] = ∑ⁿ_j=1B[j]，除了位置1是A[1] < B[1]以外，其余位置j都是A[j] > B[j]，这就是说A[1]-B[1]的值需要其后n-1个位置的A[j]-B[j]的值来共同抵消，且1位置的A[1]-B[1]为负，其余n-1个位置的A[j]-B[j]均为正。也就是说，一旦S包含1，则要想∑^k_i=1A[x_i] = ∑^k_i=1B[x_i]必须有|S| = n，然而|s| < n，故有∑^k_i=1A[x_i] < ∑^k_i=1B[x_i]，仍然满足题意。
   

可见，如此获得的数列B即是A满足题意得一个排列，但题目中得数列a并不一定升序排列，所以我们可以记录原数列a中每一个数的下标后，对其进行升序排列，此时下标跟随着值的升序而打乱。然后将升序后的a数列的值（注意记录的数的下标不动）循环右移一个单位得到b，此时的b相对升序后的a满足题意。再将b和升序后的a数列按照记录的下标重新升序排列，a数列还原，此时得到新的b数列即为满足题意的数列。（因为排序过程并没有改变同一位置数列a和b数列相对应的值（即若a_i与b_j相对应于同一下标位置，排序后二者仍然是对应的），故原来的b数列是升序a数列的满足题意的数列，则排列后新的b数列则是升序a数列排列后（即原a数列）满足题意得数列）。也就是说对于满足题意得任意a数列，都有满足题意得b数列存在，故输出-1是不存在的。

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <string.h>
#include <algorithm>
#define re register
#define il inline
#define ll long long
#define ld long double
const ll MAXN = 1e6+5;
const ll INF = 1e8;

//快读
il ll read()
{
    char ch = getchar();
    ll res = 0, f = 1;
    while(ch < '0' || ch > '9')
    {
        if(ch == '-')   f = -1;
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9')
    {
        res = (res<<1) + (res<<3) + (ch-'0');
        ch = getchar();
    }
    return res*f;
}

//数列节点
struct A
{
    ll v, p;        //v为值，p为下标位置
};

//按值排序
bool cmpv(const A a1, const A a2)
{
    return a1.v < a2.v;
}

//按下标排序
bool cmpp(const A a1, const A a2)
{
    return a1.p < a2.p;
}

A a[MAXN], b[MAXN];

int main()
{
    ll n = read();
    for(re ll i = 1; i <= n; ++i)
    {
        a[i].v = read();
        a[i].p = i;
    }
    std::sort(a+1,a+n+1,cmpv);
    //将值整体循环右移一位
    b[1].v = a[n].v, b[1].p = a[1].p;
    for(re ll i = 2; i <= n; ++i)
    {
        b[i].v = a[i-1].v;
        b[i].p = a[i].p;
    }
    std::sort(b+1,b+n+1,cmpp);
    printf("%lld", b[1].v);
    for(re ll i = 2; i <= n; ++i)
    {
        printf(" %lld", b[i].v);
    }
    printf("\n");
    return 0;
}