【学习笔记】[图论]树的重心

非严格定义：树上任意一点都可以为根。对于某一点，若以它为根，则它的所有子树大小尽可能接近。

性质：

1. 树中所有点到某个点的距离和中，到重心的距离和是最小的，如果有两个/多个重心，到他们的距离和一样。

2. 把两棵树通过某一点相连得到一颗新的树，新的树的重心必然在连接原来两棵树重心的路径上。

3. 一棵树添加或者删除一个节点，树的重心最多只移动一条边的位置。

4. 对于任意一棵树，叶子节点不可能是这棵树的重心。特别地，只有两个结点的树例外。

求解方法：

思考可以得出如下事实：对于以任意一个结点作为根的所有最大子树中，以树的重心得出的最大子树最小。

所以，考虑用 DFS 遍历所有结点，每次求出以当前节点为根的最大子树的大小，记为 (f_u)。设最终答案为 (rt)，在遍历完某结点的所有儿子节点后，将求得的 (f_u) 与 (f_{rt}) 作比较，若小于，则令 (rt=u)。

另外，还需要解决一个问题。如图：

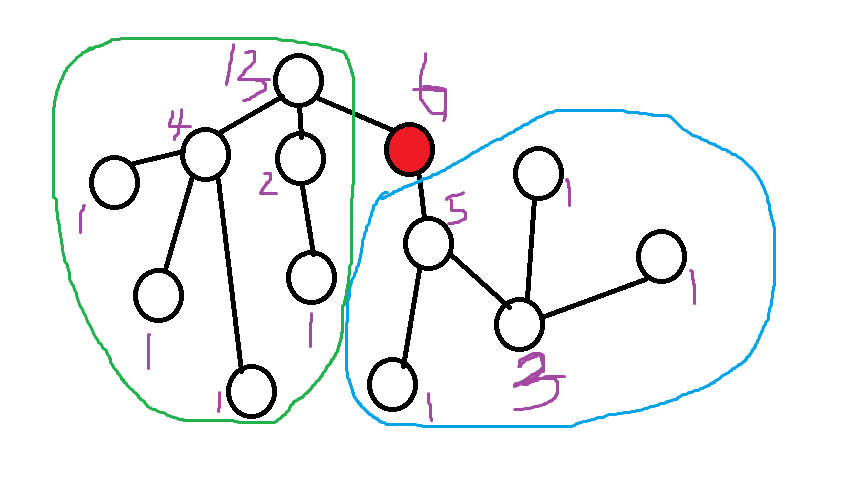
记 (size_u) 为结点 (u) 的树的大小。如上图紫色数字所示。

不难发现，对于蓝色部分，只需要递归去扫一遍，把每棵子树的大小加起来就好了。了。但是，对于绿色部分，不难发现它原来属于红色结点的“父辈”。换而言之，我们无法通过递归的方式得出绿色部分的大小。

解决办法很简单：利用类似前缀和的思想，用整棵树的大小（记位 (sum) ）减去除了“父辈”子树之外的子树大小。例如，对于上图， (sum=13)，用它减去除了绿色部分之外的子树大小 6 ，答案为 7 。而正确答案也是 7。

参考代码：

#include <iostream>
#include <cstdio>
#include <vector>
#include <cmath>

const int N=1000010;
const int inf=0x7f7f7f7f;

using namespace std;

int f[N],_size[N],n,tot;
//f[i]表示以i为根最大子树的值。重心需要找到一个最小的
//_size[i]代表这棵子树的大小
int rt,sum;
//rt是答案，sum是总点数
vector<int>G[N];

void addedge(int u,int v){G[u].push_back(v);G[v].push_back(u);}

inline void getrt(int u,int fa)
{
    _size[u]=1;f[u]=0; //f[u]：以每个结点为根，所以它的父亲都是0
    for(int i=0;i<G[u].size();i++)
    {
        int v=G[u][i];if(v==fa)continue;
        getrt(v,u); //把当前的每一个孩子当成根试一遍
        _size[u]+=_size[v]; //信息合并
        f[u]=max(f[u],_size[v]); //记录最大子树的大小
    }
    f[u]=max(f[u],sum-_size[u]); //sum是总点数
    //这里是在计算u上面的子树大小和下面最大的子树哪个大
    if(f[u]<f[rt])rt=u; //如果答案更优，就更新答案
}

inline int read()
{
    int w=1,s=0;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
    while(ch>='0'&&ch<='9')s=s*10+ch-'0',ch=getchar();
    return s*w;
}

int main()
{
    n=read();
    for(int i=1;i<=n;i++)
    {
        int u,v;u=read(),v=read();
        addedge(u,v);
    }
    rt=0;sum=n;f[0]=inf;getrt(1,0);
    cout<<rt<<endl;
    return 0;
}