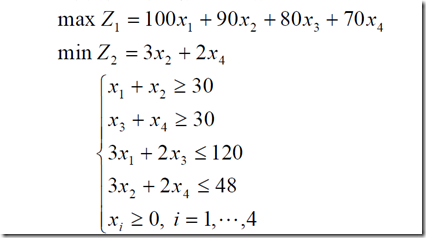求解多目标规划的思路
1、加权系数法
为每一个目标加一个权系数,把多目标模型转化成单一目标模型。但是困难时确定合理的权系数,以反映不同目标之间的重要程度。
2、优先等级法
将各目标按其重要程度分为不同的优先等级,转化为单目标模型。
3、有效解法
寻求能够照顾到各个目标,并使决策者感到满意的解。由决策者来确定选取哪一个解,即得到满意的解。但是有效解太多,无法挑选
一、目标规划的数学模型
1、正、负偏差变量
2、绝对约束和目标约束
(1)绝对约束:一定要达到的要求,线性规划的约束条件都是
(2)软约束(目标约束):就是在这个目标值允许有一定的正负偏差存在。
3、优先因子(优先等级)与权系数
一个规划问题如果有多个目标,可以按照重要性来规定一个优先因子P,越重要的越优先。
4、目标规划的目标函数
每一个目标值确定后,要求是尽可能小的缩小偏差。因此目标函数只能是![]() ,有三种形式
,有三种形式
(1)要求恰好达到目标值,即正负偏差都要小
(2)要求不超过目标值,正偏差小
(3)要求超过目标值,负偏差小
5、目标规划的一般数学模型
二、求解目标规划的序贯式模型
解题思路:
按照优先级的先后次序,将目标规划问题分解成一系列的单项目标规划问题。然后再依次求解。(由于使用LINGO求解,暂时忽略)
三、多目标规划的MATLAB解法
1、一般模型
2、MATLAB封装的函数
[x,fval]=fgoalattain('fun',x0,goal,weight,A,b,Aeq,beq,lb,ub,nonlcon)
(1)fun是用M文件定义的目标向量函数
(2)x0是初值,一般弄个随机列向量
(3)weight为权重,一般为goal的绝对值
(4)A,b定义不等式约束A*x<=b,Aeq,beq定义等式约束
(5)nonlcon是用M文件定义的非线性约束条件c(x)<=0,ceq(x)=0
(6)返回值,x是最优解,fval是最优值
3、例子
function F=Fun(x) F(1)=-100*x(1)-90*x(2)-80*x(3)-70*x(4); F(2)=3*x(2)+2*x(4);
a=[-1 -1 0 0 0 0 -1 -1 3 0 2 0 0 3 0 2]; b=[-30 -30 120 48]'; c1=[-100 -90 -80 -70]; c2=[0 3 0 2 ]; [x1,g1]=linprog(c1,a,b,[],[],zeros(4,1)) [x2,g2]=linprog(c2,a,b,[],[],zeros(4,1)) g3=[g1;g2]; [x,fval]=fgoalattain('Fun',rand(4,1),g3,abs(g3),a,b,[],[],zeros(4,1));