集训队日常训练20181124 DIV2

急急忙忙要出去比赛就拉了一场有点sb的题目

5202: 网络寻路 

时间限制(普通/Java):1000MS/3000MS     内存限制:65536KByte
总提交: 15            测试通过:12

描述

 

X 国的一个网络使用若干条线路连接若干个节点。节点间的通信是双向的。某重要数据包，为了安全起见，必须恰好被转发两次到达目的地。该包可能在任意一个节点产生，我们需要知道该网络中一共有多少种不同的转发路径。

源地址和目标地址可以相同，但中间节点必须不同。

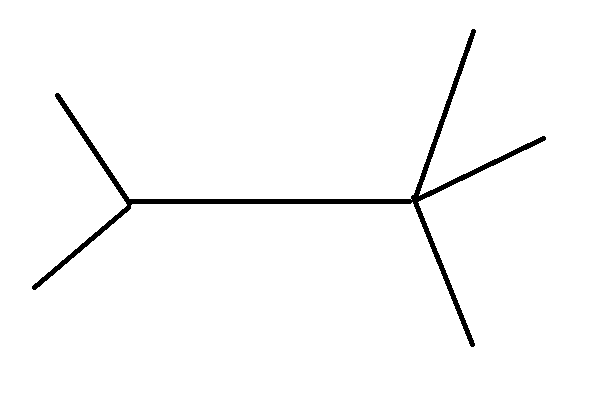
如下图所示的网络。

1 -> 2 -> 3 -> 1 是允许的

1 -> 2 -> 1 -> 2 或者 1 -> 2 -> 3 -> 2 都是非法的。

 

输入

 

输入数据的第一行为两个整数N M，分别表示节点个数和连接线路的条数(1<=N<=10000; 0<=M<=100000)。

接下去有M行，每行为两个整数 u 和 v，表示节点u 和 v 联通(1<=u,v<=N , u!=v)。

输入数据保证任意两点最多只有一条边连接，并且没有自己连自己的边，即不存在重边和自环。

 

输出

 

输出一个整数，表示满足要求的路径条数。

样例输入

 

3 3
1 2
2 3
1 3

样例输出

 6

提示

样例输入2

4 4
1 2
2 3
3 1
1 4

样例输出2

10

题目来源

蓝桥杯

可以dfs去枚举，也就是去枚举两边的点让他们不形成环

但是注意目的地可以和源地址相同，那么合法的就有以下两种情况

case1

case2

和当前节点的度有关，即这条边除了这条路带来的度的乘积

#include<bits/stdc++.h>
using namespace std;
const int N=100005;
int d[N],u[N],v[N],n,m;
int main()
{
    long long ans=0;
    scanf("%d%d",&n,&m);
    for(int i=0; i<m; i++)scanf("%d%d",&u[i],&v[i]),d[u[i]]++,d[v[i]]++;
    for(int i=0; i<m; i++)if(d[u[i]]>1&&d[v[i]]>1)ans+=(d[u[i]]-1)*1LL*(d[v[i]]-1)*2;
    printf("%I64d
",ans);
    return 0;
}

3198: 区间和 

时间限制(普通/Java):1000MS/3000MS     内存限制:65536KByte
总提交: 775            测试通过:247

描述

给定n个数据，有两个操作，加减其中的一个数据，当然还可查询在某段数据的和。

输入

 

输入数据有多组，每组数据的
第一行输入n，1=<n<=500000,代表数据的个数。
第二行输入具体数据，数据为正整数，范围在1到10000.
第三行输入m，1<=m<=100000,表示操作的次数。包含了修改和查询操作。
下面m行就是具体的操作了。
C i x  表示为第i个元素加上x，x范围在1到10000.
Q i j  表示查询区段i到j的和。保证输入的i<=j.
以EOF结束。

输出

输出查询后的区段和。

样例输入

8
1 5 9 11 2 8 15 6
4
Q 1 3
C 2 10
Q 1 4
Q 2 5

样例输出

15
36
37

提示

提示：类型最好定义为__int64

树状数组or线段树裸题，没接触过这种数据结构的可以看一下

涉及到区间修改区间查询，往往使用数据结构去维护

#include <stdio.h>
typedef __int64 ll;
const int N =500005;
ll c[N];
int n;
void read(int &x)
{
    char c;
    int ans=0;
    for(c=getchar(); c<'0'||c>'9'; c=getchar());
    while(c>='0'&&c<='9')
        ans=(ans<<1)+(ans<<3)+(c-'0'),c=getchar();
    x=ans;
}
int lowbit(int x)
{
    return x&-x;
}
void add(int x,int d)
{
    while(x<=n)
    {
        c[x]+=d;
        x+=lowbit(x);
    }
}
ll sum(int x)
{
    ll ans=0;
    while(x>0)
    {
        ans+=c[x];
        x-=lowbit(x);
    }
    return ans;
}
int main()
{
    while(~scanf("%d",&n))
    {
        for(int i=1;i<=n;i++)
            c[i]=0;
        for(int i=1;i<=n;i++)
        {
            int x;
            read(x);
            add(i,x);
        }
        int m;
        read(m);
        while(m--)
        {
            char c=getchar();
            int a,b;
            read(a),read(b);
            if(c=='Q')printf("%I64d
",sum(b)-sum(a-1));
            else add(a,b);
        }
    }
    return 0;
}

2686: 滑雪 

Time Limit(Common/Java):1000MS/10000MS     Memory Limit:65536KByte
Total Submit: 766            Accepted:218

Description

Michael喜欢滑雪百这并不奇怪， 因为滑雪的确很刺激。可是为了获得速度，滑的区域必须向下倾斜，而且当你滑到坡底，你不得不再次走上坡或者等待升降机来载你。Michael想知道载一个区域中最长底滑坡。区域由一个二维数组给出。数组的每个数字代表点的高度。下面是一个例子 

 1  2  3  4 5

16 17 18 19 6

15 24 25 20 7

14 23 22 21 8

13 12 11 10 9

一个人可以从某个点滑向上下左右相邻四个点之一，当且仅当高度减小。在上面的例子中，一条可滑行的滑坡为24-17-16-1。当然25-24-23-...-3-2-1更长。事实上，这是最长的一条。

Input

 

每组数据的第一行表示区域的行数R和列数C(1 <= R,C <= 100)。下面是R行，每行有C个整数，代表高度h，0<=h<=10000。输入以EOF结束

Output

输出最长区域的长度。

Sample Input

5 5
1 2 3 4 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9

Sample Output

 25

要找一条最长的递减序列，但是从一点开始的递减序列的长度我是可以记录的，比他大再到这个点也会有最长路径，所以就是一个记忆化搜索的问题

#include<stdio.h>
const int N=105;
int a[N][N],dp[N][N],r,c,t;
int dfs(int x,int y)
{
    int m=1;
    if(dp[x][y])return dp[x][y];
    if(x>0&&a[x-1][y]<a[x][y])t=dfs(x-1,y)+1,m=t<m?m:t;
    if(x<r-1&&a[x+1][y]<a[x][y])t=dfs(x+1,y)+1,m=t<m?m:t;
    if(y<c-1&&a[x][y+1]<a[x][y])t=dfs(x,y+1)+1,m=t<m?m:t;
    if(y>0&&a[x][y-1]<a[x][y])t=dfs(x,y-1)+1,m=t<m?m:t;
    return dp[x][y]=m;
}
int main()
{
    while(~scanf("%d%d",&r,&c))
    {
        for(int i=0; i<r; i++)
            for(int j=0; j<c; j++)
                scanf("%d",&a[i][j]),dp[i][j]=0;
        int m=0;
        for(int i=0; i<r; i++)
            for(int j=0; j<c; j++)
                if(dfs(i,j)>m)m=dp[i][j];
        printf("%d
",m);
    }
    return 0;
}

3097: 单词后缀 

Time Limit(Common/Java):1000MS/3000MS     Memory Limit:65536KByte
Total Submit: 670            Accepted:210

Description

有些英语单词后缀都是一样的，现在我们需要从给定的一堆单词里面找出某个后缀的单词个数。

Input

输入有多组数据。
每组第一行输入n，m，0<=n，m<=100000，
第二行到n+1行：输入单词，每个单词仅有小写英文字母组成，长度不超过10。
第n+2行到n+m+1行，输入要找的单词后缀。

Output

在n个单词里面找出输入单词后缀的单词个数，然后输出。每个数据与数据之间换行。

Sample Input

6 3
someone
everyone
outside
inside
somebody
nobody
one
side
body

Sample Output

2
2
2

字典树裸题

你用map的话带来了一个log的复杂度，但是你只是统计，使用C++的unordered_map也是可以过的

#include<bits/stdc++.h>
using namespace std;
unordered_map<string,int>ma;
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    string s;
    int n,m;
    while(cin>>n>>m)
    {
        for(int i=0; i<n; i++)
        {
            cin>>s;
            for(int j=0; s[j]; j++)ma[s.substr(j)]++;
        }
        while(m--)
        {
            string c;
            cin>>c;
            cout<<ma[c]<<endl;
        }
        ma.clear();
    }
    return 0;
}

1060: 鹊桥相会 

Time Limit(Common/Java):1000MS/10000MS     Memory Limit:65536KByte
Total Submit: 1471            Accepted:384

Description

一年一度的七夕又要到了，可歌可泣的牛郎织女又可以在鹊桥相会了。不知道大家有没有雅兴陪redraiment坐在葡萄藤下倾听他们的对话。 
我们知道，牛郎要与织女相见，必须要有喜鹊搭桥。所以，牛郎必须在天河岸上等待，直到有喜鹊经过，于是牛郎可以搭乘这只喜鹊往河对岸走。当然，牛郎急着去见织女，所以在途中，如果有速度更快的喜鹊赶上了他，他就会换乘那只速度更快的喜鹊。 
我们可以假定喜鹊的速度是恒定不变的，并且喜鹊一直是沿直线飞行的(不转弯，更不回头)，牛郎坐上喜鹊所花的时间忽略不计。 
现给出天河的宽度、每只喜鹊的初始位置(我们设牛郎所在位置为0，天河方向为正方向)以及它们的速度(有可能是负数，代表喜鹊往反方向飞行)，这些数据都是整数。请你来帮忙计算一下牛郎到达对岸与织女相会最少需要多少时间，让他们早些有情人终成眷属。^_^ 
当然，如果没有喜鹊来搭载牛郎，我们可怜的牛郎就到不了对岸与织女相会了，那我们只好很遗憾的跟牛郎说：“Can't Solve”，我们祈祷不要发生这样的事情。

Input

第一行有两个数据w、n，分别代表天河的宽度(单位:km)和喜鹊的只数(1≤w≤1000, 1≤n≤10000)。 
接下来从第二行到第n+1行每行都有两个数据t、v，分别代表1只喜鹊的初始位置(单位:m)和它的飞行速度(单位:m/s)(-1000≤t≤1000, -100≤v≤100)。 
所有的数据范围都不会超过32位整数的表示范围(用int型数据不会溢出)。 
输入以0 0结束。

Output

如果牛郎能到达对岸输出他到达对岸所花的总时间(结果精确到秒即可，小数部分舍去)；否则输出“Can't Solve”。

Sample Input

1 1
0 1
0 0

Sample Output

1000

这就是简单的小模拟，需要单位转换，注意细节就行了

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int main()
{
    int w,n;
    while(scanf("%d%d",&w,&n),w||n)
    {
        int ma=INT_MAX;
        for(int i=0,t,v; i<n; i++)
        {
            cin>>t>>v;
            if(t>0||v<=0)continue;
            int time=(1000*w-t)/v;
            if(time<ma)ma=time;
        }
        if(ma==INT_MAX)cout<<"Can't Solve
";
        else cout<<ma<<endl;
    }
    return 0;
}

1205: 斐波那契数列 

Time Limit(Common/Java):1000MS/10000MS     Memory Limit:65536KByte
Total Submit: 2476            Accepted:365

Description

一个斐波那契序列，F(0) = 0, F(1) = 1, F(n) = F(n-1) + F(n-2) (n>=2)，根据n的值，计算斐波那契数F(n)，其中0≤n≤1000。

Input

输入数据的第一行为测试用例的个数t，接下来为t行，每行为一个整数n（0≤n≤1000）。

Output

输出每个测试用例的斐波那契数F(n)。

Sample Input

2
1
2

Sample Output

1
1

大数模拟，不过这种题目还是直接上Java比较舒服，不会Java这个可以学习一下，算是比较常用的技巧了

solution from htmrc1

import java.math.BigInteger;
import java.util.Scanner;
public class Main {
    public static void main(String[] args) {
        Scanner cin=new Scanner(System.in);
        BigInteger []fib=new BigInteger[1010];
        fib[0]=BigInteger.valueOf(0);
        fib[1]=BigInteger.valueOf(1);
        for(int i=2;i<1005;++i)
        {
            fib[i]=fib[i-1].add(fib[i-2]);
        }
        int t=cin.nextInt();
        while(t-->0)
        {
            int n=cin.nextInt();
            System.out.println(fib[n]);
        }
    }
}

1237: 排名 

Time Limit(Common/Java):1000MS/10000MS     Memory Limit:65536KByte
Total Submit: 464            Accepted:214

Description

今天的上机考试虽然有实时的Ranklist，但上面的排名只是根据完成的题数排序，没有考虑 
每题的分值，所以并不是最后的排名。给定录取分数线，请你写程序找出最后通过分数线的 
考生，并将他们的成绩按降序打印。

Input

测试输入包含若干场考试的信息。每场考试信息的第1行给出考生人数N ( 0 < N 
< 1000 )、考题数M ( 0 < M < = 10 )、分数线（正整数）G；第2行排序给出第1题至第M题的正整数分值；以下N行，每行给出一 
名考生的准考证号（长度不超过20的字符串）、该生解决的题目总数m、以及这m道题的题号 
（题目号由1到M）。 
当读入的考生人数为0时，输入结束，该场考试不予处理。

Output

对每场考试，首先在第1行输出不低于分数线的考生人数n，随后n行按分数从高 
到低输出上线考生的考号与分数，其间用1空格分隔。若有多名考生分数相同，则按他们考 
号的升序输出。

Sample Input

4 5 25
10 10 12 13 15
CS004 3 5 1 3
CS003 5 2 4 1 3 5
CS002 2 1 2
CS001 3 2 3 5
1 2 40
10 30
CS001 1 2
2 3 20
10 10 10
CS000000000000000001 0
CS000000000000000002 2 1 2
0

Sample Output

3
CS003 60
CS001 37
CS004 37
0
1
CS000000000000000002 20

Source

G是真的模拟题，模拟就完事，所以我没懂为啥有人这个题目都没做

#include<stdio.h>
#include<string.h>
#include <algorithm>
using namespace std;
struct st
{
    char name[22];
    int score;
} data[1010];
int cmp(st a,st b)
{
    if(a.score!=b.score)
        return a.score>b.score;
    else if (strcmp(a.name,b.name)<0)
        return 1;
    else
        return 0;
}
int main()
{
    int i,n,m,l,x,k,sum,ans;
    while(scanf("%d",&n)&&n)
    {
        scanf("%d%d",&m,&l);
        int c[20]= {0};
        for(i=1; i<=m; i++)
        {
            scanf("%d",&c[i]);
        }
        for(i=1,ans=0; i<=n; i++)
        {
            sum=0;
            scanf("%s%d",data[i].name,&k);
            while(k--)
            {
                scanf("%d",&x);
                sum+=c[x];
            }
            data[i].score=sum;
            if(data[i].score>=l)
                ans++;
        }
        sort(data+1,data+n+1,cmp);
        printf("%d
",ans);
        for(i=1; i<=ans; i++)
            printf("%s %d
",data[i].name,data[i].score);
    }
    return 0;
}

1336: 小数化分数 

Time Limit(Common/Java):1000MS/10000MS     Memory Limit:65536KByte
Total Submit: 388            Accepted:220

Description

Ray 在数学课上听老师说，任何小数都能表示成分数的形式，他开始了化了起来，很快他就完成了，但他又想到一个问题，如何把一个循环小数化成分数呢?
请你写一个程序不但可以将普通小数化成最简分数，也可以把循环小数化成最简分数。

Input

第一行是一个整数N，表示有多少组数据。
每组数据只有一个纯小数，也就是整数部分为0。小数的位数不超过9位，循环部分用()括起来。

Output

对每一个对应的小数化成最简分数后输出，占一行。

Sample Input

3
0.(4)
0.5
0.32(692307)

Sample Output

4/9
1/2
17/52

 

循环小数的话其实都是与9有关，我的代码太丑了，就不放出来了，是一个挺有意思的题目

4261: 判断日期 

Time Limit(Common/Java):1000MS/3000MS     Memory Limit:65536KByte
Total Submit: 547            Accepted:111

Description

 

输入两个日期，输出较早的日期。如果输入的日期不合法则输入error！。

Input

 

测试数据有多组。输入格式为:年月日，年，月，日非负。

Output

 

输出：年-月-日，没有前导零

Sample Input

20121221
20121121
20121221
20121312

Sample Output

2012-11-21
error!

这种水题比较适合新生赛，练练手就好，其实没啥意义

#include <stdio.h>
static int valid_date(int y, int m, int d)
{
    int month[12]= {31,28,31,30,31,30,31,31,30,31,30,31};
    if((y%4==0&&y%100!=0)||y%400==0)
        month[1]=29;
    return m>0&&m<=12&&d>0&&d<=month[m-1];
}
int main()
{
    int y1,m1,d1,y2,m2,d2;
    while(scanf("%4d\%2d\%2d%4d\%2d\%2d",&y1,&m1,&d1,&y2,&m2,&d2)!=EOF)
    {
        if (valid_date(y1,m1,d1)&&valid_date(y2,m2,d2))
        {
            if(y1*10000+m1*100+d1>=y2*10000+m2*100+d2)
                printf("%d-%d-%d
",y2,m2,d2);
            else
                printf("%d-%d-%d
",y1,m1,d1);
        }
        else
            printf("error!
");
    }
    return 0;
}

4773: 回文数 

Time Limit(Common/Java):1000MS/3000MS     Memory Limit:65536KByte
Total Submit: 48            Accepted:13

Description

 

若一个数（首位不为0）从左到右读与从右到左读都是一样，这个数就叫做回文数，例如12521就是一个回文数。

 

给定一个N进制正整数，把它的各位数字上数字倒过来排列组成一个新数，然后与原数相加，如果是回文数则停止，如果不是，则重复这个操作，直到和为回文数为止。例如：10进制87则有：

STEP1: 87+78=165
STEP2: 165+561=726
STEP3: 726+627=1353
STEP4: 1353+3531=4884

 

任务：写一个程序，给定一个N（2≤N≤16）进制数m（10~15用大写字母A~F表示），m的位数上限为20。求最少经过几步可以得到回文数。如果在30步以内（包括30步）不可能得到回文数，则输出“Impossible”，否则输出生成该回文数的最少步数。

Input

 

输入有两行，每行一个数，即N和N进制整数m。

Output

 

若最少在30步以内得到回文数,则输出步数；

如果在30步以内（包含30步）不可能得到回文数，则输出“Impossible”(无引号)

Sample Input

9
87

Sample Output

6

这个同样去模拟就好了

最后一题更是个大模拟，学操作系统的你可以尝试一下