AtCoder Regular Contest 082

C - Together

---

Time limit : 2sec / Memory limit : 256MB

Score : 300 points

Problem Statement

You are given an integer sequence of length N, a1,a2,…,aN.

For each 1≤i≤N, you have three choices: add 1 to ai, subtract 1 from ai or do nothing.

After these operations, you select an integer X and count the number of i such that ai=X.

Maximize this count by making optimal choices.

Constraints

• 1≤N≤105
• 0≤ai<105(1≤i≤N)
• ai is an integer.

---

Input

The input is given from Standard Input in the following format:

N
a1 a2 .. aN

Output

Print the maximum possible number of i such that ai=X.

---

Sample Input 1

Copy

7
3 1 4 1 5 9 2

Sample Output 1

Copy

4

For example, turn the sequence into 2,2,3,2,6,9,2 and select X=2 to obtain 4, the maximum possible count.

---

Sample Input 2

Copy

10
0 1 2 3 4 5 6 7 8 9

Sample Output 2

Copy

3

---

Sample Input 3

Copy

1
99999

Sample Output 3

Copy

1

 这个题比较简单。就是每个数可以进行的操作是加1减一或者不变，贪心取三个就好啊

#include <stdio.h>
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int a[N];
int main()
{
    int n;
    cin>>n;
    for(int i=0; i<n; i++)
    {
        int x;
        cin>>x;
        a[x]++;
    }
    int ma=a[0]+a[1];
    for(int i=2;i<N;i++)
    {
        int t=a[i-2]+a[i-1]+a[i];
        if(t>ma)ma=t;
    }
    cout<<ma<<endl;
    return 0;
}

D - Derangement

---

Time limit : 2sec / Memory limit : 256MB

Score : 400 points

Problem Statement

You are given a permutation p1,p2,…,pN consisting of 1,2,..,N. You can perform the following operation any number of times (possibly zero):

Operation: Swap two adjacent elements in the permutation.

You want to have pi≠i for all 1≤i≤N. Find the minimum required number of operations to achieve this.

Constraints

• 2≤N≤105
• p1,p2,..,pN is a permutation of 1,2,..,N.

---

Input

The input is given from Standard Input in the following format:

N
p1 p2 .. pN

Output

Print the minimum required number of operations

---

Sample Input 1

Copy

5
1 4 3 5 2

Sample Output 1

Copy

2

Swap 1 and 4, then swap 1 and 3. p is now 4,3,1,5,2 and satisfies the condition. This is the minimum possible number, so the answer is 2.

---

Sample Input 2

Copy

2
1 2

Sample Output 2

Copy

1

Swapping 1 and 2 satisfies the condition.

---

Sample Input 3

Copy

2
2 1

Sample Output 3

Copy

0

The condition is already satisfied initially.

---

Sample Input 4

Copy

9
1 2 4 9 5 8 7 3 6

Sample Output 4

Copy

3

---

继续简单题，但是只能交换前后两个，所以正着扫一遍，倒着扫一遍就好的

#include <stdio.h>
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int a[N];
int main()
{
    int n;
    cin>>n;
    int t=0;
    for(int i=1; i<=n; i++)
    {
        int x;
        cin>>a[i];
    }
 
     for(int i=1; i<n; i++)
    {
        if(i==a[i])
        {swap(a[i],a[i+1]);t++;}
    }
     for(int i=n; i>1; i--)
    {
        if(i==a[i])
        {swap(a[i],a[i-1]);t++;}
    }
    cout<<t<<endl;
    return 0;
}

E - ConvexScore

---

Time limit : 2sec / Memory limit : 256MB

Score : 700 points

Problem Statement

You are given N points (xi,yi) located on a two-dimensional plane. Consider a subset S of the N points that forms a convex polygon. Here, we say a set of points Sforms a convex polygon when there exists a convex polygon with a positive area that has the same set of vertices as S. All the interior angles of the polygon must be strictly less than 180°.

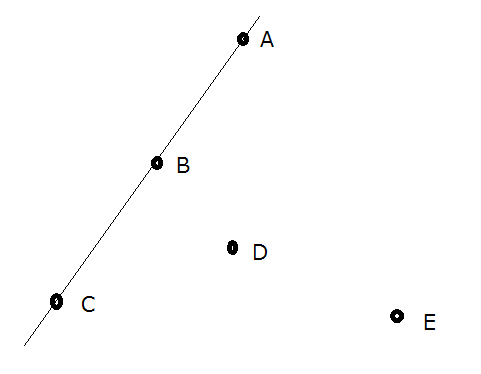
For example, in the figure above, {A,C,E} and {B,D,E} form convex polygons; {A,C,D,E}, {A,B,C,E}, {A,B,C}, {D,E} and {} do not.

For a given set S, let n be the number of the points among the N points that are inside the convex hull of S (including the boundary and vertices). Then, we will define the score of S as 2n−|S|.

Compute the scores of all possible sets S that form convex polygons, and find the sum of all those scores.

However, since the sum can be extremely large, print the sum modulo 998244353.

Constraints

• 1≤N≤200
• 0≤xi,yi<104(1≤i≤N)
• If i≠j, xi≠xj or yi≠yj.
• xi and yi are integers.

---

Input

The input is given from Standard Input in the following format:

N
x1 y1
x2 y2
:
xN yN

Output

Print the sum of all the scores modulo 998244353.

---

Sample Input 1

Copy

4
0 0
0 1
1 0
1 1

Sample Output 1

Copy

5

We have five possible sets as S, four sets that form triangles and one set that forms a square. Each of them has a score of 20=1, so the answer is 5.

---

Sample Input 2

Copy

5
0 0
0 1
0 2
0 3
1 1

Sample Output 2

Copy

11

We have three "triangles" with a score of 1 each, two "triangles" with a score of 2 each, and one "triangle" with a score of 4. Thus, the answer is 11.

---

Sample Input 3

Copy

1
3141 2718

Sample Output 3

Copy

0

There are no possible set as S, so the answer is 0.

给出一些点，每个凸多边形的贡献为2^n−|S|，求贡献和。

暴力枚举判断就好了

#include<cstdio>
int n,ans,x[210],y[210],f[210];
const int MD=998244353;
int main()
{
    scanf("%d",&n);
    f[0]=1;
    for(int i=1; i<=n; i++)
    {
        scanf("%d%d",&x[i],&y[i]);
        f[i]=1ll*f[i-1]*2%MD;
    }
    ans=f[n]-n-1;
    for(int i=1; i<=n; i++)
    {
        for(int j=i+1; j<=n; j++)
        {
            int d=0;
            for(int k=j+1; k<=n; k++)
            d+=(y[i]-y[j])*(x[i]-x[k])==(y[i]-y[k])*(x[i]-x[j]);
            ans=(ans+MD-f[d])%MD;
        }
    }
    printf("%d
",ans);
    return 0;
}