Polycarpus takes part in the "Field of Wonders" TV show. The participants of the show have to guess a hidden word as fast as possible. Initially all the letters of the word are hidden.
The game consists of several turns. At each turn the participant tells a letter and the TV show host responds if there is such letter in the word or not. If there is such letter then the host reveals all such letters. For example, if the hidden word is "abacaba" and the player tells the letter "a", the host will reveal letters at all positions, occupied by "a": 1, 3, 5 and 7 (positions are numbered from left to right starting from 1).
Polycarpus knows m words of exactly the same length as the hidden word. The hidden word is also known to him and appears as one of these m words.
At current moment a number of turns have already been made and some letters (possibly zero) of the hidden word are already revealed. Previously Polycarp has told exactly the letters which are currently revealed.
It is Polycarpus' turn. He wants to tell a letter in such a way, that the TV show host will assuredly reveal at least one more letter. Polycarpus cannot tell the letters, which are already revealed.
Your task is to help Polycarpus and find out the number of letters he can tell so that the show host will assuredly reveal at least one of the remaining letters.
The first line contains one integer n (1 ≤ n ≤ 50) — the length of the hidden word.
The following line describes already revealed letters. It contains the string of length n, which consists of lowercase Latin letters and symbols "*". If there is a letter at some position, then this letter was already revealed. If the position contains symbol "*", then the letter at this position has not been revealed yet. It is guaranteed, that at least one letter is still closed.
The third line contains an integer m (1 ≤ m ≤ 1000) — the number of words of length n, which Polycarpus knows. The following m lines contain the words themselves — n-letter strings of lowercase Latin letters. All words are distinct.
It is guaranteed that the hidden word appears as one of the given m words. Before the current move Polycarp has told exactly the letters which are currently revealed.
Output the single integer — the number of letters Polycarpus can tell so that the TV show host definitely reveals at least one more letter. It is possible that this number is zero.
4
a**d
2
abcd
acbd
2
5
lo*er
2
lover
loser
0
3
a*a
2
aaa
aba
1
In the first example Polycarpus can tell letters "b" and "c", which assuredly will be revealed.
The second example contains no letters which can be told as it is not clear, which of the letters "v" or "s" is located at the third position of the hidden word.
In the third example Polycarpus exactly knows that the hidden word is "aba", because in case it was "aaa", then the second letter "a" would have already been revealed in one of previous turns.
给一个字符串，该字符串中有*，*表示该位置是未知的，其余表示已知的。问你存在多少个字符，使得这种字符一定能转变至少一个*。直接枚举26个字符就可以了啊
#include <bits/stdc++.h> using namespace std; string s,a[1005]; int n,m,vis[1005],V[1005]; int main() { int ans=0; ios::sync_with_stdio(false); cin>>n>>s; for(int i=0; s[i]; i++) vis[s[i]-'a']=1; cin>>m; for(int i=0; i<m; i++) cin>>a[i]; for(int i=0; i<26; i++) { char c='a'+i; if(vis[c])continue; int ff=1; for(int j=0; j<m; j++) { memset(V,0,sizeof(V)); int f=1; for(int k=0; k<n; k++) { if(s[k]=='*'&&vis[a[j][k]-'a']) { f=0; break; } if(s[k]=='*')V[a[j][k]-'a']++; else if(s[k]!=a[j][k])f=0; } if(f&&V[i]==0)ff=0; } if(ff)ans++; } printf("%d ",ans); return 0; }
There are some ambiguities when one writes Berland names with the letters of the Latin alphabet.
For example, the Berland sound u can be written in the Latin alphabet as "u", and can be written as "oo". For this reason, two words "ulyana" and "oolyana" denote the same name.
The second ambiguity is about the Berland sound h: one can use both "h" and "kh" to write it. For example, the words "mihail" and "mikhail" denote the same name.
There are n users registered on the Polycarp's website. Each of them indicated a name represented by the Latin letters. How many distinct names are there among them, if two ambiguities described above are taken into account?
Formally, we assume that two words denote the same name, if using the replacements "u" 
"oo" and "h" "kh", you can make the words equal. One can make replacements in both directions, in any of the two words an arbitrary number of times. A letter that resulted from the previous replacement can participate in the next replacements.
For example, the following pairs of words denote the same name:
- "koouper" and "kuooper". Making the replacements described above, you can make both words to be equal: "koouper"
"kuuper" and "kuooper" "kuuper". - "khun" and "kkkhoon". With the replacements described above you can make both words to be equal: "khun" "khoon" and "kkkhoon" "kkhoon" "khoon".
For a given list of words, find the minimal number of groups where the words in each group denote the same name.
The first line contains integer number n (2 ≤ n ≤ 400) — number of the words in the list.
The following n lines contain words, one word per line. Each word consists of only lowercase Latin letters. The length of each word is between 1 and 20 letters inclusive.
Print the minimal number of groups where the words in each group denote the same name.
10
mihail
oolyana
kooooper
hoon
ulyana
koouper
mikhail
khun
kuooper
kkkhoon
4
9
hariton
hkariton
buoi
kkkhariton
boooi
bui
khariton
boui
boi
5
2
alex
alex
1
There are four groups of words in the first example. Words in each group denote same name:
- "mihail", "mikhail"
- "oolyana", "ulyana"
- "kooooper", "koouper"
- "hoon", "khun", "kkkhoon"
There are five groups of words in the second example. Words in each group denote same name:
- "hariton", "kkkhariton", "khariton"
- "hkariton"
- "buoi", "boooi", "boui"
- "bui"
- "boi"
In the third example the words are equal, so they denote the same name.
可以这样xjb变，u" 变"oo" and "h" 变"kh"，有h了就可以无限消k，你给他们变到一种上，问有几种
#include <bits/stdc++.h> using namespace std; int n,ans; char s[1005]; map<string,bool> vis; int main() { scanf("%d",&n); for(int i=1; i<=n; i++) { scanf("%s",s+1); int m=strlen(s+1); string c=""; for(int j=m; j>0; j--) if(s[j]=='u') c="oo"+c; else if(s[j]=='h') { int l=j-1; while(l&&s[l]=='k') l--; j=l+1; c='h'+c; } else c=s[j]+c; if(!vis[c]) ans++,vis[c]=1; } printf("%d ",ans); return 0; }
Kolya has a string s of length n consisting of lowercase and uppercase Latin letters and digits.
He wants to rearrange the symbols in s and cut it into the minimum number of parts so that each part is a palindrome and all parts have the same lengths. A palindrome is a string which reads the same backward as forward, such as madam or racecar.
Your task is to help Kolya and determine the minimum number of palindromes of equal lengths to cut s into, if it is allowed to rearrange letters in s before cuttings.
The first line contains an integer n (1 ≤ n ≤ 4·105) — the length of string s.
The second line contains a string s of length n consisting of lowercase and uppercase Latin letters and digits.
Print to the first line an integer k — minimum number of palindromes into which you can cut a given string.
Print to the second line k strings — the palindromes themselves. Separate them by a space. You are allowed to print palindromes in arbitrary order. All of them should have the same length.
6
aabaac
2
aba aca
8
0rTrT022
1
02TrrT20
2
aA
2
a A
给你一个长度为n的字符串，让你把他处理成回文子串，问你最少分成几个串
看成对的字母有多少个，贪心处理下吧，奇数的放中间，偶数扔两边
#include<bits/stdc++.h> using namespace std; const int N=4e5+5; char s[N]; int a[N],b[N]; int A,B,n,t[256]; int main() { scanf("%d",&n); scanf("%s",s+1); for(int i=1; i<=n; i++) t[s[i]]++; for(int i=0; i<256; i++) { for(int j=1; j<=t[i]/2; j++)a[++A]=i; if(t[i]&1)b[++B]=i; } if(!B) { printf("%d ",1); for(int i=1; i<=A; i++)putchar(a[i]); for(int i=A; i>=1; i--)putchar(a[i]); return 0; } for(int i=1; i<=n; i++) if(n%i==0) { if(n/i%2==0)continue; int r=(n/i-1)/2; if(A<r*i)continue; printf("%d ",i); for(int j=r*i+1; j<=A; j++) { b[++B]=a[j]; b[++B]=a[j]; } for(int j=1; j<=i; j++) { for(int k=(j-1)*r+1; k<=j*r; k++)putchar(a[k]); putchar(b[j]); for(int k=j*r; k>=(j-1)*r+1; k--)putchar(a[k]); putchar(' '); } return 0; } }
Polycarp takes part in a quadcopter competition. According to the rules a flying robot should:
- start the race from some point of a field,
- go around the flag,
- close cycle returning back to the starting point.
Polycarp knows the coordinates of the starting point (x1, y1) and the coordinates of the point where the flag is situated (x2, y2). Polycarp’s quadcopter can fly only parallel to the sides of the field each tick changing exactly one coordinate by 1. It means that in one tick the quadcopter can fly from the point (x, y) to any of four points: (x - 1, y), (x + 1, y), (x, y - 1) or (x, y + 1).
Thus the quadcopter path is a closed cycle starting and finishing in (x1, y1) and containing the point (x2, y2) strictly inside.
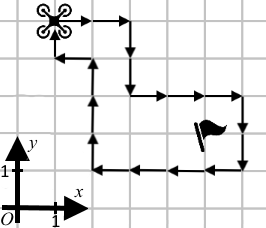The picture corresponds to the first example: the starting (and finishing) point is in (1, 5) and the flag is in (5, 2).What is the minimal length of the quadcopter path?
The first line contains two integer numbers x1 and y1 ( - 100 ≤ x1, y1 ≤ 100) — coordinates of the quadcopter starting (and finishing) point.
The second line contains two integer numbers x2 and y2 ( - 100 ≤ x2, y2 ≤ 100) — coordinates of the flag.
It is guaranteed that the quadcopter starting point and the flag do not coincide.
Print the length of minimal path of the quadcopter to surround the flag and return back.
1 5
5 2
18
0 1
0 0
8
#include<bits/stdc++.h> using namespace std; int main() { int x1,y1,x2,y2; scanf("%d%d%d%d",&x1,&y1,&x2,&y2); printf("%d ",4+max(abs(x1-x2),1)*2+max(abs(y1-y2),1)*2); }