靠这把上了蓝
You are given a string A. Find a string B, where B is a palindrome and A is a subsequence of B.
A subsequence of a string is a string that can be derived from it by deleting some (not necessarily consecutive) characters without changing the order of the remaining characters. For example, "cotst" is a subsequence of "contest".
A palindrome is a string that reads the same forward or backward.
The length of string B should be at most 104. It is guaranteed that there always exists such string.
You do not need to find the shortest answer, the only restriction is that the length of string B should not exceed 104.
First line contains a string A (1 ≤ |A| ≤ 103) consisting of lowercase Latin letters, where |A| is a length of A.
Output single line containing B consisting of only lowercase Latin letters. You do not need to find the shortest answer, the only restriction is that the length of string B should not exceed 104. If there are many possible B, print any of them.
aba
aba
ab
aabaa
In the first example, "aba" is a subsequence of "aba" which is a palindrome.
In the second example, "ab" is a subsequence of "aabaa" which is a palindrome.
输出一个字符串是输入串的子串，并且是回文串，不要求最短
#include<bits/stdc++.h> using namespace std; typedef long long ll; const int N=1e5+5; int main() { ios::sync_with_stdio(false); string s; cin>>s; cout<<s; reverse(s.begin(),s.end()); cout<<s; return 0; }
Let us define two functions f and g on positive integer numbers.
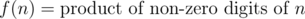
You need to process Q queries. In each query, you will be given three integers l, r and k. You need to print the number of integers xbetween l and r inclusive, such that g(x) = k.
The first line of the input contains an integer Q (1 ≤ Q ≤ 2 × 105) representing the number of queries.
Q lines follow, each of which contains 3 integers l, r and k (1 ≤ l ≤ r ≤ 106, 1 ≤ k ≤ 9).
For each query, print a single line containing the answer for that query.
4
22 73 9
45 64 6
47 55 7
2 62 4
1
4
0
8
4
82 94 6
56 67 4
28 59 9
39 74 4
3
1
1
5
In the first example:
- g(33) = 9 as g(33) = g(3 × 3) = g(9) = 9
- g(47) = g(48) = g(60) = g(61) = 6
- There are no such integers between 47 and 55.
- g(4) = g(14) = g(22) = g(27) = g(39) = g(40) = g(41) = g(58) = 4
他本来是递归函数，我们需要先预处理就可以了
#include<bits/stdc++.h> using namespace std; typedef long long ll; const int N=1e6+5; int a[N][10]; int main() { ios::sync_with_stdio(false); for(int i=1;i<=1e6;i++) { int t=i; while(t>=10) { int s=1; while(t) { if(t%10)s*=t%10; t/=10; } t=s; } for(int j=1;j<10;j++) a[i][j]=a[i-1][j]+(t==j); } int T; cin>>T; while(T--) { int l,r,k; cin>>l>>r>>k; cout<<a[r][k]-a[l-1][k]<<" "; } return 0; }
For a permutation P[1... N] of integers from 1 to N, function f is defined as follows:
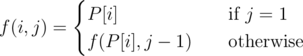
Let g(i) be the minimum positive integer j such that f(i, j) = i. We can show such j always exists.
For given N, A, B, find a permutation P of integers from 1 to N such that for 1 ≤ i ≤ N, g(i) equals either A or B.
The only line contains three integers N, A, B (1 ≤ N ≤ 106, 1 ≤ A, B ≤ N).
If no such permutation exists, output -1. Otherwise, output a permutation of integers from 1 to N.
9 2 5
6 5 8 3 4 1 9 2 7
3 2 1
1 2 3
In the first example, g(1) = g(6) = g(7) = g(9) = 2 and g(2) = g(3) = g(4) = g(5) = g(8) = 5
In the second example, g(1) = g(2) = g(3) = 1
递归版的轮换，一组等于a，一组等于b即可
#include<bits/stdc++.h> using namespace std; int main() { int n,a,b,f=1,fa,fb; cin>>n>>a>>b; if(b>a)swap(a,b); for(int i=0; i<=n&&f; i+=a) if((n-i)%b==0) fa=i/a,fb=(n-i)/b,f=0; if(f) cout<<-1; else { int i=1; for(; i<=fa*a; i+=a) { cout<<i+a-1<<" "; for(int j=i; j<i+a-1; j++) cout<<j<<" "; } for(; i<=n; i+=b) { cout<<i+b-1<<" "; for(int j=i; j<i+b-1; j++) cout<<j<<" "; } } return 0; }
You are given a node of the tree with index 1 and with weight 0. Let cnt be the number of nodes in the tree at any instant (initially, cnt is set to 1). Support Q queries of following two types:
Add a new node (index cnt + 1) with weight W and add edge between node R and this node.
Output the maximum length of sequence of nodes which- starts with R.
- Every node in the sequence is an ancestor of its predecessor.
- Sum of weight of nodes in sequence does not exceed X.
- For some nodes i, j that are consecutive in the sequence if i is an ancestor of j then w[i] ≥ w[j] and there should not exist a node k on simple path from i to j such that w[k] ≥ w[j]
The tree is rooted at node 1 at any instant.
Note that the queries are given in a modified way.
First line containing the number of queries Q (1 ≤ Q ≤ 400000).
Let last be the answer for previous query of type 2 (initially last equals 0).
Each of the next Q lines contains a query of following form:
- 1 p q (1 ≤ p, q ≤ 1018): This is query of first type where
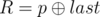and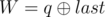 
. It is guaranteed that 1 ≤ R ≤ cnt and 0 ≤ W ≤ 109. - 2 p q (1 ≤ p, q ≤ 1018): This is query of second type where 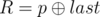and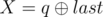
. It is guaranteed that 1 ≤ R ≤ cntand 0 ≤ X ≤ 1015.
denotes bitwise XOR of a and b.
It is guaranteed that at least one query of type 2 exists.
Output the answer to each query of second type in separate line.
6
1 1 1
2 2 0
2 2 1
1 3 0
2 2 0
2 2 2
0
1
1
2
6
1 1 0
2 2 0
2 0 3
1 0 2
2 1 3
2 1 6
2
2
3
2
7
1 1 2
1 2 3
2 3 3
1 0 0
1 5 1
2 5 0
2 4 0
1
1
2
7
1 1 3
1 2 3
2 3 4
1 2 0
1 5 3
2 5 5
2 7 22
1
2
3
In the first example,
last = 0
- Query 1: 1 1 1, Node 2 with weight 1 is added to node 1.
- Query 2: 2 2 0, No sequence of nodes starting at 2 has weight less than or equal to 0. last = 0
- Query 3: 2 2 1, Answer is 1 as sequence will be {2}. last = 1
- Query 4: 1 2 1, Node 3 with weight 1 is added to node 2.
- Query 5: 2 3 1, Answer is 1 as sequence will be {3}. Node 2 cannot be added as sum of weights cannot be greater than 1. last = 1
- Query 6: 2 3 3, Answer is 2 as sequence will be {3, 2}. last = 2
对于一棵树，你有2种操作