【杭电】[5660]jrMz and angles

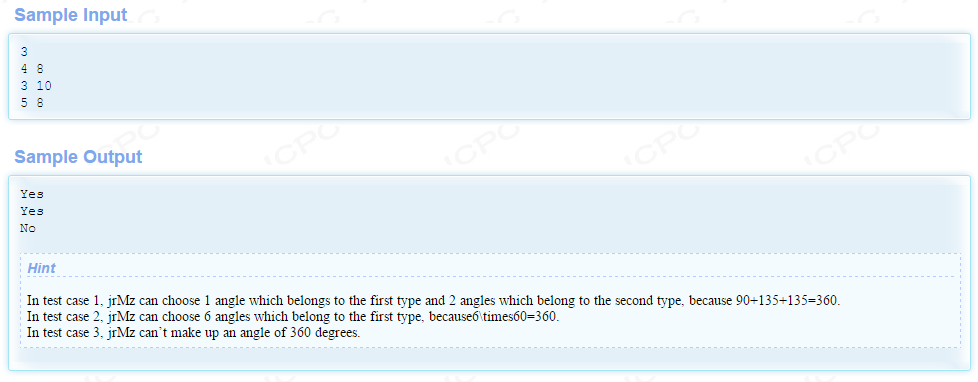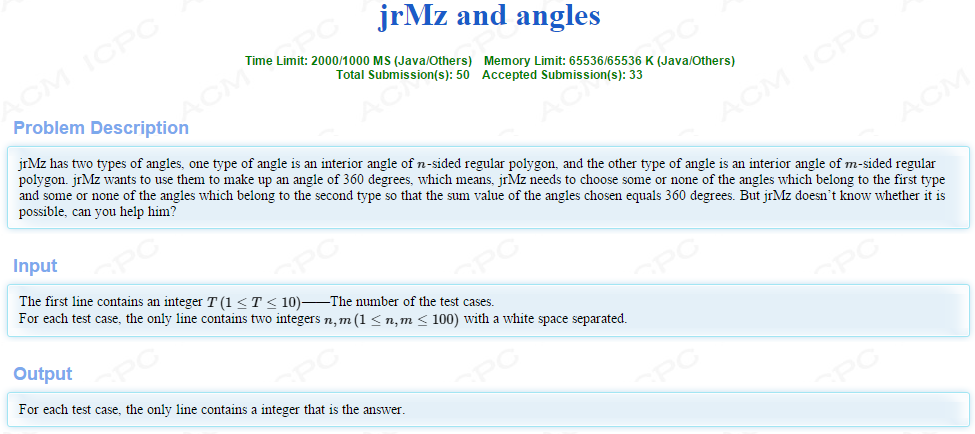
原先是想按照二元一次方程有无整数解来求

于是写出WA的……

#include<stdio.h>
int gcd(int a,int b) {
    if(b==0)
        return a;
    else
        return gcd(b,a%b);
}
int main() {
    int T;
    scanf("%d",&T);
    while(T--) {
        int n,m;
        scanf("%d %d",&n,&m);
        int ta=180*n-360;
        int tb=180*m-360;
        if((360*n*m)%gcd(ta,tb)==0)
            printf("Yes
");
        else
            printf("No
");
    }
    return 0;
}
//WA原因:解可能为负数 

因为没有考虑虽有整数解
但是整数解为负值的情况
所以WA

根据题解写的AC:

#include<stdio.h>
int main() {
    int T;
    scanf("%d",&T);
    while(T--) {
        int n,m;
        scanf("%d %d",&n,&m);
        if(n==3||n==4||n==6||m==3||m==4||m==6||(n==5&&m==10)||(n==10&&m==5))
            printf("Yes
");
        else
            printf("No
");
    }
    return 0;
}

也许在接触扩展欧几里得之前都能做出来
结果学的越多想的越复杂了

题目地址:【杭电】[5660]jrMz and angles