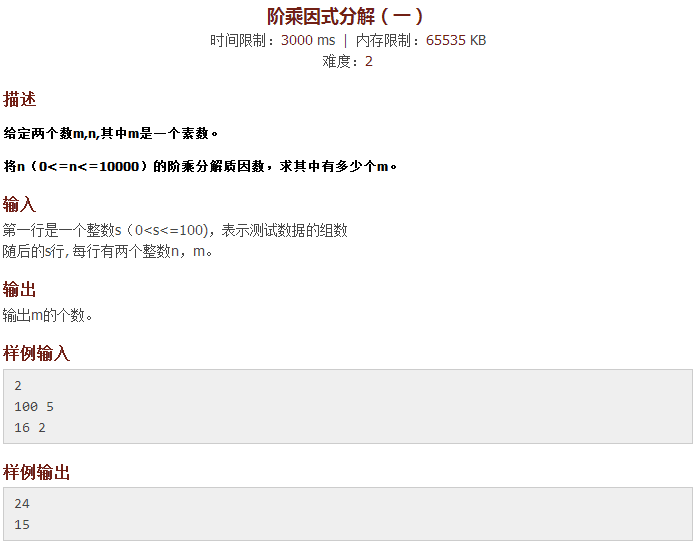
题目细想之下并不难
不过在
for(int k=i; !(k%m); cnt++)
循环的中止判定时
注意循环体执行的第一次前就会判定条件
如果不满足 则循环体一遍也会执行
注意 do-while是先循环一次再判断条件
探究:
【看书】for,(do-)while的循环体执行
所以这一题的思路就很简单了
n的阶乘为 1×2×3×4×……n
所以需要找其分解质因数
只需要判断 m~n 各有几个质因数
(比m小的分解肯定没有质因数是m)
判断一个数有几个质因数是 m
只需要把这个数不断除去m
知道无法整除 看除了多少次
AC代码:
#include<stdio.h>
int main() {
int T;
scanf("%d",&T);
while(T--) {
int m,n;
int i,cnt;
scanf("%d %d",&n,&m);
for(i=m,cnt=0; i<=n; i++)
for(int k=i; !(k%m); cnt++)
k/=m;
//循环体执行前先判断条件 注意和do-while的区别
printf("%d
",cnt);
}
return 0;
}标程则用了递归函数
还是涉及到了函数+表达式的形式
并且使用了另外一种思路
找到的一篇关于此的介绍文章
《阶乘因式分解 - sead+》
给定两个数m,n
求m!分解质因数后因子n的个数。
这道题涉及到了大数问题,如果相乘直接求的话会超出数据类型的范围。
下面给出一种效率比较高的算法,我们一步一步来。
m!=1*2*3*……(m-2)(m-1)*m
可以表示成所有和n倍数有关的乘积再乘以其他和n没有关系的
=(n*2n*3n*……*kn)*ohter other是不含n因子的数的乘积 因为 kn<=m 而k肯定是最大值 所以k=m/n
=n^k*(1*2*……*k)*other
=n^k*k!*other
从这个表达式中可以提取出k个n,然后按照相同的方法循环下去可以求出k!中因子n的个数。
每次求出n的个数的和就是m!中因子n的总个数。
这一种思路的实现是通过把n!的阶乘分解来实现的
例如 求 n=8 m=2 的结果
则
8!=24×4!×other (other代表剩余其它的数字)
那么
4!=22×2!×other
2!=21×1
所以 8! 里应该有4+2+1=7个2
同样的
对于 n=7 m=2 的结果
则
7!=23×3!×other (other=>7×5×3)
3!=21×1!×other (other=>3)
所以
7!里有3+1=4个2
这种运算方法无疑比直接找的算法更为简便
这也就是学算法的意义吧~
而标程的递归使得这一运算表达更加简明
#include<iostream>
using namespace std;
int get(int n,int num)
{
if(n==0) return 0;
else return get(n/num,num)+n/num;
}
int main()
{
int n;
cin>>n;
while(n--)
{
int a,b;
cin>>a>>b;
cout<<get(a,b)<<endl;
}
}题目地址:【NYOJ】[56]阶乘因式分解(一)
参考文章:
阶乘因式分解 - sead+