深度优先(DFS)
深度优先遍历,从初始访问结点出发,我们知道初始访问结点可能有多个邻接结点,深度优先遍历的策略就是首先访问第一个邻接结点,然后再以这个被访问的邻接结点作为初始结点,访问它的第一个邻接结点。总结起来可以这样说:每次都在访问完当前结点后首先访问当前结点的第一个邻接结点。
我们从这里可以看到,这样的访问策略是优先往纵向挖掘深入,而不是对一个结点的所有邻接结点进行横向访问。
算法大概过程:
1.把整个图的结构用矩阵来表示,如图:
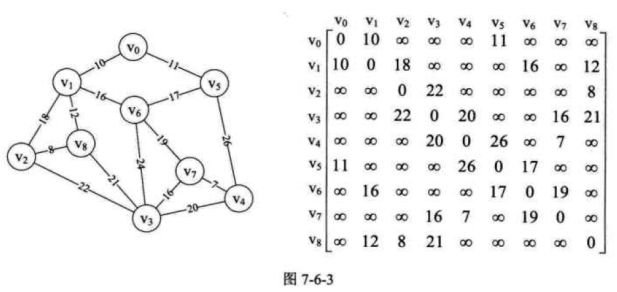
2.我们从第一个顶点(v0)开始遍历,拿到第一个邻接点(二维矩阵里是v1),这个时候我们再对v1进行遍历,v0已经被访问过了所以选择跳过,这时再拿到v2,对v2开始进行遍历。。。以此类推!
代码实现如下:
// 获取某顶点的第一个邻接点
private int getFirstNeighbor(int index) {
for (int i = 0; i < vertexSize; i++) {
if (matrix[index][i] > 0 && matrix[index][i] < MAX_WEIGHT) {
// 找到了第一邻接点
return i;
}
}
return -1;
}
// 根据前一个邻接点下标,来取得下一个邻接点
/**
* @param v1
* 表示要找的顶点
* @param index
* 表示该顶点相对于哪个邻接点去获取下一个邻接点
* @return
*/
private int getNextNeighbor(int v1, int index) {
for (int i = index + 1; i < vertexSize; i++) {
if (matrix[v1][i] > 0 && matrix[v1][i] < MAX_WEIGHT) {
return i;
}
}
return -1;
}
private void depthSearch(int i) {
isVisited[i] = true;// 证明当前顶点被访问过了
// 获取当前顶点的邻接点
int w = getFirstNeighbor(i);
// 只要w不是-1
while (w != -1) {
// 证明i确实有邻接点
// 判断w是否被访问过
if (!isVisited[w]) {
// 如果没有被访问过,就继续深度遍历w顶点
System.out.println("深度优先访问到的顶点:" + w);
depthSearch(w);
}
// 如果当前邻接点被访问过了,就继续搜索除了这个w外其他的点
w = getNextNeighbor(i, w);
}
}
public void depthFirstSearch() {
// 这是对外提供
isVisited = new boolean[vertexSize];
for (int i = 0; i < vertexSize; i++) {
if (!isVisited[i]) {
System.out.println("深度优先访问到的顶点:" + i);
depthSearch(i);
}
}
// 遍历完后,记得把布尔数组归为
isVisited = new boolean[vertexSize];
}
广度优先(BFS)
广度优先搜索类似于我们的二叉树的层次遍历,我们还是以v0作为起始点,根据二维矩阵,我们找到v0的第一个邻接点,之后再找到v0的第二个邻接点,直到找不到v0的邻接点为止,由图可知,v0就俩邻接点v1,v5。遍历完后,继续遍历v1的邻接点,v1的遍历完后,开始遍历v5的。。。以此类推!
代码如下:
// 广度优先遍历算法
public void broadFirstSearch() {
isVisited = new boolean[vertexSize];
for (int i = 0; i < vertexSize; i++) {
if (!isVisited[i]) {
System.out.println("广度优先访问到的顶点:" + i);
broadSearch(i);
}
}
isVisited = new boolean[vertexSize];
}
private void broadSearch(int i) {
// 类似于二叉树的层次遍历
int u, w;
LinkedList<Integer> queue = new LinkedList<>();
isVisited[i] = true;
queue.add(i);
while (!queue.isEmpty()) {
u = queue.removeFirst();// 顶点
w = getFirstNeighbor(u);
while (w != -1) {
if (!isVisited[w]) {
System.out.println("广度优先访问到的顶点:" + w);
isVisited[w] = true;
queue.add(w);
}
// 拿到后面的邻接点
w = getNextNeighbor(u, w);
}
}
}