优先队列——基于最大二叉堆的实现

一、二叉堆的定义

堆树的定义如下：

（1）堆是必须是一颗完全二叉树；

（2）堆中某个节点的值总是大于或者小于子节点的值；

（3）堆中每个非终端节点都可以看做是一个堆的根节点。

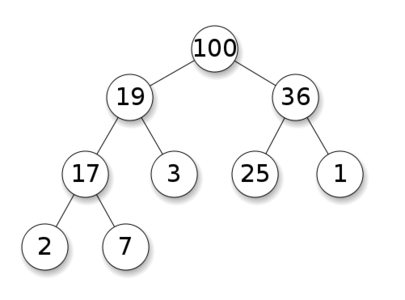
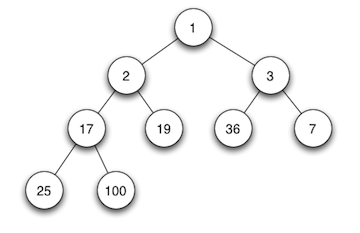
当父节点的键值总是大于或等于任何一个子节点的键值时为最大堆。 当父节点的键值总是小于或等于任何一个子节点的键值时为最小堆。如下图所示，左边为最大堆，右边为最小堆。

                                               

二、最大堆的操作

    原始数据为a[] = {4, 1, 3, 2, 16, 9, 10, 14, 8, 7}，采用顺序存储方式，对应的完全二叉树如下图所示：

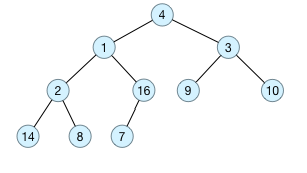
以上图的二叉树为例，我们来构造一个最大堆：

    首先，构造一个最大堆的思路就是：我们不需要从叶子节点开始遍历构造最大堆，因为叶子节点没有子节点，所以对叶子节点做构造大堆的过程是无效的，所以我们选择从最后一个叶子节点的父节点来开始从底层构造最大堆，一步步往上走，最终形成一整颗二叉树都是最大堆。

    而我们的最后一个叶子节点的父节点，它在数组对应的下标位置很特殊：（数组长度-1）/ 2，在上图中就是16这个元素

    而完全二叉树的中，如果父节点位置为i，那么左孩子是2i+1，右孩子是2i+2

    于是乎，我们要以16为第一个根节点，开始一步步构建最大堆！

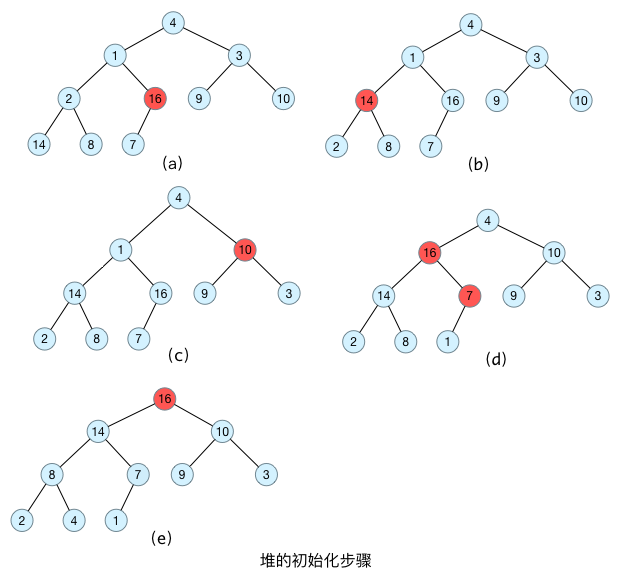
代码实现如下：

private Array<E> data;

	public MaxHeap(int capacity) {
		data = new Array<>(capacity);
	}

	public MaxHeap() {
		data = new Array<>();
	}

	public MaxHeap(E[] arr) {
		data = new Array<>(arr);
		// 建立一个大堆
		for (int i = parent(arr.length - 1); i >= 0; i--)
			siftDown(i);
	}

	// 返回堆中的元素个数
	public int size() {
		return data.getSize();
	}

	// 返回一个布尔值, 表示堆中是否为空
	public boolean isEmpty() {
		return data.isEmpty();
	}

	// 返回完全二叉树的数组表示中，一个索引所表示的元素的父亲节点的索引
	private int parent(int index) {
		if (index == 0)
			throw new IllegalArgumentException("index-0 doesn't have parent.");
		return (index - 1) / 2;
	}

	// 返回完全二叉树的数组表示中，一个索引所表示的元素的左孩子节点的索引
	private int leftChild(int index) {
		return index * 2 + 1;
	}

	// 返回完全二叉树的数组表示中，一个索引所表示的元素的右孩子节点的索引
	private int rightChild(int index) {
		return index * 2 + 2;
	}

	// 向堆中添加元素
	public void add(E e) {
		data.addLast(e);
		// 如果最后一个元素很大，需要上浮，因为这是大堆
		siftUp(data.getSize() - 1);// 把最后一个元素上浮
	}

	private void siftUp(int i) {
		while (i > 0/* 数组超过一个元素 */
				&& data.get(parent(i)).compareTo(data.get(i)) < 0) {
			data.swap(i, parent(i));
			i = parent(i);
		}
	}

	// 看堆中的最大元素
	public E findMax() {
		if (data.getSize() == 0)
			throw new IllegalArgumentException(
					"Can not findMax when heap is empty.");
		return data.get(0);
	}

	// 取出堆中最大元素
	public E extractMax() {

		E ret = findMax();

		data.swap(0, data.getSize() - 1);// 第一个最大元素和最后一个元素交换
		data.removeLast();
		siftDown(0);// 把第一个元素下沉

		return ret;
	}

	private void siftDown(int k) {
		// 沉淀
		while (leftChild(k) < data.getSize()) {
			int next = leftChild(k);
			if (next + 1 < data.getSize()
					&& data.get(next + 1).compareTo(data.get(next)) > 0) {
				// 我们选择右边的节点
				next++;
			}
			if (data.get(k).compareTo(data.get(next)) > 0) {
				// 如果父节点大于子节点，符合大堆，直接退出
				break;
			}
			// 否则选择左边的
			data.swap(k, next);
			k = next;
		}
	}

	// 取出堆中的最大元素，并且替换成元素e
	public E replace(E e) {

		E ret = findMax();
		data.set(0, e);
		siftDown(0);
		return ret;
	}

　　一个最大堆的实现在上面已经完成了！那么，我们的优先队列又是怎么一回事呢？？

       优先队列，顾名思义就是在一个队列中，并不是遵循的先进先出的原则，而是遵循的是看看添加的元素的优先级是怎样的

      例如，我添加了1,2,3元素，此时我添加进来4元素（这里的优先级准则是依据数字的大小），那么此时的4才应该替换之前的顶点（之前的是3），这时头结点是4，此时我们优先级最高的4确实是移到了最顶点。

      那么，我们的优先队列就可以基于上面我们已经实现的最大堆，来构建一个优先队列！

      代码如下所示：

 

public class PriorityQueue<E extends Comparable<E>> implements Queue<E> {

	private MaxHeap<E> maxHeap;

	public PriorityQueue() {
		maxHeap = new MaxHeap<>();
	}

	@Override
	public int getSize() {
		return maxHeap.size();
	}

	@Override
	public boolean isEmpty() {
		return maxHeap.isEmpty();
	}

	@Override
	public E getFront() {
		return maxHeap.findMax();
	}

	@Override
	public void enqueue(E e) {
		maxHeap.add(e);
	}

	@Override
	public E dequeue() {
		return maxHeap.extractMax();
	}
}