LeetCode687----最长同值路径

给定一个二叉树，找到最长的路径，这个路径中的每个节点具有相同值。 这条路径可以经过也可以不经过根节点。

注意：两个节点之间的路径长度由它们之间的边数表示。

示例 1:

输入:

              5
             / 
            4   5
           /    
          1   1   5

输出:

2

示例 2:

输入:

              1
             / 
            4   5
           /    
          4   4   5

输出:

2

注意: 给定的二叉树不超过10000个结点。 树的高度不超过1000。

思路：我们可以通过树结构发现，我们的每一个不同的同值路径（例如同值为2，或者同值为3），他们之间都是互不影响的，每次从一个同值路径跳到另一个同值路径时，前一个同值路径的状态不会影响到后一个同值路径：

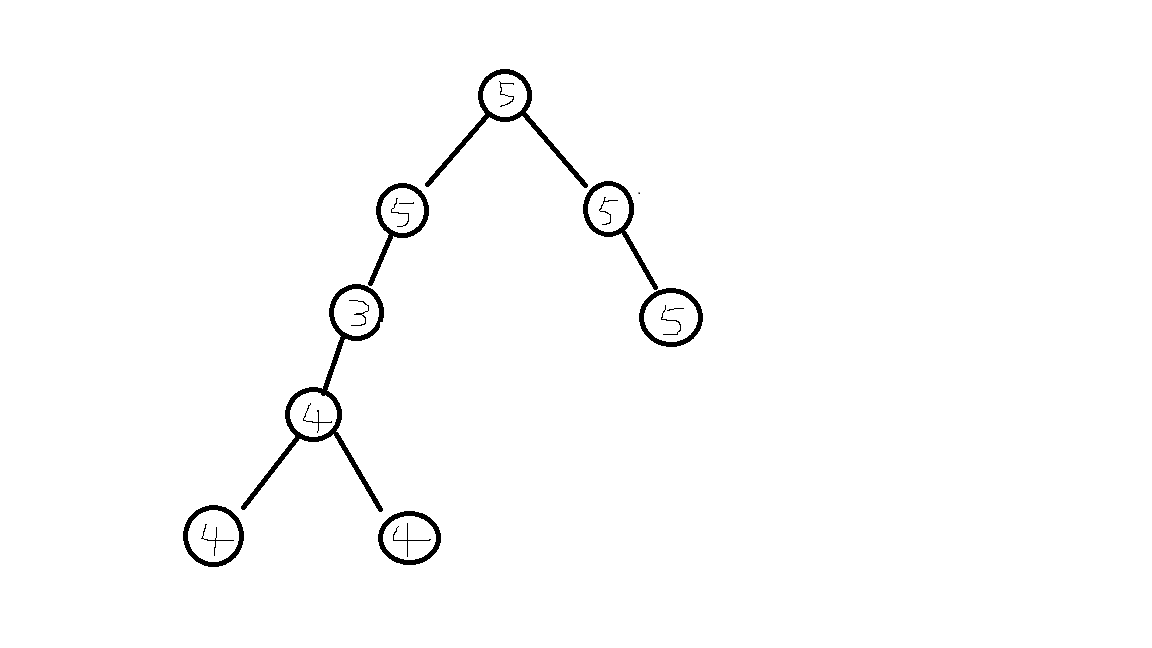
当同值为4的路径走到3时，这时就应该断开4的状态，一切从0开始，直到同值为5的路径开始，于是乎上图我们又可以这样来画！

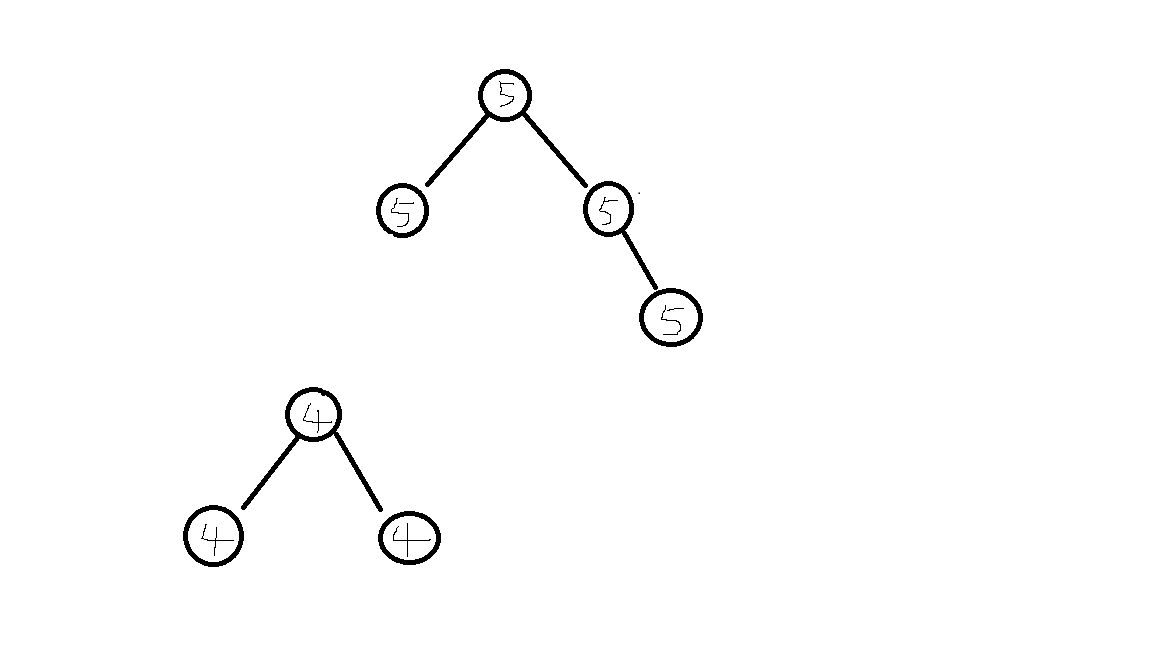
既然状态会断开，那么这里的3我们可以默认省去，这样，程序不论是走到最左下角的4节点还是最左下角的5节点，默认返回给其父节点的都是0

代码如下：

class Solution {
    public int max;
    
    public int longestUnivaluePath(TreeNode root) {
		help(root);
		return max;
	}

	public int help(TreeNode root) {
		if (root == null) {
			return 0;
		}
		int l = help(root.left);// 得到左边最大的路径
		int r = help(root.right);// 得到右边最大的路径
        int left = 0,right = 0;
		if (root.left != null && root.val == root.left.val) {
			// 证明根节点和当前的左子节点在一个路径
			left=l + 1;
		}
		if (root.right != null && root.val == root.right.val) {
			right=r + 1;
		}
		max = Math.max(max, left + right);
		return Math.max(left, right);
	}
}