Palindromic Matrix

Palindromic Matrix

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Let's call some square matrix with integer values in its cells palindromic if it doesn't change after the order of rows is reversed and it doesn't change after the order of columns is reversed.

For example, the following matrices are palindromic:

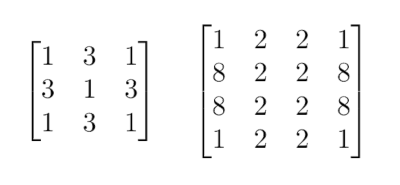
The following matrices are not palindromic because they change after the order of rows is reversed:

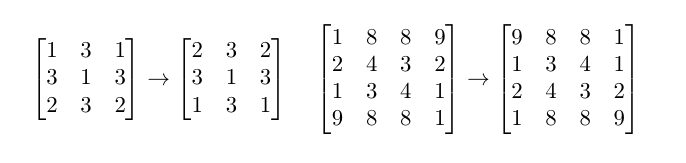
The following matrices are not palindromic because they change after the order of columns is reversed:

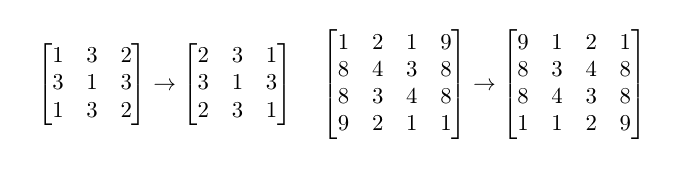
You are given n2n2 integers. Put them into a matrix of nn rows and nn columns so that each number is used exactly once, each cell contains exactly one number and the resulting matrix is palindromic. If there are multiple answers, print any. If there is no solution, print "NO".

Input

The first line contains one integer nn (1≤n≤201≤n≤20 ).

The second line contains n2n2 integers a1,a2,…,an2a1,a2,…,an2 (1≤ai≤10001≤ai≤1000 ) — the numbers to put into a matrix of nn rows and nn columns.

Output

If it is possible to put all of the n2n2 numbers into a matrix of nn rows and nn columns so that each number is used exactly once, each cell contains exactly one number and the resulting matrix is palindromic, then print "YES". Then print nn lines with nn space-separated numbers — the resulting matrix.

If it's impossible to construct any matrix, then print "NO".

You can print each letter in any case (upper or lower). For example, "YeS", "no" and "yES" are all acceptable.

Examples

Input

Copy

4
1 8 8 1 2 2 2 2 2 2 2 2 1 8 8 1

Output

Copy

YES
1 2 2 1
8 2 2 8
8 2 2 8
1 2 2 1

Input

Copy

3
1 1 1 1 1 3 3 3 3

Output

Copy

YES
1 3 1
3 1 3
1 3 1

Input

Copy

4
1 2 1 9 8 4 3 8 8 3 4 8 9 2 1 1

Output

Copy

NO

Input

Copy

1
10

Output

Copy

YES
10 

#include<iostream>
#include<cstring>
#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;

#define forn(i,n) for( int i=0; i<n; i++ )
typedef pair<int,int> pt;
const int maxn =10000+7;
int cnt[maxn];
int a[20][20];

int main(int argc, char const *argv[])
{
    int n;
    scanf("%d",&n);
    forn(i,n*n){
        int x;
        scanf("%d",&x);
        cnt[x]++;
    }
    vector<pair<int,pt> > cells;
    forn(i,(n+1)/2) forn(j,(n+1)/2){
        if(i!=n-i-1&&j!=n-j-1){
            cells.push_back({4,{i,j}});
        }
        else if((i!=n-i-1)^(j!=n-j-1)){
            cells.push_back({2,{i,j}});
        }
        else{
            cells.push_back({1,{i,j}});
        }
    }
    for( auto cur : {4,2,1}){
        int lst=1;
        for( auto it : cells ){
            if(it.first!=cur) continue;
            int i=it.second.first;
            int j=it.second.second;
            while(lst<maxn&&cnt[lst]<cur){
                lst++;
            }
            if(lst==maxn){
                puts("NO");
                return 0;
            }
            a[i][j]=a[n-i-1][j]=a[i][n-j-1]=a[n-i-1][n-j-1]=lst;
            cnt[lst]-=cur;
        }
    }
    puts("YES");
    forn(i,n){
        forn(j,n){
            printf("%d ",a[i][j]);
        }
        puts("");
    }
    return 0;
}