[CF494B] Obsessive String

Hamed has recently found a string t and suddenly became quite fond of it. He spent several days trying to find all occurrences of t in other strings he had. Finally he became tired and started thinking about the following problem. Given a string s how many ways are there to extract k ≥ 1 non-overlapping substrings from it such that each of them contains string t as a substring? More formally, you need to calculate the number of ways to choose two sequences a₁, a₂, ..., a_k and b₁, b₂, ..., b_k satisfying the following requirements:

• k ≥ 1
• 
• 
• 
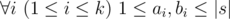
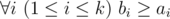
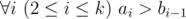
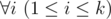•   t is a substring of string s_ais_ai + 1... s_bi (string s is considered as 1-indexed).

As the number of ways can be rather large print it modulo 10⁹ + 7.

Input

Input consists of two lines containing strings s and t (1 ≤ |s|, |t| ≤ 10⁵). Each string consists of lowercase Latin letters.

Output

Print the answer in a single line.

---

此题两种DP方式。

先预处理出来b串在a串中匹配的位置，然后开始DP。

设$f[i]$表示考虑到$i$位置，且$i$的最后一个字符串与b串是匹配的方案数。

显然如果$i$不是b的匹配位置，$f[i]=f[i-1]$。

如果$i$是b的匹配位置，首先考虑只有一个串, 那么答案就是$i-lb+1$，因为$1$到$i-lb+1$的所有位置都可以作为一个开始。

那如果是多个串呢？如果我们设最后一个串从位置$k$开始，那么前面的所有的方案数就是$large sum_{i=1}^{k}f[i]$，对于每个位置k求和，就是$large sum_{k=1}^{i-lb} sum_{j=1}^{k} f[j]$。

这样只用记录一下f的前缀和和f的前缀和的前缀和就可以快速转移啦。

代码在后面贴。

还有一种方法，状态的定义略微的有些不同，设$f[i]$表示，到第i个位置之前总共有多少方案，其实就是前缀和了一下。

每次记录上一个匹配点，从上一个匹配点开始转移。

代码贴后面了。

找匹配点可以用kmp，或者hash都行。

---

方法1：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
using namespace std;
#define reg register 
#define mod 1000000007
int la, lb;
char a[100005], b[100005];
unsigned long long hsha[100005], hshb[100005], fac[100005];
bool End[100005];
int f[100005], sum[100005], Ssum[100005];
int ans;

int main()
{
    scanf("%s%s", a + 1, b + 1);
    la = strlen(a + 1), lb = strlen(b + 1);
    for (reg int i = 1 ; i <= la ; i ++) hsha[i] = hsha[i - 1] * 27 + (a[i] - 'a' + 1);
    for (reg int i = 1 ; i <= lb ; i ++) hshb[i] = hshb[i - 1] * 27 + (b[i] - 'a' + 1); 
    fac[0] = 1;
    for (reg int i = 1 ; i <= max(la, lb) ; i ++) fac[i] = fac[i - 1] * 27;
    for (reg int i = lb ; i <= la ; i ++)
        if (hsha[i] - hsha[i - lb] * fac[lb] == hshb[lb]) End[i] = 1;
    for (reg int i = 1 ; i <= la ; i ++)
    {
        if (!End[i]) f[i] = f[i-1];
        else f[i] = Ssum[i - lb] + i - lb + 1;
        sum[i] = sum[i-1] + f[i];if(sum[i] >= mod) sum[i] -= mod;
        Ssum[i] = Ssum[i-1] + sum[i];if(Ssum[i] >= mod) Ssum[i] -= mod;
    }
    for (reg int i = 1 ; i <= la ; i ++)
        ans = (ans + f[i]) % mod;
    cout << ans << endl;
    return 0;
}

方法2：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
using namespace std;
#define reg register 
#define mod 1000000007
int la, lb;
char a[100005], b[100005];
int nxt[100005];
bool End[100005];
int f[100005], sum[100005];

int main()
{
    scanf("%s%s", a + 1, b + 1);
    la = strlen(a + 1), lb = strlen(b + 1);
    int k = 0;
    for (reg int i = 2 ; i <= lb ; i ++)
    {
        while(k and b[i] != b[k + 1]) k = nxt[k];
        if (b[k + 1] == b[i]) k ++;
        nxt[i] = k;
    }
    k = 0;
    for (reg int i = 1 ; i <= la ; i ++)
    {
        while(k and a[i] != b[k + 1]) k = nxt[k];
        if (b[k + 1] == a[i]) k ++;
        if (k == lb) End[i] = 1;
    }
    int lst = -1;
    for (reg int i = 1 ; i <= la ; i ++)
    {
        f[i] += f[i-1];
        if (End[i]) lst = i - lb + 1;
        if (lst != -1) f[i] += sum[lst - 1] + lst;
        if (f[i] >= mod) f[i] -= mod;
        sum[i] = sum[i-1] + f[i];
        if (sum[i] >= mod) sum[i] -= mod;
    }
    cout << f[la] << endl;
    return 0;
}