常见的排序算法——归并排序

一、基本思想

　　归并排序是建立在归并操作上的一种有效的排序算法，该算法是采用分治法（divide-and-conquer）的一个非常典型的应用。（分治法将问题分(divide)成一些小的问题然后递归求解，而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起，即分而治之)。

　　归并排序的步骤：

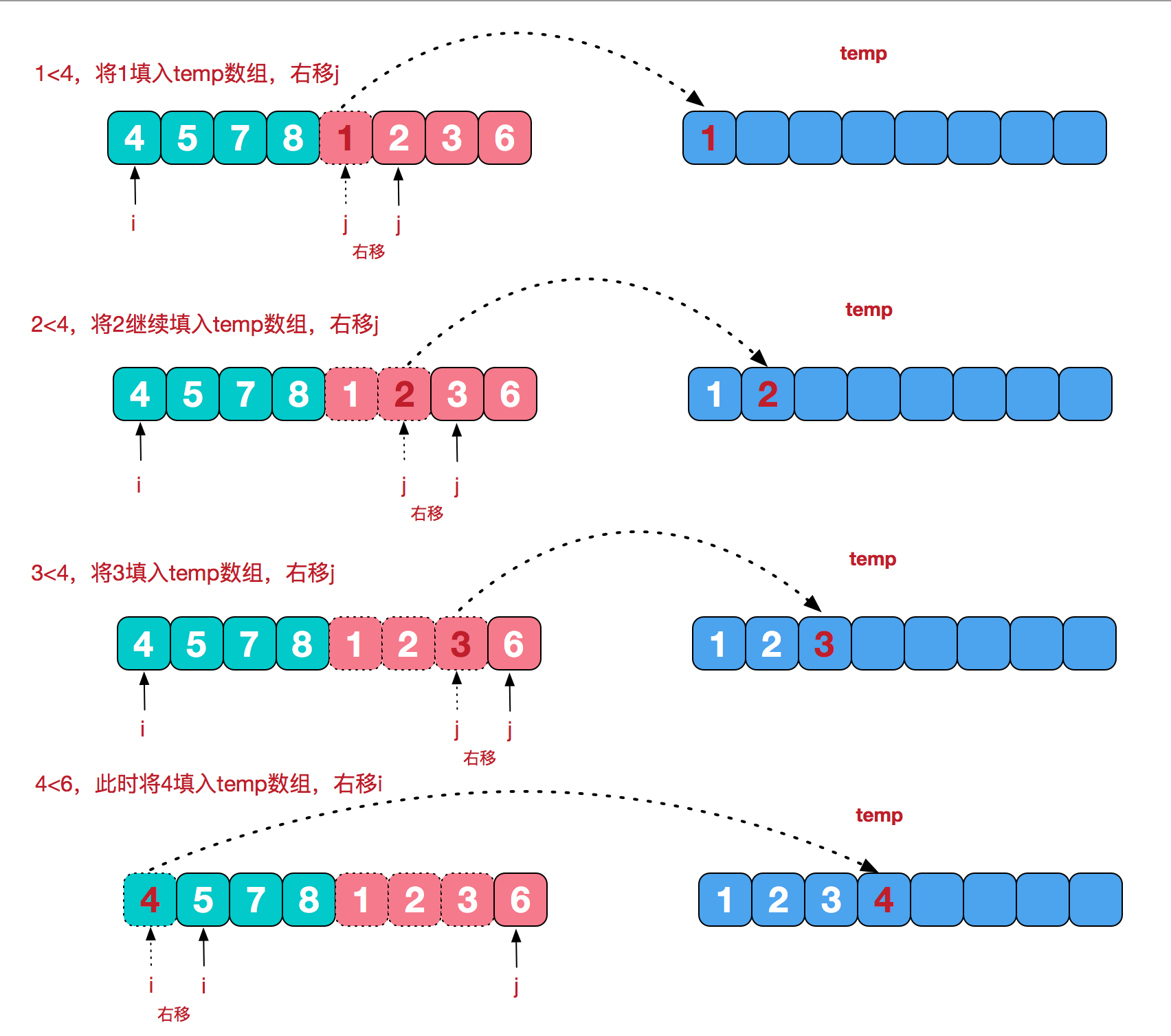
1. 申请空间，大小为两个已经排好序的序列之和，用来存放合并后的序列；
2. 设置两个指针，初始指向序列的起始位置；
3. 比较两个指针指向的元素，选择较小的元素放到合并空间，并移动指针到下一位置；
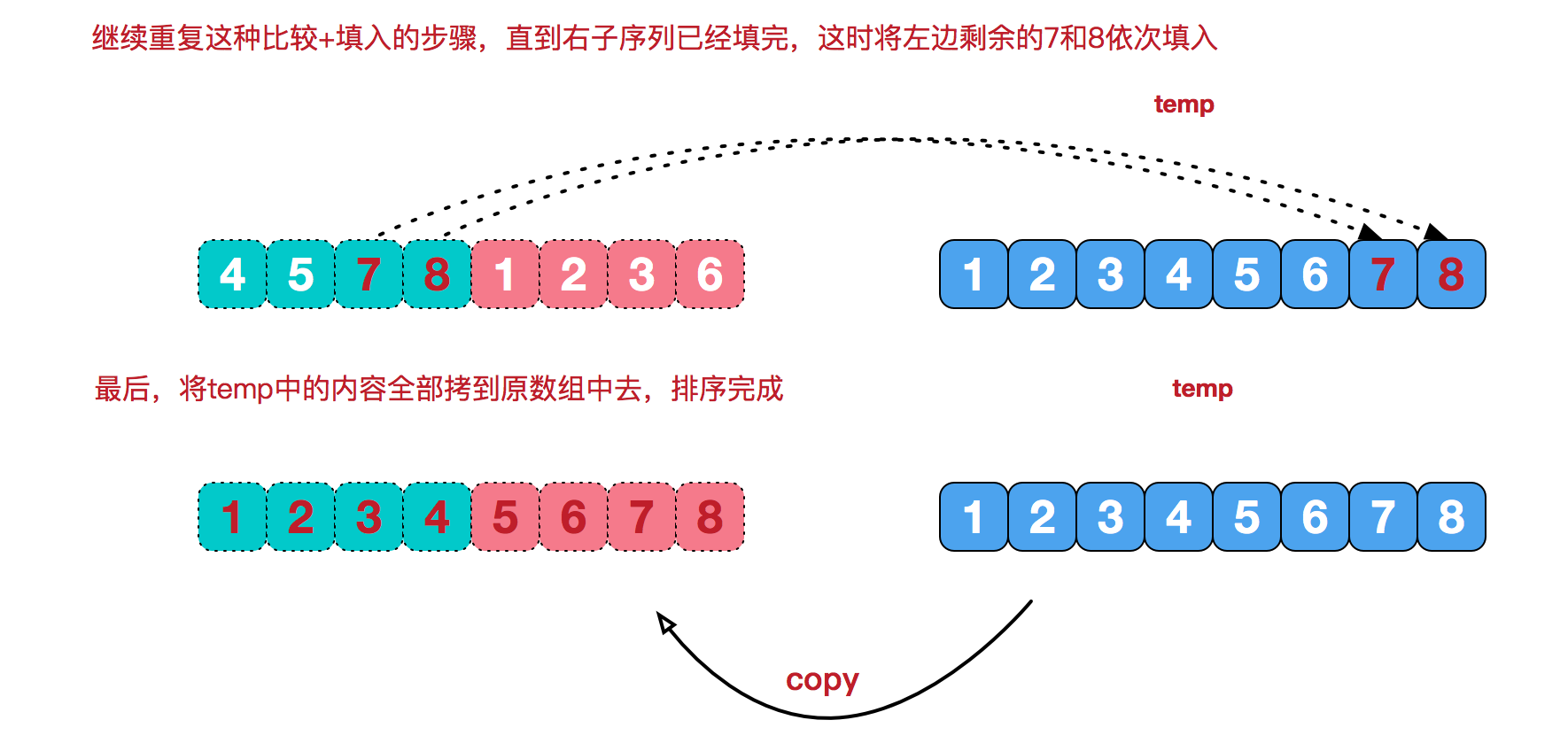
4. 重复步骤3直到某一指针到达序列尾，将另一序列剩下的元素复制到合并序列尾部；

分治过程图解：（参考 https://www.cnblogs.com/chengxiao/p/6194356.html）

合并步骤图解：

代码实现：

#include <iostream>
#include <vector>
using namespace std;

void PrintArray(vector<int>& vec)
{
    //for(int i = 0; i < vec.size(); i++)
    //    cout << vec[i]  << " " ;
    //cout << endl;
    
    vector<int>::iterator it;
    for(it = vec.begin(); it != vec.end(); it++)    
        cout << *it << " ";    
    cout << endl;
}

void merge(vector<int>& vec, int start, int mid, int end)
{
    int n = end - start + 1;
    if(n>0)
    {
        int k = 0;
        int i = start, j = mid + 1;
        int tmp[n] = {0};
        
        while(i <= mid && j <= end)
        {
            if(vec[i] < vec[j])
                tmp[k++] = vec[i++];
            else
                tmp[k++] = vec[j++];                
        }
        while(i <= mid)
        {
            tmp[k++] = vec[i++];
        }
        while(j <= end)
        {
            tmp[k++] = vec[j++];        
        }
        k = 0;
        while(start <= end)
        {
            vec[start++] = tmp[k++];
        }
    }
}

void merge_sort(vector<int>& vec, int start, int end)
{
    if(start < end)
    {
        int mid = (start + end)/2;
        merge_sort(vec, start, mid);        //这里是一步步的分开
        merge_sort(vec, mid+1, end);
        merge(vec, start, mid, end);        //这里是一步步的合并
    }
}


int main()
{    
    vector<int> vec;
    for(int i = 9; i > 0; i--)
        vec.push_back(i);
    cout << "input  :" << endl; 
    PrintArray(vec);
    merge_sort(vec, 0, 8);
    cout << "sort over  :" << endl; 
    PrintArray(vec);

    return 0;
}

说明：

　　归并排序是稳定排序，每次合并操作的时间复杂度是O(n)，深度是logn，所以总的时间复杂度是O(nlogn)。并且最好=最坏=平均时间复杂度都是O(nlogn)

　　空间复杂度：需要额外大小一样的辅助空间，所以空间复杂度是O(n)。