洛谷P2822:https://www.luogu.org/problemnew/show/P2822
思路
由于n和m都多达2000
所以暴力肯定是会WA的
因为整个组合数是不会变的
所以我们想到存下这个组合数(杨辉三角)阵型
注意要用二维前缀和存下 后来的k次询问就可以用O(1)解答
关于二维前缀和
用此图可以解答:
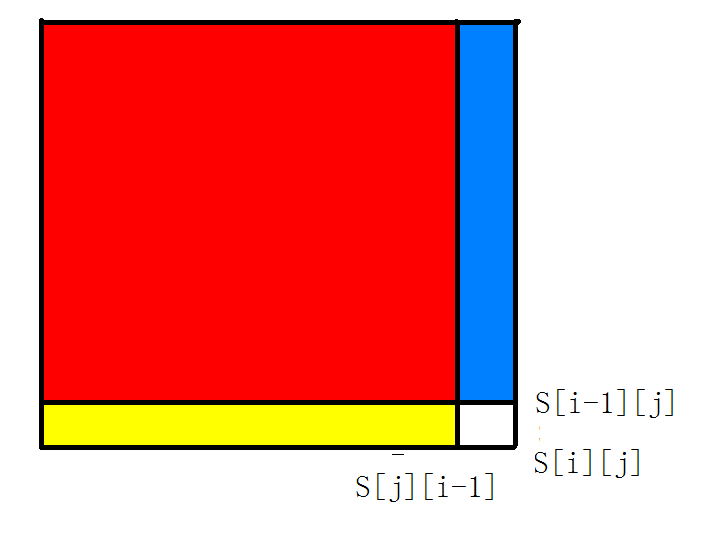
关键代码:s[i][j]=s[i][j-1]+s[i-1][j]-s[i-1][j-1];
来自dalao的口诀:上加左 减左上 加自己
代码

#include<iostream> using namespace std; #define maxn 2005 int c[maxn][maxn],s[maxn][maxn]; int t,k,m,n; void build() { for(int i=1;i<=2000;i++) { c[i][0]=c[i][i]=1; for(int j=1;j<=i-1;j++) c[i][j]=(c[i-1][j-1]+c[i-1][j])%k;//杨辉三角递推 } for(int i=2;i<=2000;i++) { for(int j=1;j<=i;j++) { s[i][j]=s[i][j-1]+s[i-1][j]-s[i-1][j-1]; if(!c[i][j])//如果c[i][j]为0说明 它是k的倍数 s[i][j]+=1;//ans加1 } s[i][i+1]=s[i][i];//详见后文注释<1> } } int main() { cin>>t>>k; build(); while(t) { t--; cin>>n>>m; if(m>n) m=n;//m不能大于n cout<<s[n][m]<<endl; } }
注释<1>:
补齐杨辉三角的右上角一排 否则二维前缀和在最右边无法算出
对于k=2
例: 1 0 0 如果不加这句代码 0
1 1 0 0 0 0 0
1 2 1 0 1 1 1 0 1 0
1 3 3 1 0 1 1 1 1 0 1 0 0
对于最右边的一排1的位置的前缀和无法计算 因为没有上面的值
