当我们使用回溯思想的算法,需要 dfs 解空间树从而得到问题的解。当我构造的解空间树形状为子集树时,我遇到了一个问题,为什么上界函数只在树的不使当前解增大的一侧上进行剪枝呢?举个例子,当利用回溯法(构造子集树)解决一维01背包问题的时候,上界函数只对子集树的不放当前第 i 号物品的子树进行剪枝。
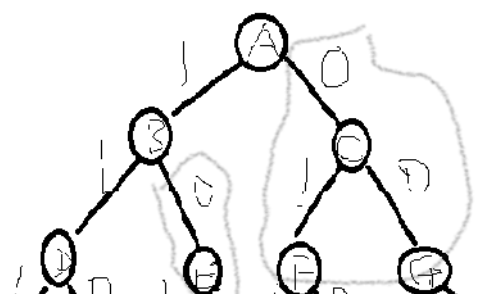
e.g. 三个物品时构建的解空间树,灰色圈内代表的是需要利用上界函数 bound 进行剪枝判断的子树
我们先来看看为什么进入左子树时不需要计算上界。在01背包问题中,由于进入左子树执行的是“增”操作,所以左子树的未选物品的重量与已选物品的重量之和与其父结点的未选物品的重量与已选物品的重量之和是相同的,其上界不变,所以不需要利用上界判断是否剪枝。
而在进入右子树时,由于它执行的是“减”操作,所以需要利用上界函数判断是否剪枝。你可能会疑惑,哪里减了,不就是不选第 i 个物品吗?非也,此时未选中物品的重量已经下降,而已选中物品的重量之和是不变的,那么它们二者总和其实是下降的了。所以此时它的上界相对于父节点是降低了,需要利用上界函数判断有没有必要往下走。
再拿一道经典问题——双船装载问题,来说明一下这个技巧。
描述: 有两艘船,载重量分别是c1、 c2,n个集装箱,重量是wi (i=1…n),且所有集装箱的总重量不超过c1+c2。确定是否有可能将所有集装箱全部装入两艘船。 输入: 多个测例,每个测例的输入占两行。第一行一次是c1、c2和n(n<=10);第二行n个整数表示wi (i=1…n)。n等于0标志输入结束。 输出: 对于每个测例在单独的一行内输出Yes或No。 输入样例: 7 8 2 8 7 7 9 2 8 8 0 0 0 输出样例: Yes No
双船问题实际上是一个最大子集和问题,求所有货物的重量与第一艘船载重最接近的一个划分,然后再看剩下货物的重量是否能被第二艘船装下。
可以发现实际和一维01背包是一样的套路,进入右子树后实际执行的是“减”操作,未上船的物品重量与已上船的物品重量之和实际是减少了,和父节点的上界已经不一样,更得更小了,所以需要利用上界函数判断是否需要剪枝。
下面是我的解题思路,代码只贴出了变量定义+构造子集树进行回溯:
#include <iostream> #include <cstdio> #include <cstdlib> #include <cstring> #include <algorithm> #include <vector> using namespace std; int n;//集装箱数 int w[1000];//集装箱重量 bool x[1000];//船1关于选择集装箱的解向量 int c1,c2;//两艘船的载重量 int curw;//当前载重量 int bestw;//当前最优载重量 int r;//剩余集装箱重量 void backtrack(const int& i) { if (i > n) { if (curw > bestw) { bestw = curw; } return; } r -= w[i]; //记录剩余集装箱重量的目的是为了使用上界函数进行剪枝 //可行性约束函数,考虑集装箱比整艘船的总容量还大的情况 //进左枝,以搜索当前最优解且保存bestw以剪枝 if ( w[i] + curw <= c1 ) { x[i] = true; curw += w[i]; backtrack(i+1); } //减枝函数(上界函数),r+ c1 <= bestw 时进行剪枝,停止递归 //减右枝(集装箱不上船的情况,通过best判断) if (r + curw > bestw) backtrack(i+1); r += w[i]; } int main() { FILE *fin = fopen("in.txt", "rb"); FILE *fout = fopen("out.txt", "wb"); while (fscanf(fin, "%d %d %d", &n, &c1, &c2) == 3) { //cin>> n >> c1 >> c2; int i = 1; int sum = 0; memset(w, 0, sizeof(w)); //集装箱总重量 while(i <= n) { cin >> w[i]; r += w[i]; sum += w[i]; i++; } backtrack(1); backtrack(1); if((bestw > 0) && ((sum - bestw) <= c2)) { fprintf(fout, "Yes "); //cout << "Yes" << endla; std::vector<int> x_c1, x_c2; for (int j = 1; j <= n; j++) { if(x[j] == true) x_c1.push_back(j); else x_c2.push_back(j); } cout << "轮船1装载的重量为:" << bestw << "轮船2装载的重量为:"<< sum-bestw << endl; cout << "轮船1装载的货物是:" ; for (size_t i = 0; i < x_c1.size(); i++) cout << x_c1[i] << " "; cout << endl; cout << "轮船2装载的货物是:"; for (size_t i = 0; i < x_c2.size(); i++) cout << x_c2[i] << " "; cout << endl; } else fprintf(fout, "Not "); } fclose(fin); fclose(fout); return 0; }