二叉树的遍历--递归实现与非递归实现

二叉树的表示

在研究二叉树的遍历之前，我们需要先看看二叉树的表示方式。

一般来说，我们使用自定义的数据结构或是数组来表示二叉树。

• 二叉树的数据结构：

public class TreeNode {
    public int val;
    // 左孩子
    public TreeNode left;
    // 右孩子
    public TreeNode right;
}

• 数组形式表现二叉树

  当我们使用数组形式表现二叉树时，我们将数组第一个节点的索引置为「1」，也就是根节点，如果我们通用性的将其当为「x」，那么它的左孩子节点的索引就是「2*x」，右孩子节点的索引为「2*x+1」。

  例如下面的二叉树，我们可以使用数组[null, 1, 2, 3, null, 4, 5]来表示（因为根节点的索引需要为1，因此数组第一个元素我们将其置为null）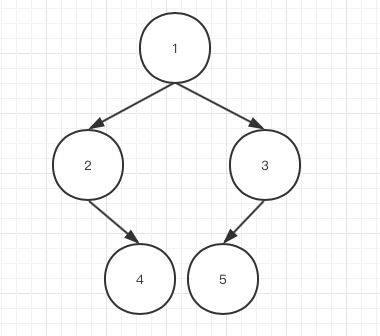

  

二叉树的遍历

二叉树中一般有四种遍历方式：前序遍历、中序遍历、后序遍历和层序遍历。它们都可以通过「递归」或是「非递归」实现，递归便于理解但是效率低下且不安全，可能会出现栈溢出；非递归，即采用循环，通常采用栈来完成，会复杂一些，但能够提高效率，降低遍历的消耗。其中『层序遍历』本质上是图的「广度优先搜索」，与另外三种有较大差异，故我们这里只讨论前序、中序和后序遍历方式，层序遍历放在之后进行讨论。

在下面的实现中，我们用一个名为「result」的队列来模拟遍历的顺序

前序遍历

访问顺序：根 → 左 → 右

递归实现

public class PreorderTraversal {
    public List<Integer> preorderTraversal(TreeNode root) {
        //add()和remove()方法在失败的时候会抛出异常(不推荐),应使用add()和poll()代替
        List<Integer> result = new LinkedList<>();
        // 进行前序遍历
        _preorderTraversal(root, result);
        return result;
    }

    private void _preorderTraversal(TreeNode node, List<Integer> result) {
        if (null != node) {
            // 先输出根节点的值，然后再顺序处理左孩子和右孩子
            result.add(node.val);
            _preorderTraversal(node.left, result);
            _preorderTraversal(node.right, result);
        }
    }
}

非递归实现

实现思路

非递归实现时前序遍历时，我们需要借助栈(Stack)这一数据结构来完成，根据前序遍历「根-左-右」的特点，我们用以下思路来解决：

• 预处理：将根节点 push 到栈中

• 通过循环遍历树：

  1. 检测栈是否为空，空则结束循环；若非空，则 pop 栈顶元素，并输出栈顶元素的值

  2. 判断栈顶元素「右孩子」是否为 null，非空则将其 push 到栈中

  3. 判断栈顶元素「左孩子」是否为 null，非空则将其 push 到栈中

在上面思路中，因为栈这一数据结构是「先进后出」的，所以我们先压入右孩子，后压入左孩子，这样最终访问时能够先访问左孩子。

参考代码

这里对于前序、中序和后序遍历的非递归实现，都会给出两种代码，第一种代码较为直观，易于理解；第二种代码属于模版类型的代码，形式统一，便于记忆。

这里先给出符合上述思路，便于理解的代码

public class PreorderTraversal {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new LinkedList<>();
        // 1. 将根节点push到栈
        Stack<TreeNode> tempStack = new Stack<>();
        tempStack.push(root);
        // 2. 通过循环遍历树
        while (!tempStack.empty()) {
            TreeNode node = tempStack.pop();
            result.add(node.val)
            if (null != node.right) {
                tempStack.push(node.right);
            }
            if (null != node.left) {
                tempStack.push(node.left);
            }
        }
        return result;
    }
}

便于记忆的模版代码

这里为什么给出模版代码？

因为二叉树这东西，看着思路理解很快，但是实际写起来容易忘这忘那，所以这里给出模版代码，我们可以多看几遍模版代码先记下如何使用，在熟练之后就可以得心应手的使用二叉树了。

模版代码的思路

• 预处理

  在遍历二叉树的模版中，我们需要引入一个『辅助节点 curr』保存「当前正在访问的节点」，初始化为根节点，保证栈顶元素始终是 curr 的根节点；每次循环时判断条件为当前栈非空或辅助节点 curr 不为空。

• 使用循环前序遍历二叉树

  对于这个模版，我们要牢记其在循环中的两种情况，这是根据辅助节点 curr 是否为null进行判断的

  1. curr 存在时，表示栈顶元素存在左孩子，将 curr 压入栈并输出 curr 的值，最后将 curr 节点的值指向其左孩子节点

  2. 如果 curr 为空(即不存在)，表示栈顶的节点不存在左子树，这是我们弹出栈顶的节点，将 curr 指向被弹出栈顶节点的右孩子节点

模版代码

public class PreorderTraversal {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new LinkedList<>();

        // 1. 初始化辅助节点curr
        Stack<TreeNode> tempStack = new Stack<>();
        TreeNode curr = root;

        // 2. 通过循环遍历树
        while (!tempStack.empty() || null != curr) {
            if (null != curr) {
                tempStack.push(curr);
                result.add(curr.val);
                curr = curr.left;
            }
            if (null == curr) {
                // 如果下一次循环中 curr 也为空，则表示对于本次弹出后的栈，其栈顶节点左子树已经遍历完毕了，仍然是弹出栈顶节点并对其右子树遍历
                curr = tempStack.pop().right;
            }
        }
        return result;
    }
}

中序遍历

访问顺序：左 → 根 → 右

递归实现

递归代码和前序遍历类似，只是这里我们需要先递归访问到整棵树的最左叶节点

public class InorderTraversal {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new LinkedList<>();
        _inorderTraversal(root, result);
        return result;
    }

    private void _inorderTraversal(TreeNode node, List<Integer> result) {
        if (null != node) {
            _inorderTraversal(node.left, result);
            // 输出完左孩子就输出根节点，之后再处理右孩子
            result.add(node.val);
            _inorderTraversal(node.right, result);
        }
    }
}

非递归实现

实现思路

同样的，我们使用栈(Stack)来实现树的中序遍历，我们需要牢记中序遍历的顺序是「左-根-右」。也就是在打印当前节点之前，要保证该节点的左子树不存在或已经遍历完毕，所以我们同样需要一个『辅助节点 curr』来保存「正在访问的节点信息」，在循环开始时保证它指向栈顶节点的左孩子，在 curr 为null时我们便认为栈顶元素的左子树已无需遍历, 而循环跳出条件也需要变成当前栈非空或 curr 非空。

• 预处理：将辅助节点 curr 初始化为根节点

• 通过循环遍历树

  1. 将当前节点 curr 的所有左孩子节点压入栈

  2. 弹出栈顶的元素，让 curr 指向该元素并输出

  3. 让当前节点 curr 指向其自身的右孩子

参考代码

public class InorderTraversal {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new LinkedList<>();

        Stack<TreeNode> tempStack = new Stack<>();
        TreeNode curr = root;

        while (null != curr || !tempStack.empty()) {
            while (null != curr) {
                tempStack.push(curr);
                curr = curr.left;
            }
            // 此时可以保证栈顶元素不存在左子树，弹出并输出，最后再对其右孩子节点进行迭代判定
            curr = tempStack.pop();
            result.add(curr.val);
            curr = curr.right;
        }

        return result;
    }
}

便于记忆的模版代码

实现思路

• 预处理：将辅助节点初始化为根节点

• 通过循环实现遍历

  既然是模版，那么形式上和之前前序遍历的模版是类似的，不同的仅是对于辅助节点 curr 是否为null的两种情况的处理：

  1. 当前节点curr 存在，此时将 curr 压入栈之后仅让 curr 指向其左孩子

  2. 当前节点curr 为null，此时栈顶元素的左子树为空，我们将栈顶元素弹出并输出，然后让当前节点 curr 指向其右孩子

模版代码

public class InorderTraversal {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new LinkedList<>();

        Stack<TreeNode> tempStack = new Stack<>();
        TreeNode curr = root;

        while (null != curr || !tempStack.empty()) {
            if (null != curr) {
                tempStack.push(curr);
                curr = curr.left;
            }
            if (null == curr) {
                curr = tempStack.pop();
                result.add(curr.val);
                // 如果当前节点curr是叶子节点，则curr的右孩子一定为null，下次循环时会再次弹出栈顶元素(也就是当前访问节点curr的根节点)进行输出
                curr = curr.right;
            }
        }
        return result;
    }
}

后序遍历

访问顺序：左 → 右 → 根

递归实现

在后序遍历时，我们需要先访问整棵树的最左子节点，再访问与这个最左子节点根节点的右节点

参考代码

public class postorderTraversal {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> result = new LinkedList<>();
        _postorderTraversal(root, result);
        return result;
    }

    private void _postorderTraversal(TreeNode node, List<Integer> result) {
        if (null != node) {
            _postorderTraversal(node.left, result);
            _postorderTraversal(node.right, result);
            // 输出了左孩子和右孩子之后，才输出根节点
            result.add(node.val);
        }
    }
}

非递归实现

实现思路

后序遍历的非递归实现依然依靠栈(Stack)实现，这里它的遍历顺序是「左-右-根」。类似于中序遍历要保证当前节点的左子树已无需遍历，对于后序遍历，我们输出一个节点之前，要保证它的左子树和右子树都已经无需遍历。

在之前的中序遍历，我们使用『curr』表示当前节点，并令其起到判断当前栈顶元素的左子树是否需要遍历的作用(即判断 curr 是否为null)；而后序遍历我们还要保证右子树是否被遍历，因此我们这里再引入一个节点『right』表示「上次遍历的右节点」，帮助我们判断栈顶元素的右子树是否需要遍历。

参考代码

public class postorderTraversal {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> result = new LinkedList<>();
        Stack<TreeNode> tempStack = new Stack<>();
        TreeNode curr = root;
        TreeNode right = null;

        while (null != curr || !tempStack.empty()) {
            while (null != curr) {
                tempStack.push(curr);
                curr = curr.left;
            }
            // 这时可以保证栈顶元素的左子树为空或已被遍历了
            curr = tempStack.peek();
            // 遍历可能存在的右子树
            // 如果栈顶元素的右节点存在且未被访问，则需要先对其右节点进行遍历
            if (null != curr.right && curr.right != right) {
                curr = curr.right;
                right = null;
                continue;
            }
            // 此时，左、右子树均不存在或者被遍历过，则输出当前节点
            result.add(curr.val);
            // 弹出遍历过的元素
            tempStack.pop();
            // curr可能是栈顶元素的右孩子
            right = curr;
            // 将curr置为空保证下一次循环时直接取出栈顶元素(即这时curr的根元素)
            curr = null;
        }
        return result;
    }
}

便于记忆的模版代码

实现思路

我们知道后序遍历的顺序是「左-右-根」，再看一下之前前序遍历的顺序：「根-左-右」。在遍历时，我们将遍历结果顺序压入队列中，考虑如下两个操作：

1. 前序遍历时，我们将结果压入队列尾部；如果我们现在将每次遍历的结果压入队列头部，那么我们从队列中得到的顺序就变成了「右-左-根」

2. 在前序遍历时，为什么可以保证先访问左节点，再访问右节点？因为我们每次遍历时优先寻找当前节点的左孩子；如果我们现在每次遍历时，优先寻找右孩子，那么在『1』的基础上，队列中保存的顺序就变成了「左-右-根」，这就是后序遍历的顺序了。

在上述思路和前序遍历模版代码的基础上，我们可以知道代码的方式如下:

• 预处理：将辅助节点初始化为根节点，循环跳出条件依然是「当前节点curr为空」或「栈为空」

• 通过循环实现遍历

  1. curr 存在时，将 curr 压入栈，将 curr 的值压入队列头部，并令 curr 指向其右孩子节点

  2. 如果 curr 为空，弹出栈顶元素，将 curr 指向被弹出栈顶节点的左孩子节点

模版代码

public class PostorderTraversal {
    public List<Integer> postorderTraversal(TreeNode root) {
        // 注意这里要指定为LinkedList(双向队列)，不然无法使用addFirst()方法
        LinkedList<Integer> result = new LinkedList<>();
        Stack<TreeNode> tempStack = new Stack<>();
        TreeNode curr = root;

        while (null != curr || !tempStack.empty()) {
            if (null != curr) {
                tempStack.push(curr);
                // 这里需要使用addFirst()将元素压入队列头部
                result.addFirst(curr.val);
                curr = curr.right;
            }
            if (null == curr) {
                curr = tempStack.pop().left;
            }
        }

        return result;
    }
}

---

参考文章：

动画理解二叉树遍历

非递归实现二叉树前序遍历

非递归实现二叉树中序遍历