[正睿集训2021] 字符串

[JSOI2019] 节日庆典

题目描述

点此看题

解法

考虑维护一个备选答案集合 (p)，然后我们挨个处理前缀，假设现在处理到了前缀 (k)，那么任意两个 (p) 中的元素 (i<j)，满足 (lcp(s[i:],s[j:])>j-k)，如果 (k) 向右移了一格，那么 (p) 里面会增加元素 (k)

考虑现在有哪些元素会被清除出 (p)，暴力枚举每对 ((i,j)) 复杂度太高，我们把所有串按长度排序，那么对于串 (i) 首先考虑他能不能弹出最长的串，如果不能弹出那么他也不能弹出更短的串，所以只要枚举 (i) 就行了，时间复杂度 (O(sum|P|))

现在考虑怎么算答案，我们从备选答案集合里选一个最好的就行了，问题变成了比较两个元素谁更好，请看下图：

绿色的段已经不用比了，然后考虑比蓝色段的字典序大小。比字典序大小通常先找 ( t lcp)，发现可以使用 ( t exkmp)，求原串的某个后缀和原串的最长公共前缀其实就是 (Z) 函数，那么比较就可以做到 (O(1))，这部分时间复杂度 (O(sum |P|))

但是如果 (P) 中元素很多复杂度直接上天，现在我们要证明 (P) 中的元素不会很多，引用巨佬的证明：

设两个元素 (i,j) 满足 (2|j|>|i|>|j|)，那么一定有形如 (AAB,AB,B) 这样三个串，如果 (B<A) 那么 (B) 是最优解，如果 (A<B) 并且比完了（比如bb和bba）那么 (B) 是最优解，如果没有比完那么 (AAB) 是最优解。所以每次串长都会扩大 (2) 倍，(p) 中的元素个数只有 (O(log)) 个，总时间复杂度 (O(nlog n))

热身题

题目描述

对于长度 (n) 的字符串 (S)，定义：

[f(i,j)=max{k|0leq kleq j-i,S[i,i+k-1]=S[j-k+1,j]} ]

对于 (0/1) 字符串 (S)，求 (sum_{1<i<jleq n}f(i,j))

(nleq 1e6)，保证 (S) 使用线性同余随机生成。

解法

观察 (k) 可能产生贡献的条件，其实就是子串的一个 ( t border)，但是一个子串的 ( t border) 有很多，只有最大的一个 ( t border) 才会真正算进答案。

这种类型的问题我们通常采取 算贡献 的方法解决，但是我们怎么知道哪个是最大的 ( t border)？是的，我们不能知道，但是我们只要 改变贡献的权值 ，这样让全部加起来即便不需要知道也能算对。

相信你还是有点云里雾里，由于一个串的次大 ( t border) 等于它 ( t border) 的 ( t border)，那么我们令 (w(T)=|T|-|border_T|)，把子串的所有 ( t border) 权值加起来就可以得到正确答案。

还有一点，因为 保证S使用线性同余随机生成，所以长度为 (L) 的 ( t border) 出现概率是 (frac{n^2}{2^L})，那么我们就可以不考虑 (L>5log n) 的 ( t border)，这样先枚举一个位置 (i)，枚举它的长度，用后缀自动机找到他的所有出现位置，( t border) 就用 ( t kmp) 暴力跑，然后从这些出现位置中选两个就可以产生贡献，乘上组合数 ({cntchoose 2}) 即可。

时间复杂度 (O(nlog n))

[HDU 6405] Make ZYB Happy

题目描述

给出 (n) 个字符串 (S_1-S_n)，每个字符串有收益 (w_i)，对于一个字符串 (T)，定义其价值为 (prod_{Tin S_i}w_i)，就表示如果 (T) 是 (S_i) 的子串才能有贡献。

多次询问，每次给出一个 (m)，求出所有长度不超过 (m) 的小写字符串价值的期望。

(nleq 10000,sum|S_i|leq 3e5,qle3e5,mleq 1e6)

解法

第一，这道题并不是毒瘤题。第二，我是傻逼。

不会真的有人去枚举所有不超过 (T) 的小写字符串吧？其实枚举每一个 (S) 的子串就行了。

既然是枚举子串可以考虑用后缀自动机优化，直接建出这 (n) 个串的广义后缀自动机，在构建广义 (Sam) 的时候打一下差分标记，然后 ( t dfs) 一遍就可以统计出每个节点的贡献。每个节点的长度又是连续的，所以直接线段树就行了。

例1

题目描述

有两个字符串 (S,T) 均只由 (R,B) 两种字符组成。有两个非空字符串 (P,Q) 均由 (0,1) 组成，并将 (S,T) 中的 (R,B) 分别替换为 (P,Q)，如果两者替换后的结果相同则称为是合法的。

将不同的 (P,Q)（长度(leq n)）并且能够使 (S,T) 合法的数量记为 (f(S,T))，现在给出由 (R,B,?) 三种字符构成的 (S',T')，如果将问号随机替换成 (R/B)，得到 (f(S,T)) 的期望。

(n,|S|,|T|leq 300000)

解法

首先考虑如果没有问号应该怎么做？

如果 (S,T) 最前面都是 (R) 或者都是 (B) 那么可以直接删掉，那么现在的第一个位置一定有一个是 (R) 一个是 (B)，画图永远是字符串题的第一生产力，设 (R) 对应的长度要小一些：

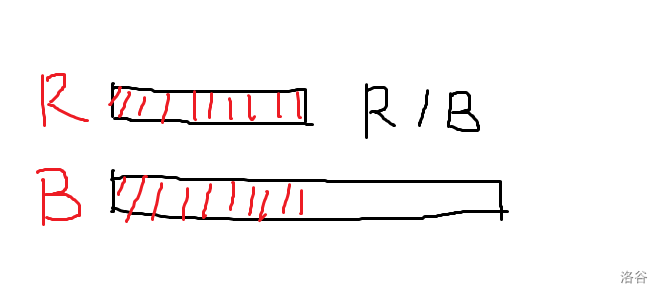
那么无论第一个串后面接的 (R/B)，红色部分总是会循环出现的（因为已经有第一个 (R) 给它打基础了），所以得到一个重要的结论：P是Q的一个周期 ；还因为结尾也一定是一个 (R) 一个 (B) 的，所以 (P) 既在 (Q) 的前面又在 (Q) 的后面，所以有了另一个重要的结论：P是Q的border

综合上面两个结论，我们想推出来一些更有趣的东西。我们可以知道 (|Q|-|P|) 是 (Q) 的一个 ( t border)，那么根据弱周期引理，(gcd(|P|,|Q|-|P|)=gcd(|P|,|Q|)) 也是 (Q) 的一个周期，那么对于一个串 (L)，(P=L^p,Q=L^q)（也就是 (L) 重复若干次），并且 (p,q) 互质。

那么两个串相不相同就和是什么没有关系了，而只和循环节的个数有关，不妨设 (S_R) 为 (S) 中 (R) 的数量，(S_B,T_R,T_B) 同理，则：

[ans=sum_{L=1}^nsum_{p=1}^{n/L}sum_{q=1}^{n/L}[(p,q)=1][pS_R+qS_B=pT_R+qT_B] imes 2^L ]

里面的那个判断柿可以化简一下，设 (Delta R=S_R-T_R,Delta B=T_B-S_B)，那么可以写成这样：

[pDelta R=qDelta B ]

第一种情况是 (Delta R=Delta B=0)，此种情况下只需要满足 (p,q) 互质：

[ans=sum_{L=1}^n2^L(2sum_{j=1}^{n/L}varphi(j)-1) ]

上面的直接 (O(sqrt n)) 整除分块做了。

否则因为 (p,q) 互质，不难推出 (Delta R) 是 (q) 的倍数，(Delta B) 是 (p) 的倍数，设 (k=frac{Delta B}{p}=frac{Delta R}{q})，那么 (Delta B=kp,Delta R=kq)，所以 (gcd(Delta B,Delta R)=k)，把介个东西代换回去：(p=frac{Delta B}{gcd(Delta B,Delta R)},q=frac{Delta R}{gcd(Delta B,Delta R)})，所以 p,q是唯一确定的

那么只需要 (L) 能够使这样的 (p,q) 被枚举到就可以用贡献，那么答案是这样的：

[ans=sum_{L=1}^{frac{n}{max(p,q)}}2^L ]

然后答案可以 (O(1)) 算啦！

---

回到真正的本题，因为有问号的存在，所以我们枚举 (?) 的取值对 (Delta B) 和 (Delta R) 的影响就行了，枚举 (Delta R) 的增量为 (d)：

[sum_{i=-T_?}^{S_?}F(Delta R+d,Delta B-S_?+T_?+d)sum_{i=max(0,d)}^{min(S_?,T_?+d)}{S_?choose i}{T_?choose i-d} ]

后面那个东西是一个组合恒等式，可以用组合意义来说明：

[sum{S_?choose S_?-i}{T_?choose i-d}={S_?+T_?choose S_?-d} ]

由于第一种情况最多出现一次，那么总复杂度 (O(n))