[国集论文笔记] 浅谈保序回归问题

1.前言

这个东西其实就是把国家集训队的论文照抄下来，但是由于作者会加一些自己的理解（相当于是加注释），希望能让原本晦涩的论文好懂一些，也方便自己复习。

由于我看得比较慢，所以这篇文章可能更新得很慢

2.保序回归问题

偏序关系

设 (R) 是集合 (S) 上的一个二元关系，若 (R) 满足：

• 自反性：(forall xin S)，有 (xspace Rspace x)
• 反对称性：(forall x,yin S)，若有 (xspace Rspace y,yspace Rspace x)，则有 (x=y)
• 传递性：(forall x,y,zin S)，若有 (xspace Rspace y,yspace Rspace z)，则有 (xspace Rspace z)

那么就称为 (R) 为 (S) 上的非严格偏序关系，记作 (preceq)

这个东西感性理解一下就行，(oier) 谁管这些定义？

问题描述

我们有一张 (n) 个点的表示偏序关系的有向图，给定两个代价数组 (y) 和 (w)，每条边表示连接的两个点之间有直接的偏序关系，那么图上两个点满足 (v_ipreceq v_j) 当且仅当在图上有一条简单路径。

求数组 (f) 满足 (forall v_ipreceq v_j)，都有 (f_ileq f_j)，那么最小化回归代价：

[sum_{i=1}^nw_i|f_i-y_i|^p,1leq p<infty ]

[max_{i=1}^nw_i|f_i-y_i|,p=infty ]

对于 (p) 相同的保序回归，我们称之为 (L_p) 问题。

所以为什么要叫保序回归问题？因为他能在保证顺序（偏序关系）的情况下最小化回归代价

一些约定

将序列 (z) 中不超过 (a) 的元素变为 (a)，不小于 (b) 的元素变为 (b) 称为序列 (z) 向集合 (S={a,b}) 取整

点集 (U) 的 (L_p) 均值为满足 (sum_{v_iin U}w_i|y_i-k|^p(1leq p<infty)) 或者 (max_{v_iin U}w_i|y_i-k|) 最小的 (k)

也就是如果一堆点非要选一个相同的 (f) 那么选哪个数会最好。

3.特殊情形下的算法

一种贪心算法

例一：题目描述

给定正整数序列 (y,w)，求单调不减的实数序列 (f)，最小化 (sum_{i=1}^nw_i(f_i-y_i)^2)

(nleq 200000)

例一：解法

本题的偏序关系就是 (f_ileq f_j) 的一条链，先给出两个比较重要的结论。

结论1：点集 (U) 的 (L_2) 均值为其加权平均数 (frac{sum_{v_iin U}w_iy_i}{sum_{v_iin U}w_i})

直接把平方展开之后就是二次函数的最值点。

如果有凸单调性但是更为复杂的函数最值，说不定可以让导数为 (0) 然后反解出那个位置的 (x)

结论2：(forall 1leq i<n)，如果有 (y_i>y_{i+1})，那么最优解一定有 (f_i=f_{i+1})

证明用到了微调法和反证法，如果在最优解中 (f_i<f_{i+1})，那么我们选择极小的 (epsilon>0)，得到的 (f_i'=f_i+epsilon w_{i+1},f_{i+1}'=f_{i+1}-epsilon w_i)，你可能觉得这样微调有点奇怪，但是这样能让微调的变化取决于 (y_i) 和 (y_{i+1}) 的关系，展开就知道了：

[w_i(f_i'-y_i)^2+w_{i+1}(f_{i+1}'-y_{i+1})^2-w_i(f_i-y_i)^2-w_{i+1}(f_{i+1}-y_{i+1})^2 ]

[=-2epsilon w_{i}w_{i+1}(f_{i+1}-f_i+y_i-y_{i+1})+epsilon^2w_iw_{i+1}(w_i+w_{i+1})<0 ]

虽然我不是很懂极限，这个柿子和 (0) 的关系取决于一阶无穷小的大小，那么微调后答案变小，所以矛盾。

回到这道题，我们考虑怎么利用这两个结论，由于 (f) 取等的条件是 (y_i>y_{i+1})，那么我们可以维护关于 (y) 的单调不减的单调栈，如果已知一个集合中的点取的 (f) 是相同的，那么可以把这个集合合并为一个点考虑，最优取值就是其 (L_2) 均值，具体的算法流程是这样的：

• 维护一个单调栈，栈内的每个元素为 ((S_i,y_i',w_i'))，分别表示这个元素代表的集合，这个集合的 (L_2) 均值，这个集合的 (w_i) 的求和。
• 每次就加入 (({i},y_i,w_i))，如果有 (y'_{top}>y_i)，那么直接把这两个集合合并，新集合的 (L_2) 均值也可以很好地算出来，那么把原来的元素删除，再把 (({i}|S_{top},frac{y_i+y'_{top}}{w_i+w'_{top}},w_i+w'_{top})) 加入单调栈中即可，然后继续看这个元素能不能弹出栈顶。
• 最后 (f_i) 就是集合包含 (i) 元素的 (L_2) 均值（也就是 (y'_{x})）

上述算法的时间复杂度 (O(nlog n))（因为好像要维护集合），如果能算出 (L_p) 均值那么是可以向 (L_p(1leq p<infty)) 扩展的。

这个算法的局限性在于结论 (2) 并不是一直适用的，如果换了一个偏序关系就 (gg) 了。

维护折线算法

他说这个方法在 (dp) 优化里面挺常用的，但是我怎么没听说过啊喂

例二：题目描述

给定一个 (n) 个点 (n-1) 条边的有向弱连通图，每个点有点权 (d_i) 和修改耗时 (w_i)，对于每个 (i(1leq ileq n))，每次修改可以花费 (w_i) 的时间把 (d_i) 加 (1) 或者减 (1)，求最少消耗多少时间使得每一条边 ((u,v)) 的都满足 (d_uleq d_v)

(nleq 3 imes10^5,1leq d_ileq 1e9,1leq w_ileq 10^4)

弱连通图就是把有向边换成无向边之后原图联通，换句话说就是保证了原图的树形结构。

例二：解法

首先由于偏序关系是非严格的，所以最后每个点的权值一定是某一个原来的 (d)

考虑用树形 (dp) 解决问题，设 (g(u,i)) 表示把点 (u) 变成 (d_i) 并且解决 (u) 子树的最小花费，不难发现取决于边的方向可以从 (g(v,1...i)) 或者 (g(v,i...n)) 转移而来，所以维护前缀最小值 (L_i) 和后缀最小值 (R_i) 就可以做到 (O(n^2)) 了。

更好的做法需要结论，维护折线优化 (dp) 首先需要找图像的性质，先考虑叶子节点，把 (g,L,R) 三个数组放在平面直角坐标上，发现斜率单调不减，因为图画出来是这样的（我知道你们都懒得画）：

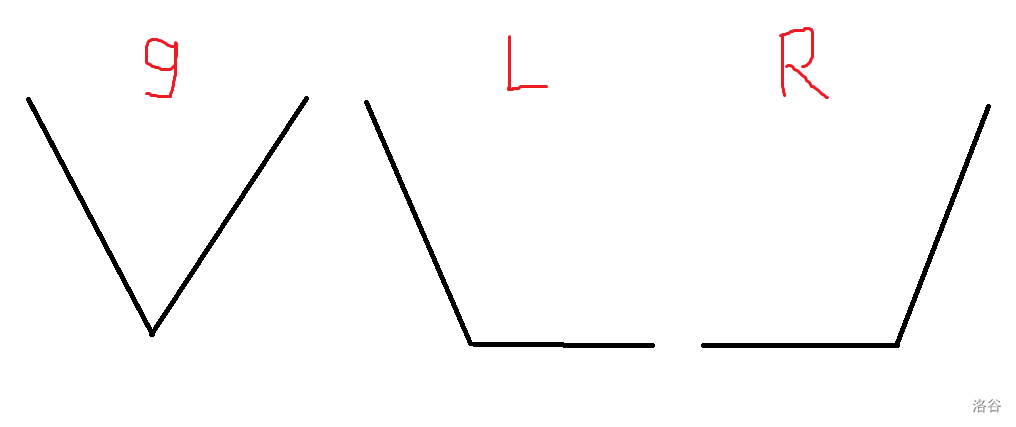
对于非叶节点，(g_u) 是若干个斜率单调不减函数的叠加（对应位置函数值相加），所以 (g_u) 也是一个斜率单调不减的函数。(L_u) 和 (R_u) 就是 (g_u) 把一个后缀(/)前缀变成 (0)，所以也是斜率单调不减得函数，那么归纳地证明所有函数都斜率单调不减。

现在问题在于维护这个折线函数，对于叶节点的函数就是区间修改。那么怎么维护叠加操作呢？直接线段树合并就行了。这个线段树虽然带了懒标记，但是合并的时候直接把懒标记加起来是没问题的。

由于 (L,R) 只有其中之一会对祖先产生贡献，所以 (L,R) 的计算可以直接在 (g) 的线段树上二分并修改。时间复杂度 (O(nlog n))

但是最后一步算 (L,R) 我好像不是特别懂诶，可能还要想一下。

UPD：好像并不是很难做，二分找到最低点之后就直接区间修改即可（打标记嘛）