[提高组集训2021] Round1

矩阵删除

题目描述

给一个 (n imes m)的 (01) 矩阵，我们想在每一行删除一个元素，得到一个 (n imes(m-1)) 的矩阵。其中删除的元素的位置 ((i,a_i))，满足 (|a_i-a_{i+1}|leq k)

请问最后能得到多少种本质不同的矩阵，输出答案对 (1e9+7) 取模的值。

解法

考虑 (dp) 解决这个问题，设 (f_{i,j}) 表示第 (i) 行删除第 (j) 个位置仅考虑前 (i) 行得到本质不同的矩阵，转移可以根据题意直接写出，但是很显然本题会算重：

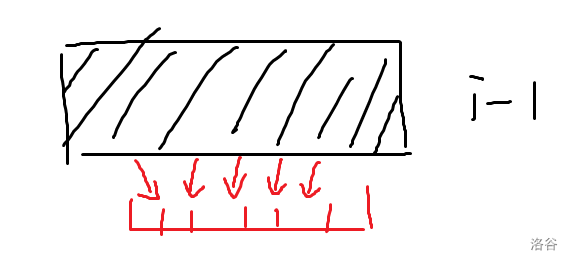
如上图，对前 (i-1) 行的某种情况，可能转移到一个连续相同段，我们需要考虑段内的去重，因为删段内得到的 (i) 这一行是本质相同的。并且我们不需要考虑不同段内的去重，因为它们得到的 (i) 行是一定不同的。

那么段内如何去重呢？考虑一个极长连续相同段 ([l,r])，设 (kin[l,r])，那么我们只需要考虑 (k) 和 (k+1) 两者的重复，因为它们得到前 (i-1) 行的状态相似性是最高的（类比 ( t sa) 求本质不同子串的去重方式），所以其实把不考虑去重算出来的情况减去所有 (k) 和 (k+1) 具有的重复就行了。

可以定义辅助数组 (g_{i,j}) 表示第 (i) 行删除第 (j-1) 个位置和删除第 (j) 个位置得到矩阵本质相同的方案数，两个状态交替转移即可，(j-1) 和 (j) 的重复段是 ([j-k,j+k-1])：

[g_{i,j}=sum_{l=j-k}^{j+k-1} f_{i-1,l}-sum_{l=j-k+1}^{j+k-1} g_{i-1,l} ]

[f_{i,j}=sum_{l=j-k}^{j+k} f_{i-1,l}-sum_{l=j-k+1}^{j+k} g_{i-1,l} ]

简单前缀和优化即可，时间复杂度 (O(nm))

总结

相似去重法一定要积累下来，找两个最相似的元素去重即可。

#include <cstdio>
#include <iostream>
using namespace std;
const int M = 3005;
const int MOD = 1e9+7;
int read()
{
	int x=0,f=1;char c;
	while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
	while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
	return x*f;
}
int n,m,k,w[M][M],f[M][M],g[M][M];
int main()
{
	freopen("matrix.in","r",stdin);
	freopen("matrix.out","w",stdout);
	n=read();m=read();k=read();
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			scanf("%1d",&w[i][j]);
	for(int i=1;i<=m;i++)
	{
		f[1][i]=1+f[1][i-1];
		g[1][i]=(i>1 && w[1][i]==w[1][i-1])+g[1][i-1];
	}
	for(int i=2;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		{
			int a=min(j+k,m),b=max(j-k-1,0);
			int c=min(j+k-1,m),d=max(j-k,0);
			f[i][j]=f[i-1][a]-f[i-1][b]
			-g[i-1][a]+g[i-1][d];
			if(j>1 && w[i][j]==w[i][j-1])
				g[i][j]=f[i-1][c]-f[i-1][b]
				-g[i-1][c]+g[i-1][d];
		}
		for(int j=1;j<=m;j++)
		{
			f[i][j]=(f[i][j]%MOD+MOD)%MOD;
			g[i][j]=(g[i][j]%MOD+MOD)%MOD;
			f[i][j]=(f[i][j]+f[i][j-1])%MOD;
			g[i][j]=(g[i][j]+g[i][j-1])%MOD;
		}
	}
	printf("%d
",(f[n][m]-g[n][m]+MOD)%MOD);
}

路径查询

题目描述

给你一个 (n) 个点 (m) 条边的无向图，边有边权，你需要回答 (q) 次询问，每次给定两个点 (u,v)，试求出所有路径中第二大的边权的最小值是多少。

(1leq n,qleq 10^5,1leq mleq 2 imes 10^5,1leq wleq 10^9)

解法

有一个简单的问题转化，我们从大到小加入边 (e)，如果此时某个询问 ((u,v)) 只差一条没有加入的边就能够联通，那么询问 ((u,v)) 的答案就是 (e) 的边权。

自然想到维护每个连通块通过未加入的边能够到达的块外的点集 (S)，那么询问如何处理呢？一个很神奇的想法是把询问也放在连通块上，维护每个连通块和块外之间的询问集合 (Q)，关键问题是合并。

要保证复杂度肯定首选启发式合并，这里我们按照 (S) 和 (Q) 的大小之和来启发式合并，设要把 (x) 合并到 (y) 上，那么考虑 (S_x) 能不能回答 (Q_y)，(Q_x) 能不能被 (S_y) 回答，那么我们只需要遍历小的那一边即可。

每个点还是只会被合并 (log n) 次，因为我们还要用 ( t set) 等大常数数据结构，所以时间复杂度 (O(nlog ^2n))

总结

把询问和修改过程一起考虑，那么就能在变化时立即考虑到会被影响的询问。

#include <cstdio>
#include <vector>
#include <iostream>
#include <algorithm>
#include <set>
using namespace std;
const int M = 400005;
#define pii pair<int,int>
#define mp make_pair
int read()
{
	int x=0,f=1;char c;
	while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
	while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
	return x*f;
}
int n,m,k,fa[M],ans[M];set<int> e[M];set<pii> q[M];
struct node
{
	int u,v,c;
	bool operator < (const node &b) const
	{
		return c<b.c;
	}
}b[M<<1];
int find(int x)
{
	if(x!=fa[x]) fa[x]=find(fa[x]);
	return fa[x];
}
void merge(int x,int y,int val)
{
	if(x==y) return;//no need to merge
	fa[x]=y;
	//edge of X contribute to the query of Y
	for(auto u:e[x]) while(1)//multiple querys
	{
		set<pii>::iterator it=
		q[y].lower_bound(mp(u,0));
		if(it==q[y].end() || it->first!=u)
			break;//not the query
		ans[it->second]=val;
		q[y].erase(it);
		q[u].erase(mp(y,it->second));
	}
	//query of X asking the edge of Y
	vector<pii> rnm;
	for(auto u:q[x]) if(e[y].count(u.first))
	{
		ans[u.second]=val;
		q[u.first].erase(mp(x,u.second));
		rnm.push_back(u);
	}
	for(auto u:rnm) q[x].erase(u);
	//add the edge of X to edge of Y
	for(auto u:e[x])
	{
		e[u].erase(x);
		if(u!=y)
		{
			e[u].insert(y);
			e[y].insert(u);
		}
	}
	//add the query of X to the query of Y
	for(auto u:q[x])
	{
		q[u.first].erase(mp(x,u.second));
		q[u.first].insert(mp(y,u.second));
		q[y].insert(u);
	}
	q[x].clear();e[x].clear();
}
int main()
{
	freopen("path.in","r",stdin);
	freopen("path.out","w",stdout);
	n=read();m=read();k=read();
	for(int i=1;i<=n;i++) fa[i]=i;
	for(int i=1;i<=m;i++)
	{
		int u=read(),v=read(),c=read();
		e[u].insert(v);
		e[v].insert(u);
		b[i]=node{u,v,c};
	}
	for(int i=1;i<=k;i++)
	{
		int u=read(),v=read();
		if(e[u].count(v))
		{
			ans[i]=-2333;
			continue;
		}
		q[u].insert(mp(v,i));
		q[v].insert(mp(u,i));
	}
	sort(b+1,b+1+m);
	for(int i=1;i<=m;i++)
	{
		int u=find(b[i].u),v=find(b[i].v);
		if(e[u].size()+q[u].size()>
		e[v].size()+q[v].size()) swap(u,v);
		merge(u,v,b[i].c);
	}
	for(int i=1;i<=k;i++)
	{
		if(ans[i]==-2333) puts("0");
		else if(ans[i]==0) puts("-1");
		else printf("%d
",ans[i]);
	}
}