- 黄色和灰色是问题,粉色是重点。
- Deep Learning强大的地方就是可以利用网络中间某一层的输出当做是数据的另一种表达,从而可以将其认为是经过网络学习到的特征。基于该特征,可以进行进一步的相似度比较等。
- 现在,CNN已经成为众多科学领域的研究热点之一,特别是在模式分类领域,由于该网络避免了对图像的复杂前期预处理,可以直接输入原始图像,因而得到了更为广泛的应用。
一般地,CNN的基本结构包括两层,其一为特征提取层,每个神经元的输入与前一层的局部接受域相连,并提取该局部的特征。一旦该局部特征被提取后,它与其它特征间的位置关系也随之确定下来;其二是特征映射层,网络的每个计算层由多个特征映射组成,每个特征映射是一个平面,平面上所有神经元的权值相等。特征映射结构采用影响函数核小的sigmoid函数作为卷积网络的激活函数,使得特征映射具有位移不变性。此外,由于一个映射面上的神经元共享权值,因而减少了网络自由参数的个数。卷积神经网络中的每一个卷积层都紧跟着一个用来求局部平均与二次提取的计算层,这种特有的两次特征提取结构减小了特征分辨率。
CNN主要用来识别位移、缩放及其他形式扭曲不变性的二维图形。由于CNN的特征检测层通过训练数据进行学习,所以在使用CNN时,避免了显示的特征抽取,而隐式地从训练数据中进行学习;再者由于同一特征映射面上的神经元权值相同,所以网络可以并行学习,这也是卷积网络相对于神经元彼此相连网络的一大优势。卷积神经网络以其局部权值共享的特殊结构在语音识别和图像处理方面有着独特的优越性,其布局更接近于实际的生物神经网络,权值共享降低了网络的复杂性,特别是多维输入向量的图像可以直接输入网络这一特点避免了特征提取和分类过程中数据重建的复杂度。
1. 神经网络
首先介绍神经网络,这一步的详细可以参考资源1。简要介绍下。神经网络的每个单元如下:
其对应的公式如下:
其中,该单元也可以被称作是Logistic回归模型。当将多个单元组合起来并具有分层结构时,就形成了神经网络模型。下图展示了一个具有一个隐含层的神经网络。
其对应的公式如下:
比较类似的,可以拓展到有2,3,4,5,…个隐含层。
神经网络的训练方法也同Logistic类似,不过由于其多层性,还需要利用链式求导法则对隐含层的节点进行求导,即梯度下降+链式求导法则,专业名称为反向传播。关于训练算法,本文暂不涉及。
2 卷积神经网络
在图像处理中,往往把图像表示为像素的向量,比如一个1000×1000的图像,可以表示为一个1000000的向量。在上一节中提到的神经网络中,如果隐含层数目与输入层一样,即也是1000000时,那么输入层到隐含层的参数数据为1000000×1000000=10^12,这样就太多了,基本没法训练。所以图像处理要想练成神经网络大法,必先减少参数加快速度。
2.1 局部感知
卷积神经网络有两种神器可以降低参数数目,第一种神器叫做局部感知野。
如下图所示:左图为全连接,右图为局部连接。

在上右图中,假如每个神经元只和10×10个像素值相连,那么权值数据为1000000×100个参数,减少为原来的千分之一。而那10×10个像素值对应的10×10个参数,其实就相当于卷积操作。
2.2 参数共享
但其实这样的话参数仍然过多,那么就启动第二级神器,即权值共享。在上面的局部连接中,每个神经元都对应100个参数,一共1000000个神经元,如果这1000000个神经元的100个参数都是相等的,那么参数数目就变为100了。
怎么理解权值共享呢?我们可以这100个参数(也就是卷积操作)看成是提取特征的方式,该方式与位置无关。这其中隐含的原理则是:图像的一部分的统计特性与其他部分是一样的。这也意味着我们在这一部分学习的特征也能用在另一部分上,所以对于这个图像上的所有位置,我们都能使用同样的学习特征。
更直观一些,当从一个大尺寸图像中随机选取一小块,比如说 8×8 作为样本,并且从这个小块样本中学习到了一些特征,这时我们可以把从这个 8×8 样本中学习到的特征作为探测器,应用到这个图像的任意地方中去。特别是,我们可以用从 8×8 样本中所学习到的特征跟原本的大尺寸图像作卷积,从而对这个大尺寸图像上的任一位置获得一个不同特征的激活值。
如下图所示,展示了一个33的卷积核在55的图像上做卷积的过程。每个卷积都是一种特征提取方式,就像一个筛子,将图像中符合条件(激活值越大越符合条件)的部分筛选出来。

2.3 多卷积核
上面所述只有100个参数时,表明只有1个100*100的卷积核,显然,特征提取是不充分的,我们可以添加多个卷积核,比如32个卷积核,可以学习32种特征。在有多个卷积核时,如下图所示:

上图右,不同颜色表明不同的卷积核。每个卷积核都会将图像生成为另一幅图像。比如两个卷积核就可以将生成两幅图像,这两幅图像可以看做是一张图像的不同的通道。
下图展示了在四个通道上的卷积操作,有两个卷积核,生成两个通道。其中需要注意的是,四个通道上每个通道对应一个卷积核,先将w2忽略,只看w1,那么在w1的某位置(i,j)处的值,是由四个通道上(i,j)处的卷积结果相加然后再取激活函数值得到的。


所以,在上图由4个通道卷积得到2个通道的过程中,参数的数目为4×2×2×2个,其中4表示4个通道,第一个2表示生成2个通道,最后的2×2表示卷积核大小。
2.4 Down-pooling
在通过卷积获得了特征 (features) 之后,下一步我们希望利用这些特征去做分类。理论上讲,人们可以用所有提取得到的特征去训练分类器,例如 softmax 分类器,但这样做面临计算量的挑战。例如:对于一个 96X96 像素的图像,假设我们已经学习得到了400个定义在8X8输入上的特征,每一个特征和图像卷积都会得到一个 (96 − 8 + 1) × (96 − 8 + 1) = 7921 维的卷积特征,由于有 400 个特征,所以每个样例 (example) 都会得到一个 892 × 400 = 3,168,400 维的卷积特征向量。学习一个拥有超过 3 百万特征输入的分类器十分不便,并且容易出现过拟合 (over-fitting)。
为了解决这个问题,首先回忆一下,我们之所以决定使用卷积后的特征是因为图像具有一种“静态性”的属性,这也就意味着在一个图像区域有用的特征极有可能在另一个区域同样适用。因此,为了描述大的图像,一个很自然的想法就是对不同位置的特征进行聚合统计,例如,人们可以计算图像一个区域上的某个特定特征的平均值 (或最大值)。这些概要统计特征不仅具有低得多的维度 (相比使用所有提取得到的特征),同时还会改善结果(不容易过拟合)。这种聚合的操作就叫做池化 (pooling),有时也称为平均池化或者最大池化 (取决于计算池化的方法)。

至此,卷积神经网络的基本结构和原理已经阐述完毕。
2.5 多层卷积
在实际应用中,往往使用多层卷积,然后再使用全连接层进行训练,多层卷积的目的是一层卷积学到的特征往往是局部的,层数越高,学到的特征就越全局化。
3 ImageNet-2010网络结构
ImageNet LSVRC是一个图片分类的比赛,其训练集包括127W+张图片,验证集有5W张图片,测试集有15W张图片。本文截取2010年Alex Krizhevsky的CNN结构进行说明,该结构在2010年取得冠军,top-5错误率为15.3%。值得一提的是,在今年的ImageNet LSVRC比赛中,取得冠军的GoogNet已经达到了top-5错误率6.67%。可见,深度学习的提升空间还很巨大。
下图即为Alex的CNN结构图。需要注意的是,该模型采用了2-GPU并行结构,即第1、2、4、5卷积层都是将模型参数分为2部分进行训练的。在这里,更进一步,并行结构分为数据并行与模型并行。数据并行是指在不同的GPU上,模型结构相同,但将训练数据进行切分,分别训练得到不同的模型,然后再将模型进行融合。而模型并行则是,将若干层的模型参数进行切分,不同的GPU上使用相同的数据进行训练,得到的结果直接连接作为下一层的输入。
链接:https://www.zhihu.com/question/53851014/answer/158794752
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
首先说下为什么要并行,众所周知目前的深度学习领域就是海量的数据加上大量的数学运算,所以计算量相当的大,训练一个模型跑上十天半个月啥的是常事。那此时分布式的意义就出现了,既然一张GPU卡跑得太慢就来两张,一台机器跑得太慢就用多台机器,于是我们先来说说数据并行,放张网上copy的图
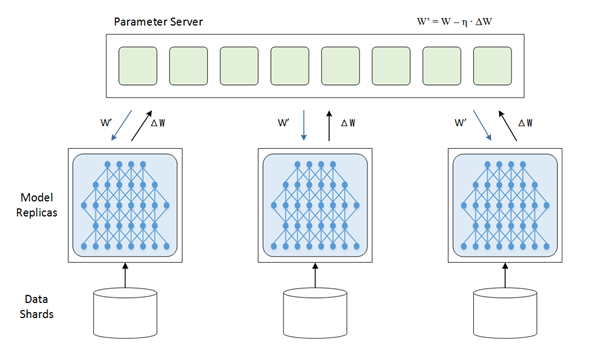
在上面的这张图里,每一个节点(或者叫进程)都有一份模型,然后各个节点取不同的数据,通常是一个batch_size,然后各自完成前向和后向的计算得到梯度,这些进行训练的进程我们成为worker,除了worker,还有参数服务器,简称ps server,这些worker会把各自计算得到的梯度送到ps server,然后由ps server来进行update操作,然后把update后的模型再传回各个节点。因为在这种并行模式中,被划分的是数据,所以这种并行方式叫数据并行。
然后呢咱们来说说模型并行,深度学习的计算其实主要是矩阵运算,而在计算时这些矩阵都是保存在内存里的,如果是用GPU卡计算的话就是放在显存里,可是有的时候矩阵会非常大,比如在CNN中如果num_classes达到千万级别,那一个FC层用到的矩阵就可能会大到显存塞不下。这个时候就不得不把这样的超大矩阵给拆了分别放到不同的卡上去做计算,从网络的角度来说就是把网络结构拆了,其实从计算的过程来说就是把矩阵做了分块处理。这里再放一张网上盗的图表示下模型并行:
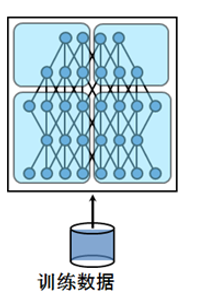
最后说说两者之间的联系,有的时候呢数据并行和模型并行会被同时用上。比如深度的卷积神经网络中卷积层计算量大,但所需参数系数 W 少,而FC层计算量小,所需参数系数 W 多。因此对于卷积层适合使用数据并行,对于全连接层适合使用模型并行。 就像这样:
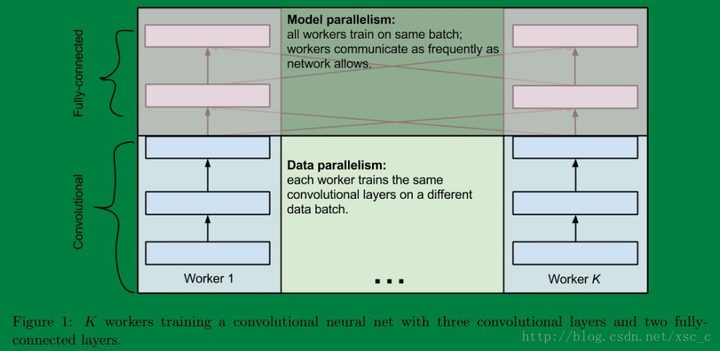
关于这个更多地可以参考这篇博客,说的挺详细的卷积神经网络的并行化模型--One weird trick for parallelizing convolutional neural networks
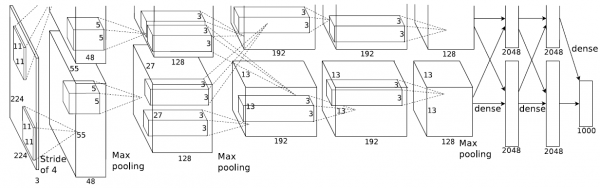
上图模型的基本参数为:
输入:224×224大小的图片,3通道
第一层卷积:5×5大小的卷积核96个,每个GPU上48个。
第一层max-pooling:2×2的核。
对于mean pooling,真的是好简单:假设pooling的窗大小是2x2, 在forward的时候啊,就是在前面卷积完的输出上依次不重合的取2x2的窗平均,得到一个值就是当前mean pooling之后的值。backward的时候,把一个值分成四等分放到前面2x2的格子里面就好了。如下
forward: [1 3; 2 2] -> [2]
backward: [2] -> [0.5 0.5; 0.5 0.5]
max pooling就稍微复杂一点,forward的时候你只需要把2x2窗子里面那个最大的拿走就好了,backward的时候你要把当前的值放到之前那个最大的位置,其他的三个位置都弄成0。如下
forward: [1 3; 2 2] -> 3
backward: [3] -> [0 3; 0 0]
作者:李济深
链接:https://www.zhihu.com/question/23437871/answer/46491291
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
第二层卷积:3×3卷积核256个,每个GPU上128个。
第二层max-pooling:2×2的核。
第三层卷积:与上一层是全连接,3*3的卷积核384个。分到两个GPU上个192个。
第四层卷积:3×3的卷积核384个,两个GPU各192个。该层与上一层连接没有经过pooling层。
第五层卷积:3×3的卷积核256个,两个GPU上个128个。
第五层max-pooling:2×2的核。
第一层全连接:4096维,将第五层max-pooling的输出连接成为一个一维向量,作为该层的输入。
第二层全连接:4096维
Softmax层:输出为1000,输出的每一维都是图片属于该类别的概率。
softmax https://www.zhihu.com/question/23765351 这里有推导没看懂
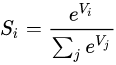
=========================================================================
对于一个32x32x3(宽32像素x高32像素xRGB三通道)的图像,如果我们在CNN的第一个卷积层定义训练12个滤波器,那就这一层的输出便是32X32X12.按照不同的任务,我们可以对这个输出做进一步的处理,这包括激活函数,池化,全连接等。
简单来说,训练CNN在相当意义上是在训练每一个卷积层的滤波器。让这些滤波器组对特定的模式有高的激活,以达到CNN网络的分类/检测等目的。
卷积神经网络的第一个卷积层的滤波器用来检测低阶特征,比如边、角、曲线等。随着卷积层的增加,对应滤波器检测的特征就更加复杂(理性情况下,也是我们想要的情况)。比如第二个卷积层的输入实际上是第一层的输出(滤波器激活图),这一层的滤波器便是用来检测低价特征的组合等情况(半圆、四边形等),如此累积,以检测越来越复杂的特征。
所以,在相当程度上,构建卷积神经网络的任务就在于构建这些滤波器。也就是,将这些滤波器变成这样(改变滤波器矩阵的值,也就是Weight)的——能识别特定的特征。这个过程叫做训练。
在训练开始之时,卷积层的滤波器是完全随机的,它们不会对任何特征激活(不能检测任何特征)。
把一个空白的滤波其,修改其权重(weights)以使它能检测特定的模式,整个过程就如工程里面的反馈。
|
在*有监督学习中,数据是有标注的,以(x, t)的形式出现,其中x是输入数据,t是标注.正确的t标注是ground truth, 错误的标记则不是。(也有人将所有标注数据都叫做ground truth) 由模型函数的数据则是由(x, y)的形式出现的。其中x为之前的输入数据,y为模型预测的值。 标注会和模型预测的结果作比较。在损耗函数(loss function / error function)中会将y 和 t 作比较,从而计算损耗(loss / error)。 比如在最小方差中: |
|
在训练过程就是这样的:第一次训练,输入一张图像,这个图像通过各层卷积处理输出量一组向量[1,1,1,1,1,1,1,1,1,1],也就是,对于完全由随机滤波器构建的网络,其输出认为这张图等概率的是十个类别中的某一种。但是对于训练,我们有一个Gound Thuth, 也就是这张图中物体所属的类别:[0,0,1,0,0,0,0,0,0,0],也就是属于第三类。这时候我们可以定义一个损失函数,比如常见的MSE(mean squared error).我们假定L是这个损失函数的输出。这时候我们的目的就是,让L的值反馈(这种神经网络概念下称为 back propagation,反向传输)给整个卷积神经网络,以修改各个滤波器的权重,使得损失值L最小。
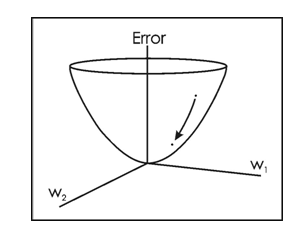
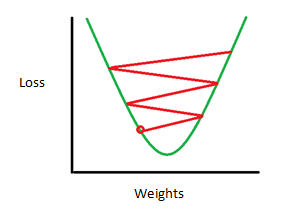
这是一个典型的最优化问题。当然地,在工程上我们几乎不可能一次就把滤波器的权重W修改到使L最小的情况,而是需要多次训练和多次修改。
如果情况理想的话,权重修改的方向是使得L的变化收敛的。这也就是说很可能达到了我们训练这个 神经网络的目的——让各个卷积层的滤波器能够组合起来最优化的检测特定的模式。 -------- |
作者:lee philip
链接:https://www.zhihu.com/question/22464082/answer/21443035
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。