| 这个作业属于哪个班级 | 数据结构--网络2011/2012 |
|---|---|
| 这个作业的地址 | DS博客作业04--图 |
| 这个作业的目标 | 学习图结构设计及相关算法 |
| 姓名 | 唐宇悦 |
0.PTA得分截图

1.本周学习总结
1.1 图的存储结构
1.1.1 邻接矩阵
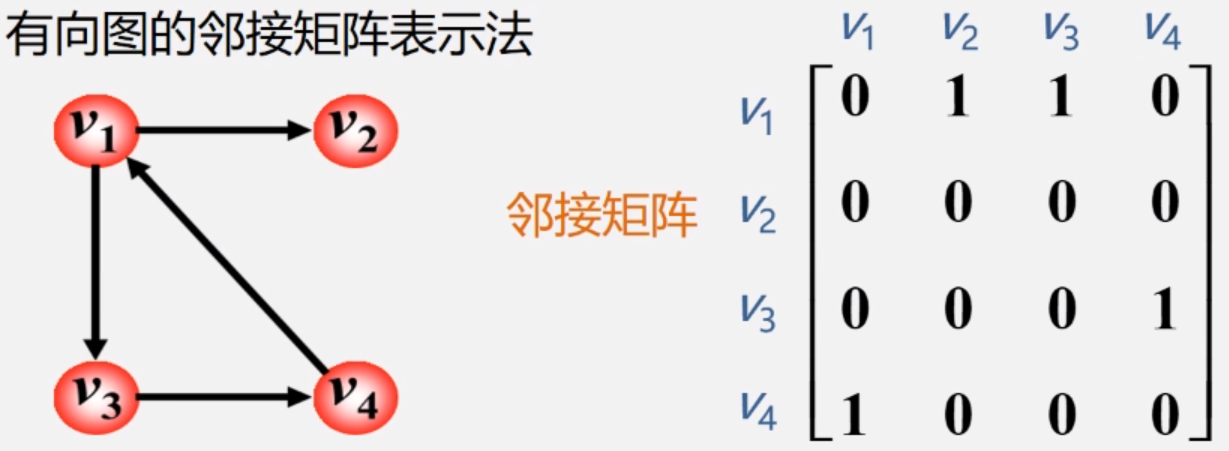
有向图:
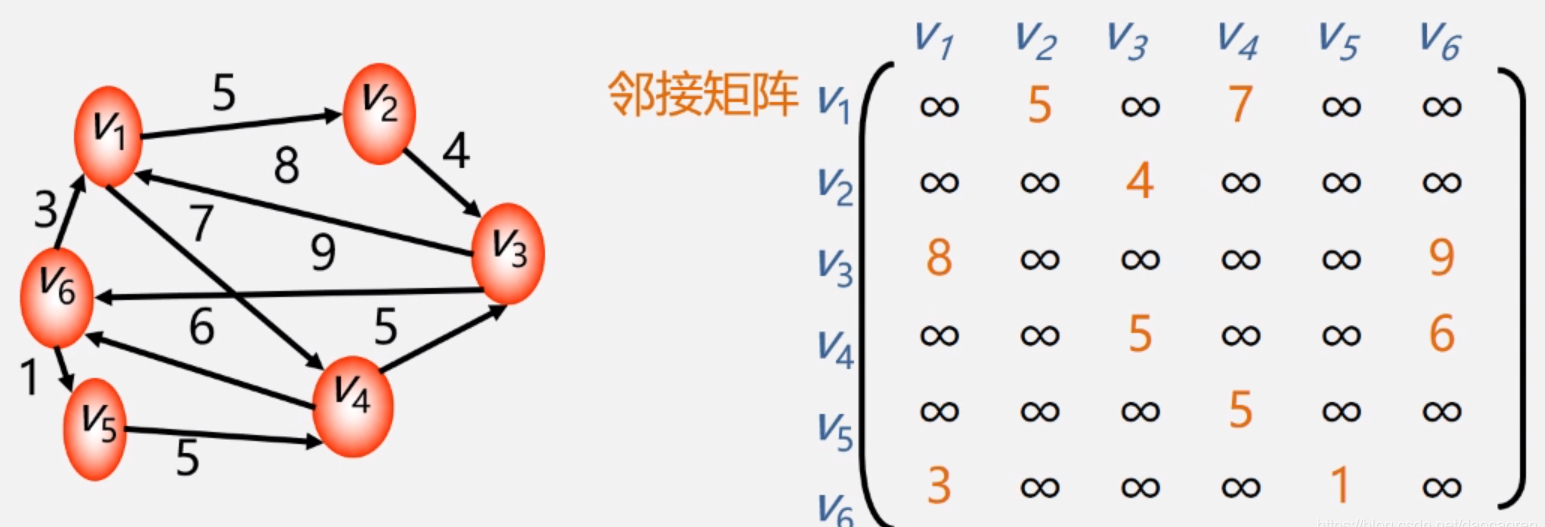
网:
邻接矩阵的结构体定义
#define MaxVertexNum 100; //顶点数目的最大值
typedef char VertexType; //顶点的数据类型
typedef int EdgeType; //带权图中边上权值的数据类型
typedef struct{
VertexType Vex[MaxVertexNum]; //顶点表
EdgeType Edge[MaxVertexNum][MaxVertexNum]; //邻接矩阵,边表
int vexnum, arcnum; //图的当前顶点数和弧树
}MGraph;
建图函数
void CreateMGraph(MGraph &g, int n, int e)//建图
{
//n顶点,e弧数
g.n = n;
g.e = e;
int i, j;
int a, b;//下标
for (i = 1; i <= n; i++)//先进行初始化
{
for (j = 1; j <= n; j++)
{
g.edges[i][j] = 0;
}
}
for (i = 1; i <= e; i++)//无向图
{
cin >> a >> b;
g.edges[a][b] = 1;
g.edges[b][a] = 1;
}
}
图的邻接矩阵存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息,一个二维数组(邻接矩阵)存储图中的边或弧的信息。
设图G有n个顶点,则邻接矩阵是一个n*n的方阵,定义为:
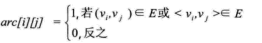
看一个实例,下图左就是一个无向图。

从上面可以看出,无向图的边数组是一个对称矩阵。所谓对称矩阵就是n阶矩阵的元满足aij = aji。即从矩阵的左上角到右下角的主对角线为轴,右上角的元和左下角相对应的元全都是相等的。
从上面可以看出,无向图的边数组是一个对称矩阵。所谓对称矩阵就是n阶矩阵的元满足aij = aji。即从矩阵的左上角到右下角的主对角线为轴,右上角的元和左下角相对应的元全都是相等的。
从这个矩阵中,很容易知道图中的信息。
(1)要判断任意两顶点是否有边无边就很容易了;
(2)要知道某个顶点的度,其实就是这个顶点vi在邻接矩阵中第i行或(第i列)的元素之和;
(3)求顶点vi的所有邻接点就是将矩阵中第i行元素扫描一遍,arc[i][j]为1就是邻接点;
而有向图讲究入度和出度,顶点vi的入度为1,正好是第i列各数之和。顶点vi的出度为2,即第i行的各数之和。
1.1.2 邻接表
邻接表的结构体定义
#define MAXVEX 100; //图中顶点数目的最大值
type char VertexType; //顶点类型应由用户定义
typedef int EdgeType; //边上的权值类型应由用户定义
/*边表结点*/
typedef struct EdgeNode{
int adjvex; //该弧所指向的顶点的下标或者位置
EdgeType weight; //权值,对于非网图可以不需要
struct EdgeNode *next; //指向下一个邻接点
}EdgeNode;
/*顶点表结点*/
typedef struct VertexNode{
Vertex data; //顶点域,存储顶点信息
EdgeNode *firstedge //边表头指针
}VertexNode, AdjList[MAXVEX];
/*邻接表*/
typedef struct{
AdjList adjList;
int numVertexes, numEdges; //图中当前顶点数和边数
}
建图函数
void CreateAdj(AdjGraph *&G, int n, int e)//创建图邻接表
{
int i, j, a, b;
G = new AdjGraph;
for (i = 1; i <= n; i++)//邻接表头结点置零
{
G->adjlist[i].firstarc = NULL;
}
for (j = 1; j <= e; j++)//无向图
{
cin >> a >> b;
ArcNode *p,*q;
p = new ArcNode;
q = new ArcNode;
p->adjvex = b;//用头插法进行插入
q->adjvex = a;
p->nextarc = G->adjlist[a].firstarc;
G->adjlist[a].firstarc = p;
q->nextarc = G->adjlist[b].firstarc;
G->adjlist[b].firstarc = q;
}
G->n = n;
G->e = e;
}
邻接矩阵是不错的一种图存储结构,但是,对于边数相对顶点较少的图,这种结构存在对存储空间的极大浪费。因此,找到一种数组与链表相结合的存储方法称为邻接表。
邻接表的处理方法是这样的:
(1)图中顶点用一个一维数组存储,当然,顶点也可以用单链表来存储,不过,数组可以较容易的读取顶点的信息,更加方便。
(2)图中每个顶点vi的所有邻接点构成一个线性表,由于邻接点的个数不定,所以,用单链表存储,无向图称为顶点vi的边表,有向图则称为顶点vi作为弧尾的出边表。
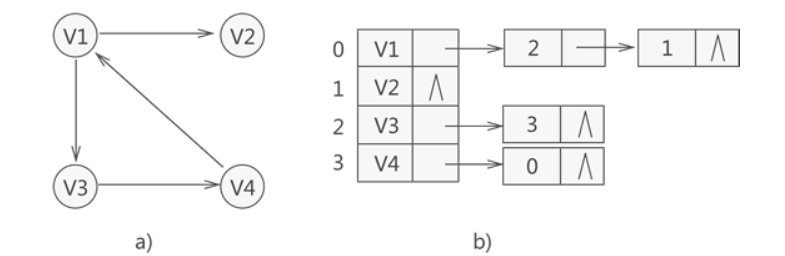
例如,下图就是一个无向图的邻接表的结构。
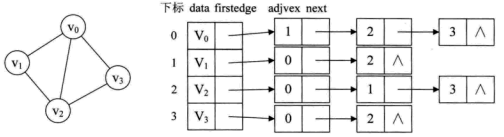
从图中可以看出,顶点表的各个结点由data和firstedge两个域表示,data是数据域,存储顶点的信息,firstedge是指针域,指向边表的第一个结点,即此顶点的第一个邻接点。边表结点由adjvex和next两个域组成。adjvex是邻接点域,存储某顶点的邻接点在顶点表中的下标,next则存储指向边表中下一个结点的指针。
1.1.3 邻接矩阵和邻接表表示图的区别
对于一个具有n个顶点e条边的无向图
它的邻接表表示有n个顶点表结点2e个边表结点
对于一个具有n个顶点e条边的有向图
它的邻接表表示有n个顶点表结点e个边表结点
如果图中边的数目远远小于n2称作稀疏图,这是用邻接表表示比用邻接矩阵表示节省空间;
如果图中边的数目接近于n2,对于无向图接近于n*(n-1)称作稠密图,考虑到邻接表中要附加链域,采用邻接矩阵表示法为宜。
- 时间复杂度
用邻接矩阵构造图时,若存储的是一个无向图,则时间复杂度为O(n^2 + n*e),其中,对邻接矩阵的初始化耗费的时间为O(n^2);
对于DFS,BFS遍历来说,时间复杂度和存储结构有关:
n表示有n个顶点,e表示有e条边。
1.若采用邻接矩阵存储,
时间复杂度为O(n^2);
2.若采用邻接链表存储,建立邻接表或逆邻接表时,
若输入的顶点信息即为顶点的编号,则时间复杂度为O(n+e);
若输入的顶点信息不是顶点的编号,需要通过查找才能得到顶点在图中的位置,则时间复杂度为O(n*e);
1.2 图遍历
1.2.1 深度优先遍历
⑴ 访问顶点v;
⑵ 从v的未被访问的邻接点中选取一个顶点w,从w出发进行深度优先遍历;
⑶ 重复上述两步,直至图中所有和v有路径相通的顶点都被访问到。
首先,我们访问V1结点,V1结点入栈并输出,然后发现V1与V2相连,因此我们将V2入栈,同理,V4和V5也入栈输出,因此遍历序列为V1 V2 V4 V5

接下来,V5入栈输出后,我们发现与V5相连的两个结点都已经访问过了,因此V5直接出栈,返回到了上一层,即V4,在V4结点处我们发现还有一个结点V8没有被访问到,因此将V8入栈并输出
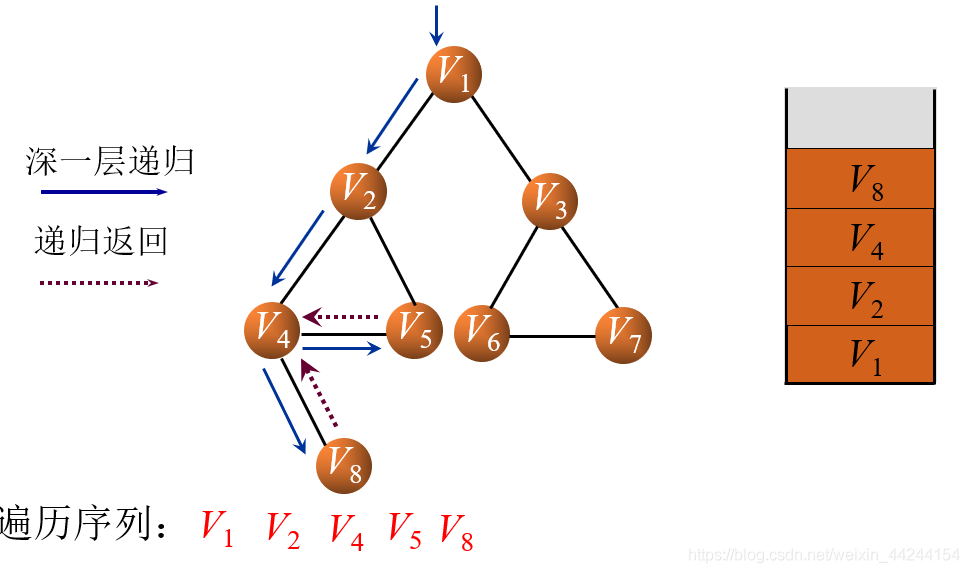
同理,V8入栈后会直接出栈,因为与V8相邻的结点都已经被访问过了,接下来V4、V2也出栈,只留下了V1在堆栈中
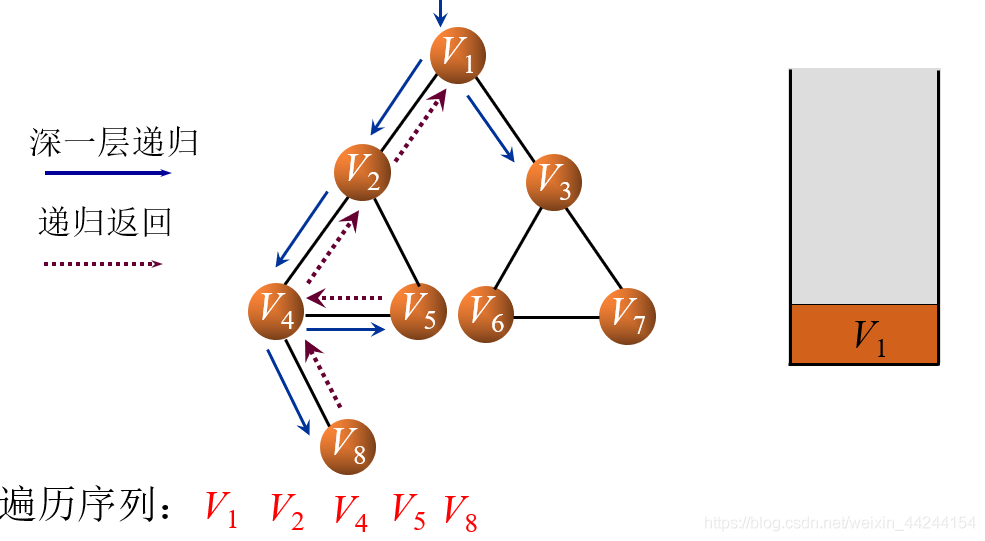
这时我们会发现,V1还有结点没有访问到!所以V3、V6、V7相继入栈并输出
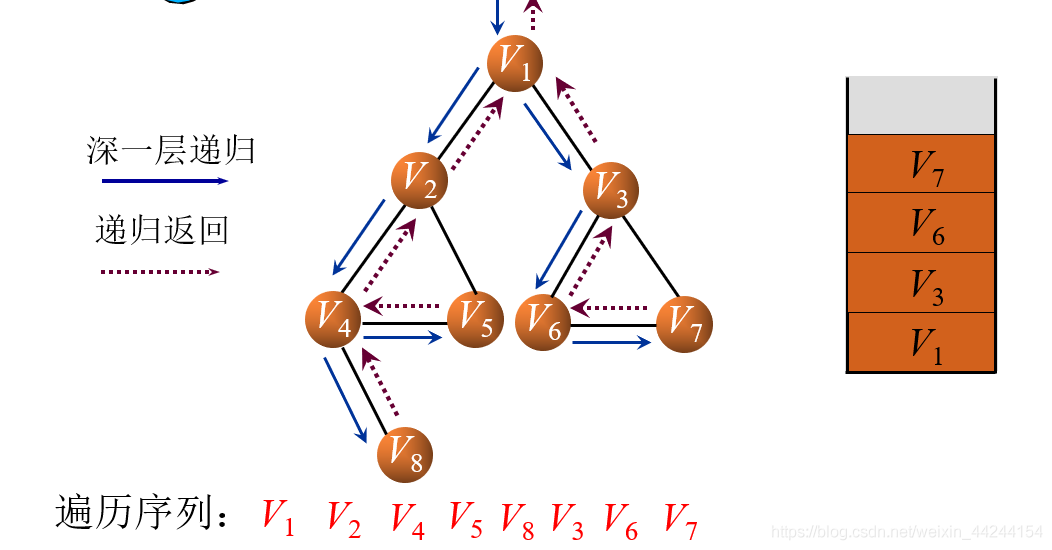
最后依次出栈,深度优先就遍历完了.
深度遍历代码
/**********深度优先遍历*********/
int visitDFS[maxSize];
void DFS(MGraph G,int i)
{
int j;
visitDFS[i] = 1;
printf("%d ", G.Vex[i]);
for (j = 0; j < G.vexnum; j++)
{
if (G.Edge[i][j] != 32767 && !visitDFS[j])
DFS(G, j);
}
}
void DFSTraverse(MGraph G)
{
int i;
for (i = 0; i < G.vexnum; i++)
visitDFS[i] = 0;
for (i = 0; i < G.vexnum; i++)
{
if (!visitDFS[i])
DFS(G, i);
}
深度遍历适用哪些问题的求解
1.求无向图的连通分量的个数
2.连通分量都包含哪些顶点
3.两个顶点是否在同一个连通分量中
4.单源路径问题
5.检测无向图中的环
1.2.2 广度优先遍历
在最开始时,V1入列,然后出列输出
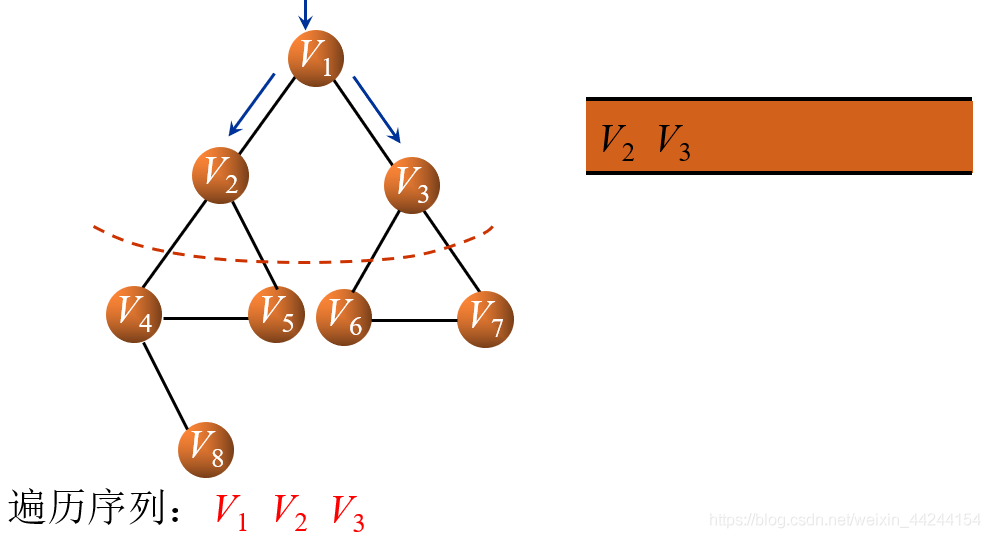
紧接着,与V1相连的结点有V2和V3,因此V2和V3入列并输出
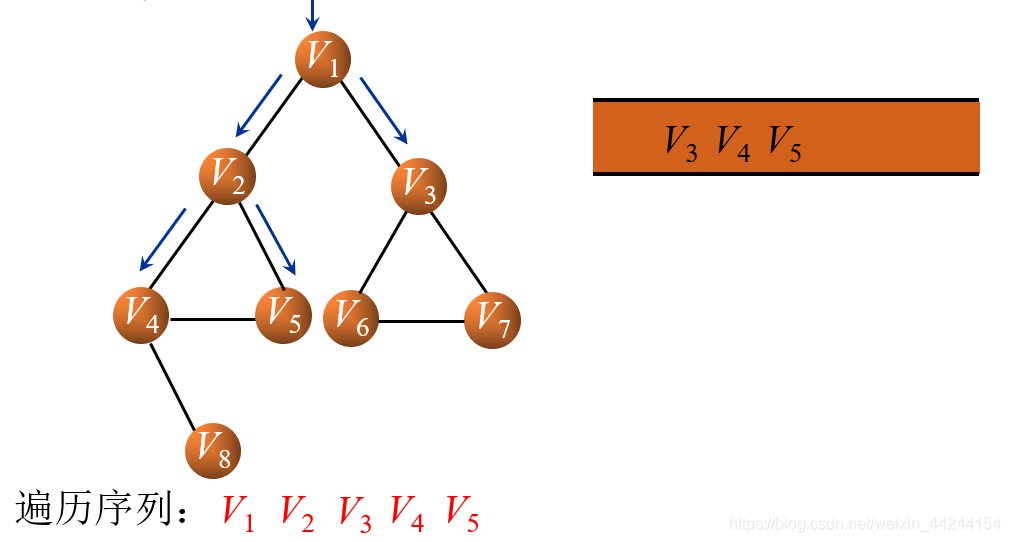
接下来V2出列,与V2相连的结点有V4和V5,所以V4和V5入列并输出
接下来同理,V3出列,V6和V7入列并输出

然后V4出列,与V4相连的还有V8,所以V8入列并输出

这样就遍历完了,后面的结点由于相邻结点都被访问过了,因此可以直接出列。
广度遍历代码
//广度优先遍历
int visitBFS[maxSize];
void BFS(MGraph G)
{
int i, j;
Queue Q;
for (i = 0; i < G.vexnum; i++)
visitBFS[maxSize] = 0;
InitQueue(&Q);
for (i = 0; i < G.vexnum; i++)
{
if (!visitBFS[i])
{
visitBFS[i] = 1;
printf("%d ", G.Vex[i]);
EnQueue(&Q, i);
while (!IsEmpty(&Q))
{
DeQueue(&Q, &i);
for (j = 0; j < G.vexnum; j++)
{
if (!visitBFS[j] && G.Edge[i][j] != 32767)
{
visitBFS[j] = 1;
printf("%d ", G.Vex[j]);
EnQueue(&Q, j);
}
}
}
}
}
}
广度遍历适用哪些问题的求解。
BFS 的应用一:层序遍历
BFS 的应用二:最短路径
1.3 最小生成树
用自己语言描述什么是最小生成树。
我认为最小生成树就是边的权值最小的生成树
1.3.1 Prim算法求最小生成树
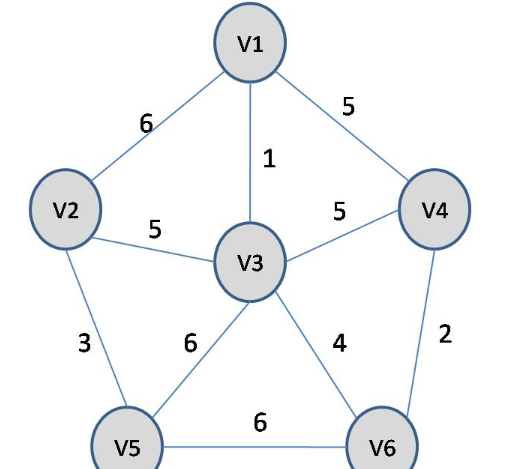
基于上述图结构求Prim算法生成的最小生成树的边序列

Prim算法思想:
逐渐长成一棵最小生成树。假设G=(V,E)是连通无向网,T=(V,TE)是求得的G的最小生成树中边的集合,U是求得的G的最小生成树所含的顶点集。初态时,任取一个顶点u加入U,使得U={u},TE=Ø。重复下述操作:找出U和V-U之间的一条最小权的边(u,v),将v并入U,即U=U∪{v},边(u,v)并入集合TE,即TE=TE∪{(u,v)}。直到V=U为止。最后得到的T=(V,TE)就是G的一棵最小生成树。也就是说,用Prim求最小生成树是从一个顶点开始,每次加入一条最小权的边和对应的顶点,逐渐扩张生成的。
实现Prim算法的2个辅助数组是什么?其作用是什么?Prim算法代码。
设置2个辅助数组:
1.closest[i]:最小生成树的边依附在U中顶点编号。
2.lowcost[i]表示顶点i(i ∈ V-U)到U中顶点的边权重,取最小权重的顶点k加入U。
并规定lowcost[k]=0表示这个顶点在U中
每次选出顶点k后,要队lowcost[]和closest[]数组进行修正
//最小生成树-Prim算法
void Prim(Graph G)
{
int v=0;//初始节点
closedge C[MaxVerNum];
int mincost = 0; //记录最小生成树的各边权值之和
//初始化
for (int i = 0; i < G.vexnum; i++)
{
C[i].adjvex = v;
C[i].lowcost = G.Edge[v][i];
}
cout << "最小生成树的所有边:"<< endl;
//初始化完毕,开始G.vexnum-1次循环
for (int i = 1; i < G.vexnum; i++)
{
int k;
int min = INF;
//求出与集合U权值最小的点 权值为0的代表在集合U中
for (int j = 0; j<G.vexnum; j++)
{
if (C[j].lowcost != 0 && C[j].lowcost<min)
{
min = C[j].lowcost;
k = j;
}
}
//输出选择的边并累计权值
cout << "(" << G.Vex[k] << "," << G.Vex[C[k].adjvex]<<") ";
mincost += C[k].lowcost;
//更新最小边
for (int j = 0; j<G.vexnum; j++)
{
if (C[j].lowcost != 0 && G.Edge[k][j]<C[j].lowcost)
{
C[j].adjvex = k;
C[j].lowcost= G.Edge[k][j];
}
}
}
cout << "最小生成树权值之和:" << mincost << endl;
分析Prim算法时间复杂度,适用什么图结构?
Prim算法的时间复杂度是O(n^2)的,因此适用于稠密图的最小生成树
1.3.2 Kruskal算法求解最小生成树
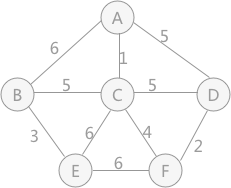
基于上述图结构求Kruskal算法生成的最小生成树的边序列
首先,在初始状态下,对各顶点赋予不同的标记(用颜色区别),如下图所示:

对所有边按照权值的大小进行排序,按照从小到大的顺序进行判断,首先是(1,3),由于顶点 1 和顶点 3 标记不同,所以可以构成生成树的一部分,遍历所有顶点,将与顶点 3 标记相同的全部更改为顶点 1 的标记,如下图所示:
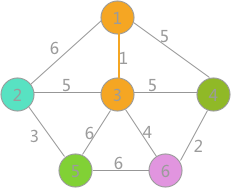
其次是(4,6)边,两顶点标记不同,所以可以构成生成树的一部分,更新所有顶点的标记为:
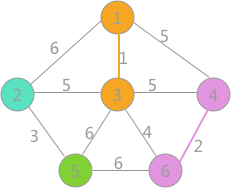
其次是(2,5)边,两顶点标记不同,可以构成生成树的一部分,更新所有顶点的标记为
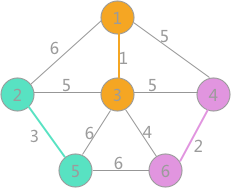
然后最小的是(3,6)边,两者标记不同,可以连接,遍历所有顶点,将与顶点 6 标记相同的所有顶点的标记更改为顶点 1 的标记:
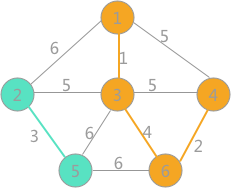
继续选择权值最小的边,此时会发现,权值为 5 的边有 3 个,其中(1,4)和(3,4)各自两顶点的标记一样,如果连接会产生回路,所以舍去,而(2,3)标记不一样,可以选择,将所有与顶点 2 标记相同的顶点的标记全部改为同顶点 3 相同的标记:

选取的边的数量相比与顶点的数量小 1 时,说明最小生成树已经生成
实现Kruskal算法的辅助数据结构是什么?其作用是什么?Kruskal算法代码。
实现Kruskal算法的辅助数据结构是vset[]。vset[]用于判断顶点i,j是否属于同一个连通分量。
//最小生成树-Kruskal算法
void Kruskal(Graph G)
{
//初始化
sort(l.begin(), l.end(),cmp);
int verSet[MaxVerNum];
int mincost = 0;
for (int i = 0; i < G.vexnum; i++)
verSet[i] = i;
cout << "最小生成树所有边:" << endl;
//依次查看边
int all = 0;
for (int i = 0; i < G.arcnum; i++)
{
if (all == G.vexnum - 1)break;
int v1 = verSet[l[i].from];
int v2 = verSet[l[i].to];
//该边连接两个连通分支
if (v1 != v2)
{
cout << "(" << l[i].from << "," << l[i].to << ") ";
mincost += l[i].weight;
//合并连通分支
for (int j = 0; j < G.vexnum; j++)
{
if (verSet[j] == v2)verSet[j] = v1;
}
all++;
}
}
cout << "最小生成树权值之和:" <<mincost<<endl;
分析Kruskal算法时间复杂度,适用什么图结构?
时间复杂度为O(eloge)。和普里姆算法恰恰相反,更适合于求稀疏图的最小生成树。
1.4 最短路径
1.4.1 Dijkstra算法求解最短路径
迪杰斯特拉(Dijkstra)算法是典型最短路径算法,用于计算一个节点到其他节点的最短路径。
它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想),直到扩展到终点为止
基于上述图结构,求解某个顶点到其他顶点最短路径。(结合dist数组、path数组求解)
1.狄克斯特拉(Dijkstra)算法
过程:
S={入选顶点集合,初值V0},T={未选顶点集合}。
若存在<V0,Vi>,距离值为<V0,Vi>弧上的权值
若不存在<V0,Vi>,距离值为∞
从T中选取一个其距离值为最小的顶点W, 加入S
S中加入顶点w后,对T中顶点的距离值进行修改:重复上述步骤1,直到S中包含所有顶点,即S=V为止。
重复上述步骤1,直到S中包含所有顶点,即S=V为止。
图解:

Dijkstra算法需要哪些辅助数据结构
void Dijkstra(MGraph g, int v)//源点v到其他顶点最短路径
{
int dist[MAXV], path[MAXV],s[MAXV];
int mindistance,u;//u为每次所选最短路径点
for (int i = 0; i < g.n; i++)//初始化各数组
{
s[i] = 0;//初始已选入点置空
dist[i] = g.edges[v][i];//初始化最短路径
if (dist[i] < INF) path[i] = v;
else path[i] = -1;//即无直接到源点V的边,因此初始化为-1
}
s[v] = 1;//源点入表示已选
for (int j = 0; j < g.n; j++)//要将所有点都选入需循环n-1次
{
mindistance = INF;//每次选之前重置最短路径
for (int i = 1; i < g.n; i++)//每次都遍历源点以外其他点来选入点
{
if (s[i] == 0 && dist[i] < mindistance)//在未选的点中找到最短路径
{
mindistance = dist[i];
u = i;//u记录选入点
}
}
s[u] = 1;//最后记录的u才为最后选入点
for (int i = 1; i < g.n; i++)//修正数组值
{
if (s[i] == 0)//!!仅需修改未被选入点的,已选入的既定
{
if (g.edges[u][i] < INF && dist[u] + g.edges[u][i] < dist[i])//先判断选入点到与该点存在时再比较判断
{
dist[i] = dist[u] + g.edges[u][i];
path[i] = u;
}
}
}
}
Dispath(dist, path, s, g.n, v);
}
Dijkstra算法的时间复杂度,使用什么图结构,为什么?
Dijkstra算法 适用于求 稠密图 的最短路问题,因为 稠密图 的边数远远大于点数,Dijkstra算法的思路为进行 n 次循环,每次循环再遍历 n 个点确定一个还未确定最短距离的点中距离源点最近距离的点,然后再用这个点更新其所能到达的点(算法默认当前的点可以到达所有的点,因为没有到达的点之间的距离都已经初始化为正无穷大,所以不会被更新,不影响结果)。时间复杂度为 O(n2)。
1.4.2 Floyd算法求解最短路径
Floyd算法解决什么问题?
Floyd算法(Floyd-Warshall algorithm)又称为弗洛伊德算法、插点法,是解决给定的加权图中顶点间的最短路径的一种算法,可以正确处理有向图或负权的最短路径问题,同时也被用于计算有向图的传递闭包。
Floyd算法需要哪些辅助数据结构
void Floyd(Graph G)
{
int A[MAXVEX][MAXVEX]; //建立A数组
int path[MAXVEX][MAXVEX]; //建立path数组
int i, j, k;
for (i=0;i<G.n;i++)
for (j=0;j<G.n;j++)
{
A[i][j]=G.edges[i][j];
if (i!=j && G.edges[i][j]<INF)
path[i][j]=i; //i和j顶点之间有一条边时
else
path[i][j]=-1;
}
for (k=0;k<G.n;k++) //求Ak[i][j]
{
for (i=0;i<G.n;i++)
for (j=0;j<G.n;j++)
if (A[i][j]>A[i][k]+A[k][j]) //找到更短路径
{
A[i][j]=A[i][k]+A[k][j]; //修改路径长度
path[i][j]=path[k][j]; //修改最短路径为经过顶点k
}
}
}
1.两个二维数组
2.邻接矩阵
Floyd算法优势
Floyd算法适用于APSP(AllPairsShortestPaths),是一种动态规划算法,稠密图效果最佳,边权可正可负。此算法简单有效,由于三重循环结构紧凑,对于稠密图,效率要高于执行|V|次Dijkstra算法。
优点:容易理解,可以算出任意两个节点之间的最短距离,代码编写简单
缺点:时间复杂度比较高,不适合计算大量数据。
1.5 拓扑排序
拓扑排序指的是将有向无环图(又称“DAG”图)中的顶点按照图中指定的先后顺序进行排序。
找一个有向图,并求其对要的拓扑排序序列
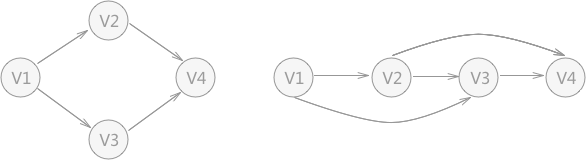
对有向无环图进行拓扑排序,只需要遵循两个原则:
1.在图中选择一个没有前驱的顶点 V;
2.从图中删除顶点 V 和所有以该顶点为尾的弧。
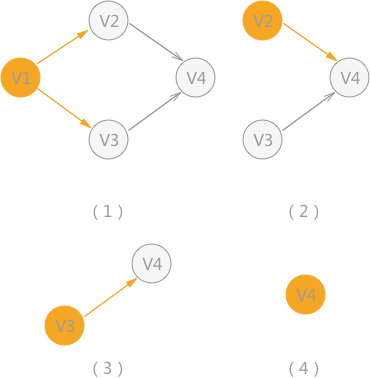
进行拓扑排序时,首先找到没有前驱的顶点 V1,如图 2(1)所示;在删除顶点 V1 及以 V1 作为起点的弧后,继续查找没有前驱的顶点,此时, V2 和 V3 都符合条件,可以随机选择一个,例如图 2(2) 所示,选择 V2 ,然后继续重复以上的操作,直至最后找不到没有前驱的顶点。
所以,针对图 2 来说,拓扑排序最后得到的序列有两种:
- V1 -> V2 -> V3 -> V4
- V1 -> V3 -> V2 -> V4
实现拓扑排序代码,结构体如何设计?
typedef struct {
Vertex data;//顶点信息
int count;//存放入度
AreNode *firstarc;//头结点类型
}VNode;
书写拓扑排序伪代码,介绍拓扑排序如何删除入度为0的结点?
while(栈不空)
{
出栈v,访问;
遍历v所有邻接点
{
所有邻接点的入度-1
当入度为0时,则入栈,以此实现入度为0时的删除操作
}
}
如何用拓扑排序代码检查一个有向图是否有环路?
DFS判断有向图是否有环
对一个节点u进行DFS,判断是否能从u回到自己这个节点,即是否存在u到u的回路。
color数组代表每个节点的状态
-1代表还没访问,0代表正在被访问,1代表访问结束
如果一个状态为0的节点,与它相连的节点状态也为0,则有环
1.6 关键路径
什么叫AOE-网?
AOE网(Activity On Edge)即边表示活动的网,是与AOV网(顶点表示活动)相对应的一个概念。而拓扑排序恰恰就是在AOV网上进行的,这是拓扑排序与关键路径最直观的联系。AOE网是一个带权的有向无环图,其中顶点表示事件(Event),弧表示活动,权表示活动持续的时间。
什么是关键路径概念?
在项目管理中,关键路径是指网络终端元素的元素的序列,该序列具有最长的总工期并决定了整个项目的最短完成时间。
求关键路径必须在拓扑排序的前提下进行,有环图不能求关键路径; (2) 只有缩短关键活动的工期才有可能缩短工期; (3) 若一个关键活动不在所有的关键路径上,减少它并不能减少工期; (4) 只有在不改变关键路径的前提下,缩短关键活动才能缩短整个工期。
什么是关键活动?
关键活动是为准时完成项目而必须按时完成的活动。即处于关键路径上的活动。所有项目都是由一系列活动组成,而在这些活动中存在各种链接关系和活动约束。其中有些活动如果延误就会影响整个项目工期。在项目中总存在这样一类直接影响项目工期变化的活动,这些活动就是关键活动。
2.PTA实验作业
2.1 六度空间

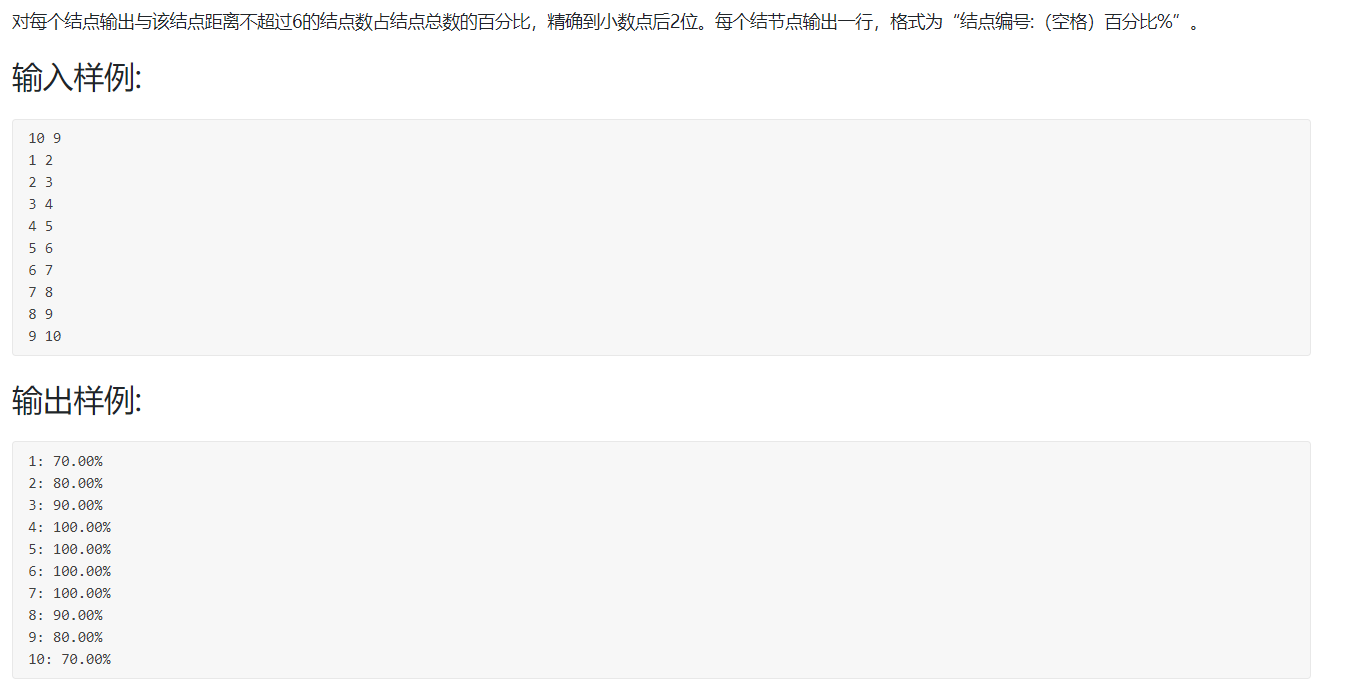
2.1.1 伪代码
宏定义邻接矩阵g[10001][10001],顶点数v,边数e,循环变量i,中间变量x,y用来输入
main函数
定义浮点型数据 n,m来求最后所占比率
输入顶点数v和边数e
while e-- //构建邻接矩阵
输入边关系 x y
g[x][y] = g[y][x] = 1
end while
for i=1 to v do
n=v
m=bfs(i) //调用bfs函数
end for
return 0
int bfs(int z)
定义数组vis[10001]=0 表示是否被访问过的结点
定义 last = z表示记录每层的最后一个元素
i定义tail表示用于记录每一层压入栈时的结点
定义 level = 0 表示与该结点距离是否为6
定义count=1//表示结点
创建int型栈q并入栈z
将vis[z]置为1表示访问过了
while q不为空
z = q.front()//取栈顶元素于z
q.pop()//去栈顶
for i = 1to v do //广度遍历方法
if g[z][i] 等于1 并且 vis[i]等于 0 then
count++;
vis[i] = 1;
q.push(i);
tail = i;
end if
end for
if last 等于z then//一层全部从栈弹出,准备开始弹下一层,弹出的数等于当前层最后一个元素,并记录与last
level++;
last = tail;//记录最后一个元素
end if
if level 等于 6 break //符合题意的路径节点
return count
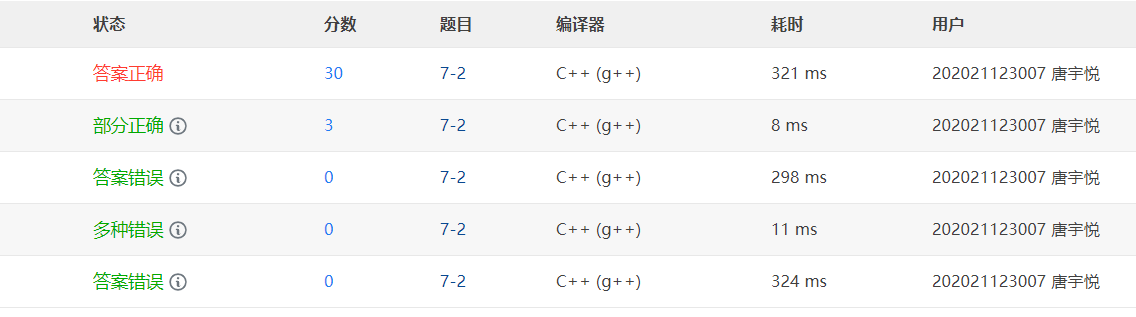
2.1.2 提交列表
2.1.3 本题知识点
1.图的广度遍历方法
2.栈的方法
3.使用了创建邻接矩阵方法
2.2 村村通
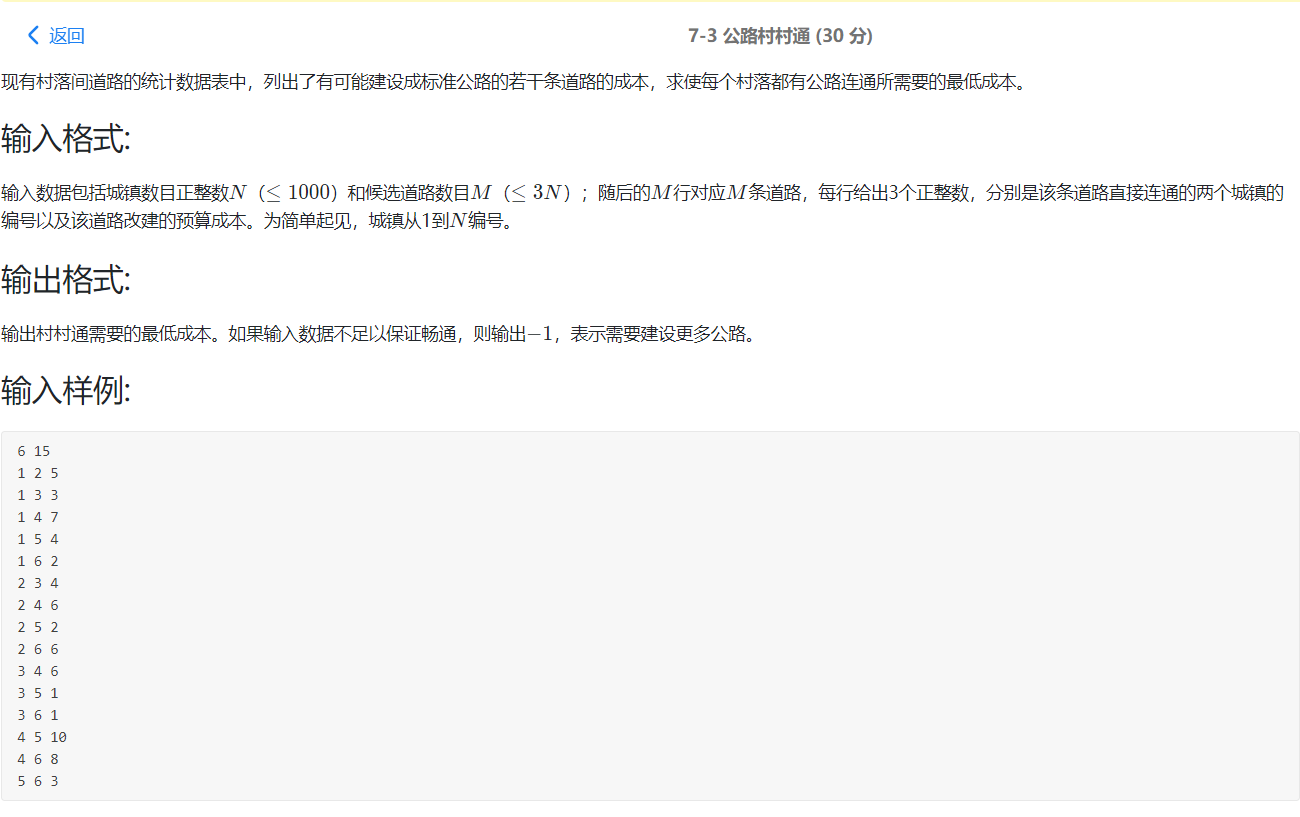

2.2.1 伪代码
用边存储结构读取数据
初始化vset数组使各数的起始节点设为本身
while k记录已保存的边数目!=顶点数-1
寻找权值最小的边
if 该边的权值为极大值
图不连通 输出-1并退出循环
寻找这边始末节点的起始节点
if 起始节点不相等
将其中一边的起始节点的起始节点记录为另一边的起始节点
记录权值
将该边的权值设为极大值
if 记录的边数=顶点数-1
输出权值的和
2.2.2 提交列表

2.2.3 本题知识点
1.利用了prim最小生成树方法
2.邻接矩阵用法