实验四 图的实现与应用
目录
实验一
实验二
实验三
实验一
题目
用邻接矩阵实现无向图(边和顶点都要保存),实现在包含添加和删除结点的方法,添加和删除边的方法,size(),isEmpty(),广度优先迭代器,深度优先迭代器
给出伪代码,产品代码,测试代码(不少于5条测试)
上方提交代码链接
附件提交测试截图
分析
首先要先复习一下有关无向图的邻接矩阵的表示方法,因为要保存图的顶点与边所以要选择一种数据结构来保存顶点与边,对于顶点来说比较的好保存一些,可以用ArrayList来存储,对于点来说就比较的复杂,就要用到数组来保存,实际上二维数组就可已构成一个矩阵,如果边存在就将相应的位置的数据变为1,不是则还是原来的null。广度优先迭代器要用到队列,深度优先迭代器需要用到栈,这就是在开始之前做好的数据结构的选择。其他几项都是在这几个数据结构的计出上来进一步操作来完成的。
代码链接
问题与解决
1.递归的问题,在遍历的时候就用到了如图的方法来遍历,但是在进行测试的时候发现少了很多元素,经过单步追踪发现在进行递归之前的数据在进行下一次递归的时候都会被清楚,所以导致了很多数据的丢失,问题就出在对列声明的位置不对,在递归的方法内每次都会被重新的定义一遍也就导致了数据的丢失,所以要在递归的方法之外就定义一个队列,然后以参数的形式出入,这样每次递归之后的数据都进入到对列中,而不会丢失了,这一点与循环比较相似。同时由于这个方法的部分递归部分不能参与递归所以就不得不将其拆分为两个方法来实现。
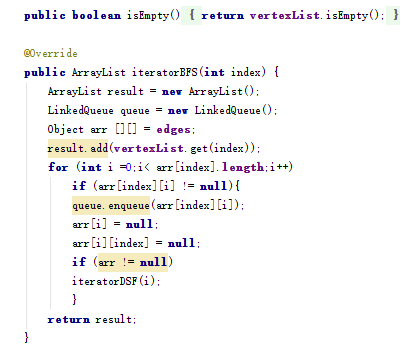
private LinkedQueue BFS(Object[][] arr,LinkedQueue queue, int index){
for (int ai = 0;ai<arr.length;ai++){
arr[ai][index] = null;
}
for (int i =0;i< arr[index].length;i++)
if (arr[index][i] != null){
arr[index][i] = null;
arr[i][index] = null;
queue.enqueue(vertexList.get(i));
for (int ai = 0;ai< edges.length;ai++) {
arr[ai][i] = null;
}
arr[i][index] = null;
if (arr != null)
BFS(arr,queue,i);
}
return queue;
}
2.在删除顶点之后边的数目的变化,原先只是将顶点删除就没有注意要将边的数目也要相应的变小。所以在测试的时候一直出现问题,因为删除顶点是在遍历列表的基础上进行的,所以只有在真的删除了元素之后才能减少边的个数。
if (vertexList.contains(e) == false)
System.out.println("没有该元素");
else {
int a = vertexList.indexOf(e);
vertexList.remove(a);
for (int ai = 0;ai< edges[a].length;ai++){
if ( edges[a] [ai]!= null){
edges[a] [ai]= null;
EdgesCont--;
}
}
截图
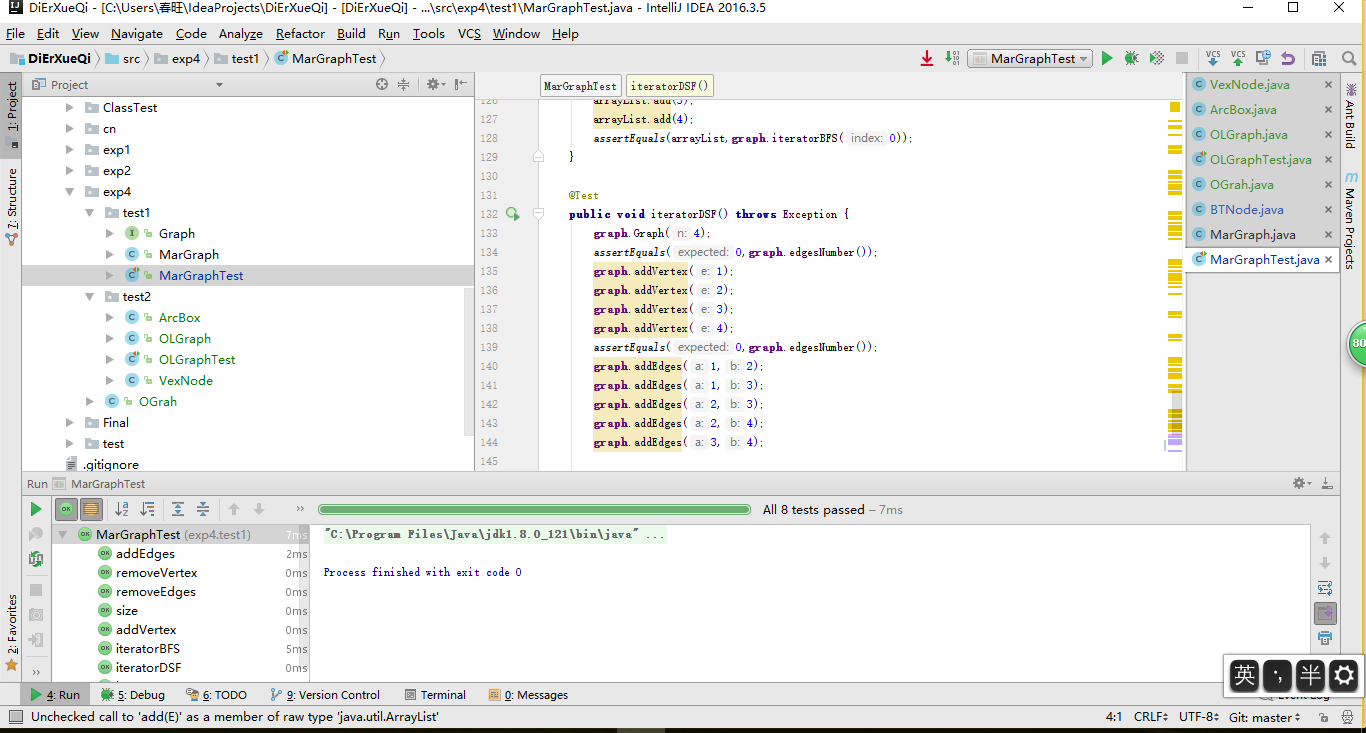
代码链接
返回目录
实验二
题目
用十字链表实现无向图(边和顶点都要保存),实现在包含添加和删除结点的方法,添加和删除边的方法,size(),isEmpty(),广度优先迭代器,深度优先迭代器
给出伪代码,产品代码,测试代码(不少于5条测试)
上方提交代码链接
附件提交测试截图
分析
对于数据结构是使用大致与实现邻接矩阵的时候是相似的,只是在表示边的时候要将原先用二维数组实现的改为用列表来表示。
问题
对于出现的问题大多都是在上一个程序中出现的问题,唯一不同的就是在进行边的建立时的问题还是比较的多,所以参考在实现队列栈等数据结构时课本上的数据结构,我就选用了EdgeNode的类来实现。同时也将创建顶点方法也独立出来了。
public class EdgeNode<T> {
T data;
int head;
int tail;
EdgeNode sameHeadVertex;
EdgeNode sameTailVertex;
public EdgeNode(T data, int From, int To) {
this.data = data;
this.head = From;
this.tail = To;
}
}
public class VertexNode <T>{
T data;
EdgeNode<T> InEdge;
EdgeNode<T> OutEdge;
public void Vertex(T data) {
this.data = data;
}
}
总结
在实现方法的时候我们先要有大致的思路,除非在实在行不通的情况下要不然就不要去轻易的改变思路,只会让你的思路越来越乱,分不清东西南北。
截图
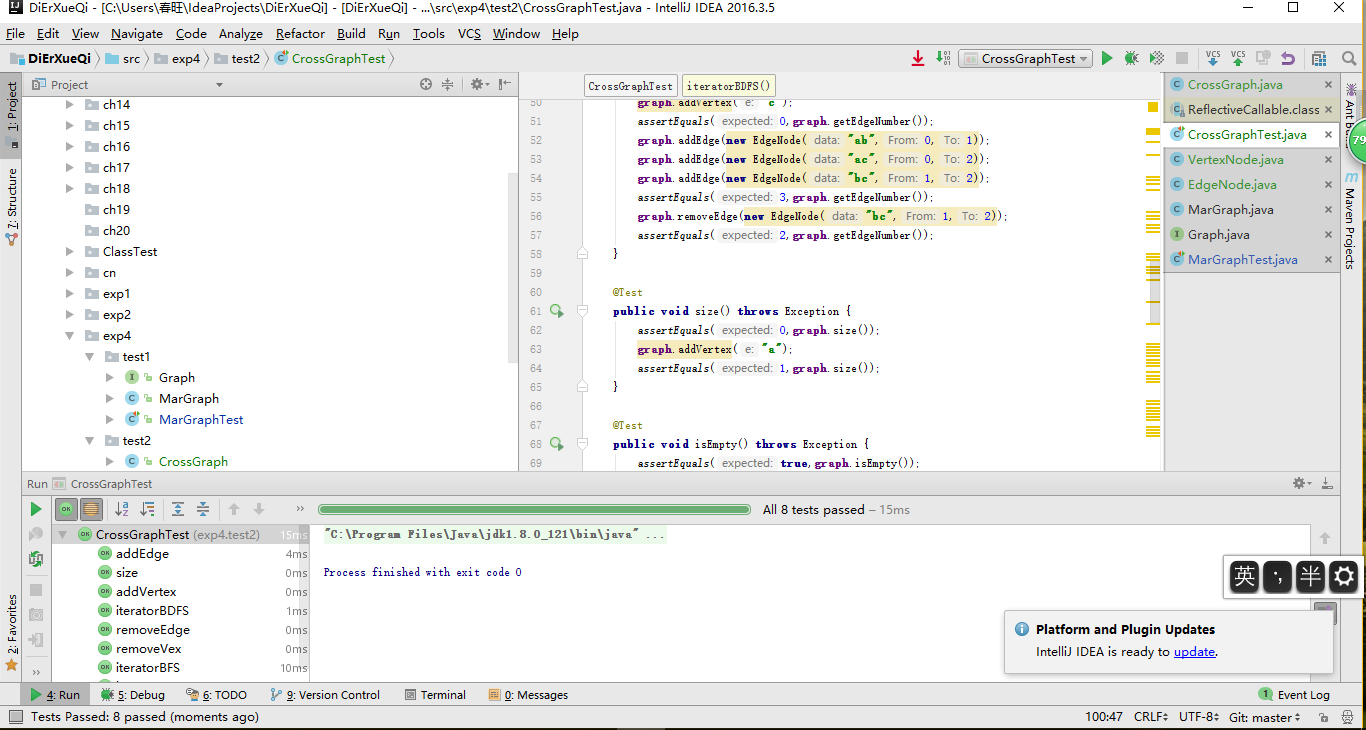
代码链接
返回目录
实验三
题目
实现PP19.9
给出伪代码,产品代码,测试代码(不少于5条测试)
上方提交代码链接
附件提交测试截图
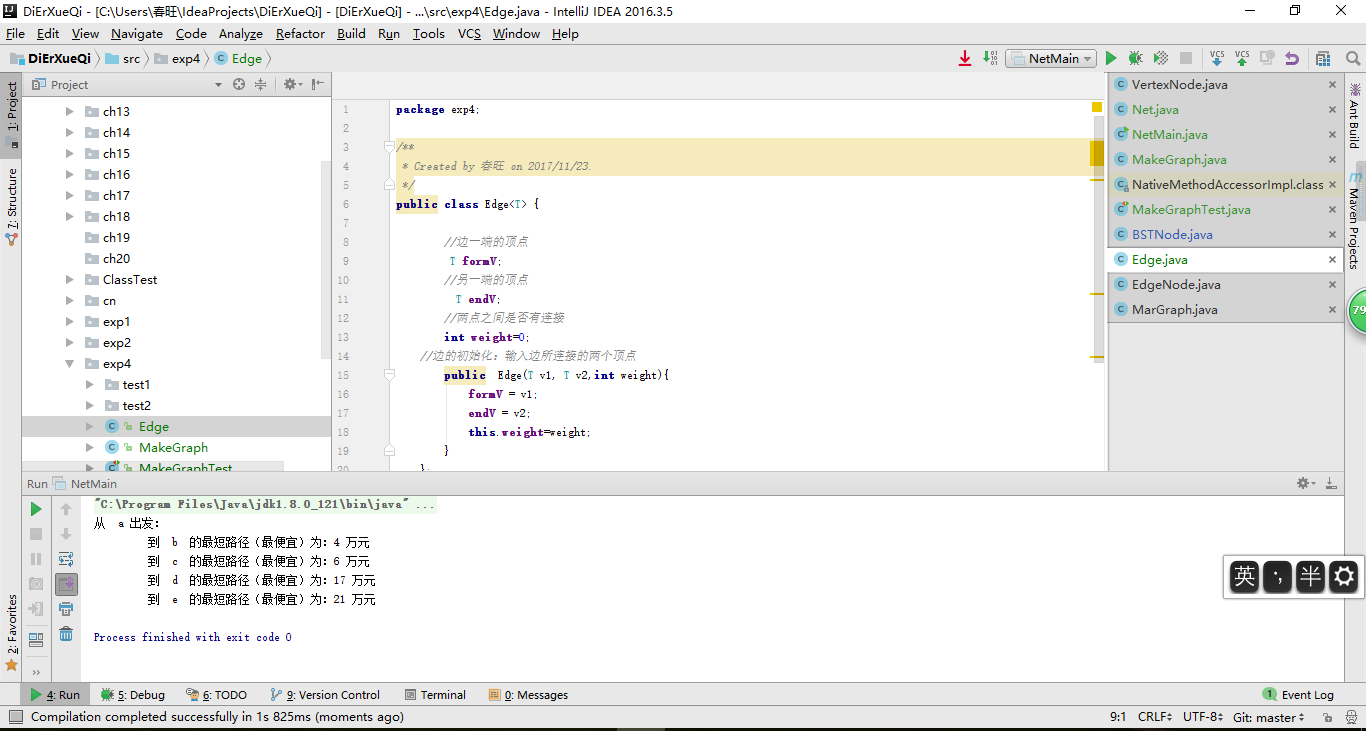
PP19.9 创建计算机网络路由系统,输入网络中点到点的线路,以及每条线路的使用费用,系统输出网络中各点之间最便宜的路径,指出不相通的所有的位置。
分析
- 1.首先因为要输入点到点之间的线路所以要创建一个可以构造一个构造图的方法,但是又因为要输入每条线路的使用费用,所以构造的图要是有权图。所以要有一个类构造一个有权图。
- 2.其次要可以输出点到点之间的最便宜的路径,就要创建一个可以寻找有权图最短路径的方法。
- 3.最后一步是测试自己构建一个图来测试先前写好的两个类在实际运行环境下的变化。
问题
在创建边的时候我是先让方法找到开始的顶点,之后再去找结束的顶点但是在进行整体的测试时出现了找不到已经加进去的顶点的问题,所以我不得不给添加边的方法又单独写了一个测试类来进行单步追踪,终于找到原因,我将顶点在列表中的位置与顶点中的位置产生了混淆,所以导致了我输入的元素与找的元素连数据类型都不一样,所以就产生了这样的问题。
对于添加的边的测试如下图:
package exp4.test3;
import org.junit.Test;
/**
* Created by 春旺 on 2017/11/24.
*/
public class MakeGraphTest {
@Test
public void addEdged() throws Exception {
MakeGraph graph = new MakeGraph();
graph.addVex("a");
graph.addVex("b");
graph.addVex("c");
graph.addVex("d");
graph.addVex("e");
Edge edge1 = new Edge(0,4,5);
Edge edge2 = new Edge(0,1,4);
Edge edge3 = new Edge(0,2,6);
Edge edge4 = new Edge(1,4,10);
Edge edge5 = new Edge(4,2,15);
Edge edge6 = new Edge(1,3,13);
Edge edge7 = new Edge(4,3,2);
Edge edge8 = new Edge(2,3,25);
graph.addEdged(edge1);
graph.addEdged(edge2);
graph.addEdged(edge3);
graph.addEdged(edge4);
graph.addEdged(edge5);
graph.addEdged(edge6);
graph.addEdged(edge7);
graph.addEdged(edge8);
}
}
代码链接
截图