哈夫曼树 数据结构课程

让使用频率高的(权值高)节点离根部更近,生成一个哈夫曼树。

具体算法为：1输入各节点权重，把每一个节点当成一课子树，从而得到一片森林

　　　　　　2从森林中寻找权值最小的两棵树，把他们合并为一课新的树，树的权值为原来这两棵子树的权值之和

　　　　　　3不断进行第二步，直到把森林合并为一个树时停止

这样就可以生成一棵哈夫曼树，然后每个叶节点向根部回溯，根据节点来自左右子树编码0/1,到达根节点时就得到了每个叶节点的哈夫曼编码。

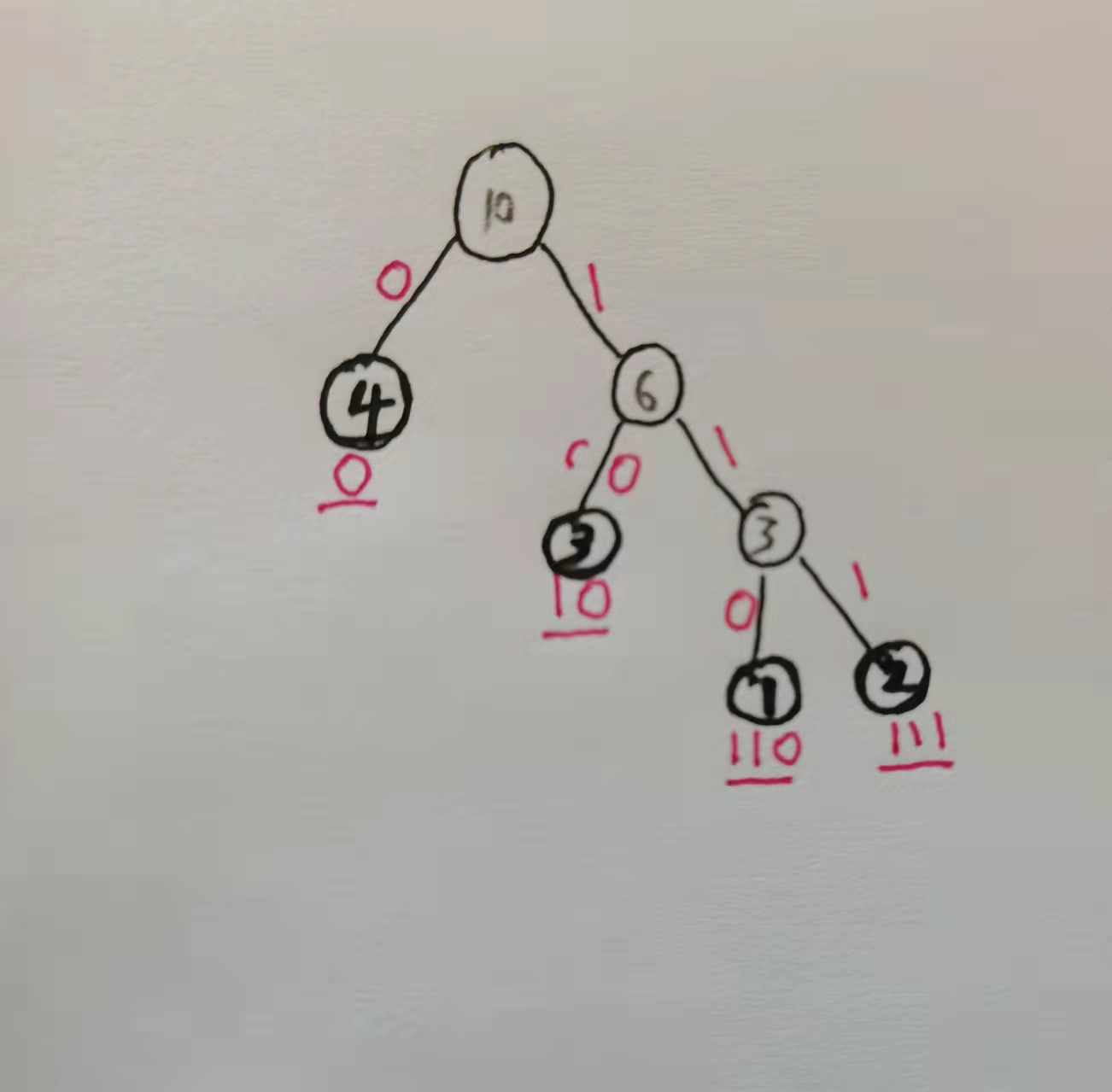
举个栗子： 输入四个节点，权重分别为1,2,3,4.

step1：权值最小的两个子树为，1,2  把他们合并为权值为3的树 （此时，森林为3,3,4）

step2：权值最小的两个子树为，3,3  把他们合并为权值为6的树 （此时森林为6,4）

step3：权值最小的两个子树为，6,4  把他们合并为权值为10的树 (此时森林为10，只有一棵树)

这样就得到了哈夫曼树。如图。

#include<cstdio>
#include<cstring>
#include<malloc.h>
#include<iostream>
using namespace std;
const int N=100;
typedef struct//节点类型 
{
    char data;
    int weight;
    int parent;
    int lchild;
    int rchild;
}HTNode,*HuffmanTree;
typedef struct//哈夫曼编码类型 
{
    char bit[N];
    int start;
}HCode_Node;
void CreateHTCode(HTNode HTree[],HCode_Node HCode[],int n)
{
    
    int i,f,c;
    HCode_Node hc;
    for(i=1;i<=n;i++)
    {
        hc.start=n;
        c=i;
        f=HTree[i].parent;
        while(f)//对每个节点通过迭代寻找父节点 编码哈夫曼编码 
        {
            if(HTree[f].lchild==c)
                hc.bit[--hc.start]='0';
            else 
                hc.bit[--hc.start]='1';
                c=f;
                f=HTree[f].parent;
        }
        HCode[i]=hc;
    }
}
void DisplayHuffmanCode(HTNode HTree[],HCode_Node HCode[],int n)
{
    
    int i,k;
    printf(" 输出哈夫曼编码
");
    for(i=1;i<=n;i++)
    {
        //printf("start ==%d
",HCode[i].start);
        for(k=0;k<HCode[i].start;k++)
            printf(" ");
        for(k=HCode[i].start;k<n;k++)
            printf("%c",HCode[i].bit[k]);
        printf("
");
    }
}
void Select(HuffmanTree &HT,int len,int &s1,int &s2)
{
    int i,min1=0xffff,min2=0xffff;
    for(i=1;i<=len;i++)
    {
        if(!HT[i].parent)
        {
            if(HT[i].weight <min1)
            {
                min2=min1;s2=s1;
                min1=HT[i].weight;s1=i;
            }else
            if(HT[i].weight <min2)
            {
                min2=HT[i].weight ;s2=i;
            }
        }
    }
    return;
}
void CreatHuffmanTree(HuffmanTree &HT,int n)
{
    int m,s1,s2,i;
    if(n<=1) return ;
    m=n*2-1;
    HT= new HTNode[m+1];//申请空间
    for(i=1;i<=m;i++)    
        HT[i].parent=HT[i].lchild=HT[i].rchild=0;//初始化变量 
    
    printf("请输入各节点的权值
");
    for(i=1;i<=n;i++)
        scanf("%d",&HT[i].weight);
    //开始构造 
    for(i=n+1;i<=m;i++)
    {
        Select(HT,i-1,s1,s2);//寻找权值最小的子树
        HT[s1].parent=i;
        HT[s2].parent=i;
        //合并权值最小的子树
        HT[i].lchild=s1;
        HT[i].rchild=s2;
        HT[i].weight =HT[s1].weight+HT[s2].weight;
    }
    
    HCode_Node HCode[N];//创建哈夫曼编码的数组 
    
    CreateHTCode(HT,HCode,n);
    DisplayHuffmanCode(HT,HCode,n);
    return;
}

int main()
{
    HuffmanTree HT;int n;
    printf("请输入节点个数
");
    scanf("%d",&n);
    CreatHuffmanTree(HT,n);
    return 0;
    
}