1.本节重点知识点用自己的话总结出来,可以配上图片,以及说明该知识点的重要性
线性:两个变量之间的关系是一次函数关系的——图象是直线,叫做线性
非线性:两个变量之间的关系不是一次函数关系的——图象不是直线,叫做非线性。
回归:人们在测量事物的时候因为客观条件所限,求得的都是测量值,而不是事物真实的值,为了能够得到真实值,无限次的进行测量,最后通过这些测量数据计算回归到真实值,这就是回归的由来。
对大量的观测数据进行处理,从而得到比较符合事物内部规律的数学表达式。也就是说寻找到数据与数据之间的规律所在,从而就可以模拟出结果,也就是对结果进行预测。解决的就是通过已知的数据得到未知的结果。例如:对房价的预测、判断信用评价、电影票房预估等。
一般表达式:
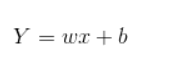
2.思考线性回归算法可以用来做什么?(大家尽量不要写重复)
1. 趋势线,一组特定数据(如GDP、石油价格和股票价格)是否在一段时期内增长或下降。虽然我们可以用肉眼观察数据点在坐标系的位置大体画出趋势线,更恰当的方法是利用线性回归计算出趋势线的位置和斜率。
2.流行病学,有关吸烟对死亡率和发病率影响的早期证据来自采用了回归分析的观察性研究。为了在分析观测数据时减少伪相关,除最感兴趣的变量之外,通常研究人员还会在他们的回归模型里包括一些额外变量。例如,假设我们有一个回归模型,在这个回归模型中吸烟行为是我们最感兴趣的独立变量,其相关变量是经数年观察得到的吸烟者寿命。例如,某种不存在的基因可能会增加人死亡的几率,还会让人的吸烟量增加。因此,比起采用观察数据的回归分析得出的结论,随机对照试验常能产生更令人信服的因果关系证据。当可控实验不可行时,回归分析的衍生,如工具变量回归,可尝试用来估计观测数据的因果关系。
3.金融,资本资产定价模型利用线性回归以及Beta系数的概念分析和计算投资的系统风险。这是从联系投资回报和所有风险性资产回报的模型Beta系数直接得出的。
4.经济学,线性回归是经济学的主要实证工具。例如,它是用来预测消费支出,固定投资支出,存货投资,一国出口产品的购买,进口支出,要求持有流动性资产,劳动力需求、劳动力供给。
3.自主编写线性回归算法 ,数据可以自己造,或者从网上获取。(加分题)
代码:
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
import matplotlib.pyplot as plt
from sklearn.pipeline import Pipeline
from sklearn.exceptions import ConvergenceWarning
import matplotlib as mpl
mpl.rcParams['font.sans-serif'] = [u'simHei']
mpl.rcParams['axes.unicode_minus'] = False
import warnings
warnings.filterwarnings(action='ignore', category=ConvergenceWarning)
np.random.seed(0)
np.set_printoptions(linewidth=1000)
N = 7
x = np.linspace(0, 6, N) + 0.5 * np.random.randn(N)
x = np.sort(x)
y = x ** 2 - 4 * x - 3 + 2 * np.random.randn(N)
x.shape = -1, 1 # 将一维转换成二维
y.shape = -1, 1
model = Pipeline([('poly', PolynomialFeatures()), ('linear', LinearRegression(fit_intercept=False))])
np.set_printoptions(suppress=True)
plt.figure(figsize=(15, 12), facecolor='w')
d_pool = np.arange(1, N, 1) # 阶
m = d_pool.size
title = '简单线性回归'
plt.figure(figsize=(12, 10), facecolor='w')
plt.plot(x, y, 'ro', ms=20, zorder=N)
for i, d in enumerate(d_pool):
print()
model.set_params(poly__degree=d)
model.fit(x, y.ravel())
lin = model.get_params('linear')['linear']
output = '%s:%d阶,系数为:' % (title, d)
print(output, lin.coef_.ravel()) # 偏置项和权重向量
x_hat = np.linspace(x.min(), x.max(), num=100)
x_hat.shape = -1, 1
y_hat = model.predict(x_hat)
s = model.score(x, y)
print('预测性能得分(其实就是R^2):', s, '
')
z = N - 1 if (d == 2) else 0
# z是下面画图中的zorder参数的值,是指该线在图中的级别,数值越大,级别越高,
# 在多线交叉时会显示在最上面,也就是会压住其他的线显示在最前面,这里是设置二阶拟合的级别最高
label = '%d阶,$R^2$=%.3f' % (d, s)
plt.plot(x_hat, y_hat, lw=5, alpha=1, label=label, zorder=z)
plt.legend(loc='upper left')
plt.grid(True)
plt.title(title, fontsize=18)
plt.xlabel('X', fontsize=16)
plt.ylabel('Y', fontsize=16)
plt.tight_layout(1, rect=(0, 0, 1, 0.95))
plt.suptitle('多项式曲线拟合比较', fontsize=22)
plt.show()
运行结果:
