21 遍历二叉树（三种遍历方式：左根右(中序)， 根左右(先序)， 左右根(后序)）

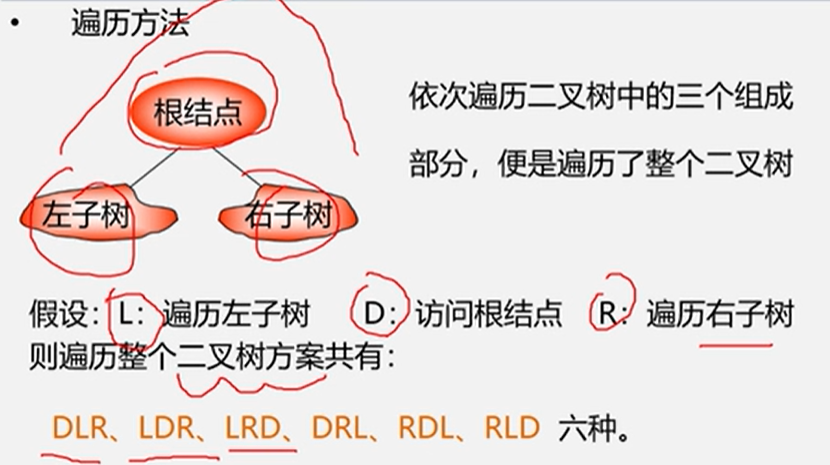
二叉树遍历：

　　顺着一条搜索路径访问二叉树中的节点，每个节点均被访问一次，且只被访问一次。

遍历目的：

　　得到树中所有节点的一个线性排列。

遍历用途：

　　是二叉树元素增删改查等操作的前提。

 

 

 

 

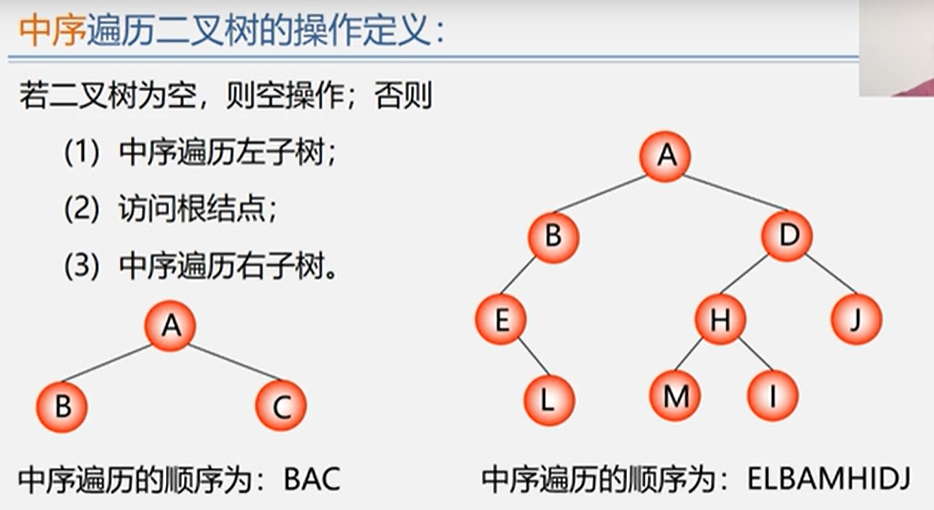
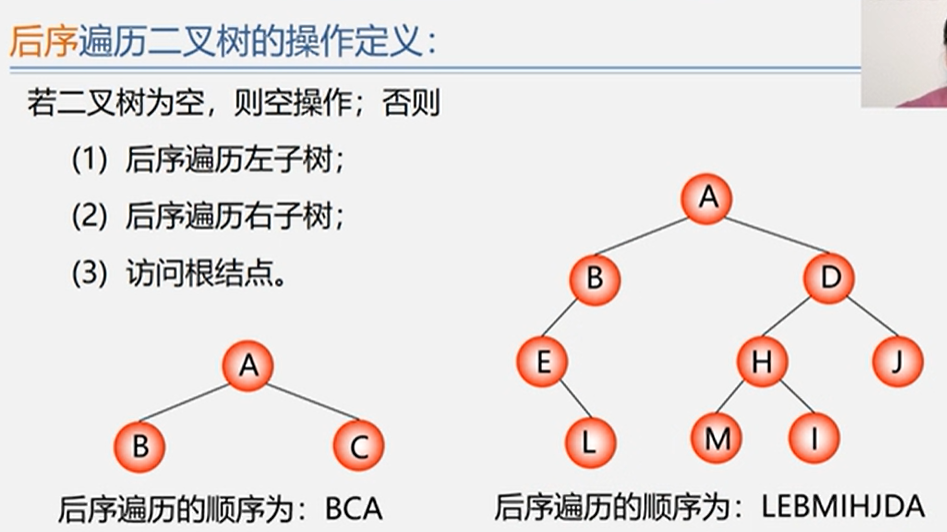
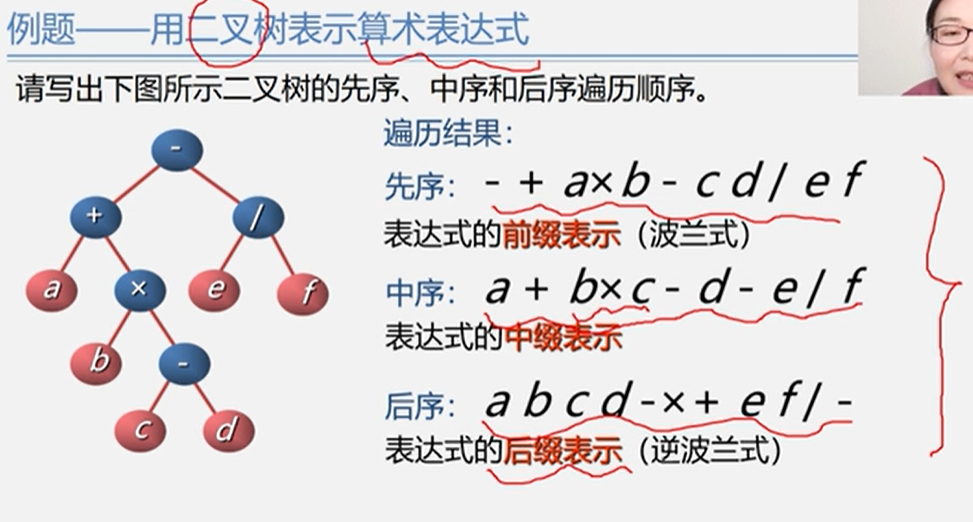
波兰式（先序）、逆波兰式（后序）等：

//定义节点
typedef struct BiNode{
    ElemType data;      //数据域
    struct BiNode *lchild, *rchild;         //左右孩子指针
}BiNode, *BiTree;

//二叉树先序遍历算法 - 根 左 右
int PreOrderTraverse(BiTree T){
    if( T ==   NULL){       //若是空二叉树，则直接返回0
        return 1;
    }else{
        visit(T);       //访问根节点（自定义visit()方法，比如获取该节点的数据域）
        PreOrderTraverse(T->lchild);        //遍历递归左子树
        PreOrderTraverse(T->rchild);        //遍历递归右子树
    }
}

//二叉树中序遍历算法 - 左 根 右
int InOrderTraverse(BiTree T){
    if( T == NULL ){        //若是空二叉树，则直接返回
        return 1;
    }else{
        InOrderTraverse(T->lchild);     //遍历递归左子树
        visit(T);       //访问根节点
        InOrderTraverse(T->rchild);     //遍历递归右子树
    }
}

//二叉树后序遍历算法 - 左 右 根
int PostOrderTraverse(BiTree T){
    if( T == NULL ){
        return 1;
    }else{
        PostOrderTraverse(T->lchild);       //遍历递归左子树
        PostOrderTraverse(T->rchild);       //遍历递归右子树
        visit(T);       //访问根节点
    }
}