【BZOJ2694】Lcm 莫比乌斯反演+线性筛

【BZOJ2694】Lcm

Description

对于任意的>1的n gcd(a, b)不是n^2的倍数
也就是说gcd(a, b)没有一个因子的次数>=2

Input

一个正整数T表示数据组数

接下来T行 每行两个正整数 表示N、M

Output

T行 每行一个整数 表示第i组数据的结果

Sample Input

4
2 4
3 3
6 5
8 3

Sample Output

24
28
233
178

HINT

HINT
T <= 10000

N, M<=4000000

题解：一个数不包含平方因子等价于mu(i)^2=1，所以可以推式子啦：

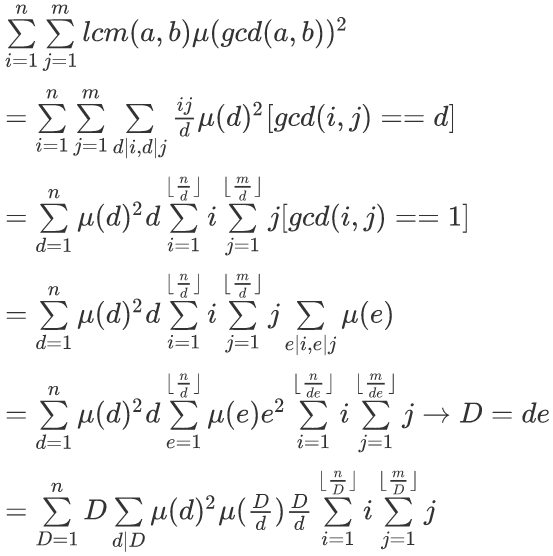
设$f(D)=sumlimits_{d|D}mu(d)^2mu({Dover d}){Dover d}$，然后只要线性筛出f(D)就行了。

还是先考虑D是质数的k次方的情况，若$D=p$，则$f(D)=1 imes 1 imes 1+1 imes (-1) imes p=1-p$；若$D=p^2$，则$f(D)=0+1 imes -1 imes p+0=-p$；若p的次数大于2呢？则$mu(d)$和$mu({Dover d})$中一定有一个等于0，所以f(D)=0。

然后就可以根据积性函数的性质线性筛了。

#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
typedef unsigned int ui;
const ui N=4000000;
ui pri[N/10],np[N+10];
ui f[N+10],s[N+10],sum[N+10],ans,msk;
ui num,T,n,m;
inline ui rd()
{
	ui ret=0;	char gc=getchar();
	while(gc<'0'||gc>'9')	{gc=getchar();}
	while(gc>='0'&&gc<='9')	ret=ret*10+gc-'0',gc=getchar();
	return ret;
}
int main()
{
	ui i,j,p,last;
	f[1]=s[1]=sum[1]=1;
	msk=1,msk<<=30,msk--;
	for(i=2;i<=N;i++)
	{
		if(!np[i])	pri[++num]=i,f[i]=1-i;
		s[i]=s[i-1]+f[i]*i,sum[i]=sum[i-1]+i;
		for(j=1;j<=num&&i*pri[j]<=N;j++)
		{
			p=pri[j],np[i*p]=1;
			if(i%p==0)
			{
				if(i%(p*p)==0)	f[i*p]=0;
				else	f[i*p]=f[i/p]*(-p);
				break;
			}
			f[i*p]=f[i]*(1-p);
		}
	}
	T=rd();
	while(T--)
	{
		n=rd(),m=rd(),ans=0;
		if(n>m)	swap(n,m);
		for(i=1;i<=n;i=last+1)
		{
			last=min(n/(n/i),m/(m/i));
			ans+=(s[last]-s[i-1])*sum[n/i]*sum[m/i];
		}
		printf("%u
",ans&msk);
	}
	return 0;
}