经典的多源最短路径算法——Floyd

　　Floyd算法是经典的求算多源最短路径的算法，它的实质还是一种动态规划思想的应用。

 

一、Floyd算法的实现思想

Floyd算法是如何实现的呢，我下面做简单说明：
　　我们要求算i,j两点间的最短距离，首先我们引入一个中间点k，看看从i到j有没有一条经过k的通路（即i→k→j），如果有这么一条路，那么我们将目前的从i到j的距离，与从i到k再到j的距离相比较，小的那一个更新为新的从i到j的最短路。
那么用dp写出它的状态转移方程有：

　　

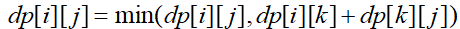
那么在代码里我们要怎样来实现呢？
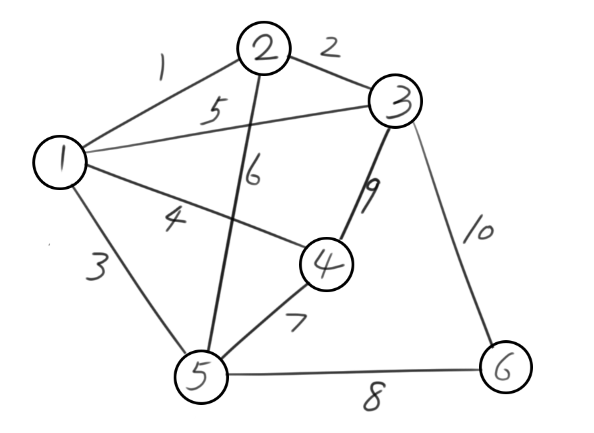
首先需要一个矩阵来储存各个点的关系，对于下面一个图，我们可以得到相应的关系矩阵（数字代表由i到j的路径长度，INF代表目前无法连通）：

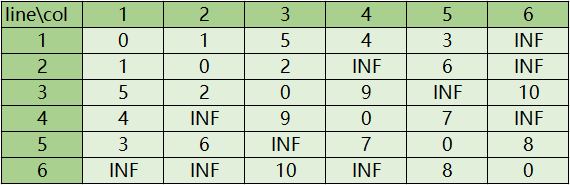
其中第i行第j列就代表从点i到点j的距离。
然后我们需要三层循环，最外层k遍历中间点，里面为i，j遍历矩阵，结合状态转移方程得到Floyd算法的核心代码：

void floyd()
{
    int i,j,k;
    for(k=1;k<=n;k++)
        for(i=1;i<=n;i++)
            for(j=1;j<=n;j++)
            {
                if(dp[i][j]>dp[i][k]+dp[k][j])
                    dp[i][j]=dp[i][k]+dp[k][j];
            }
}

显然我们可以从代码里看出，该算法的时间复杂度为O()。

下面我们用上面的例子来模拟一下。
首先令k=1，开始遍历i，j，对于第(i,j)个关系来说，我们要把它本身的值和第i行第k个、第j列第k个的值的和相比较，取小的作为新的值。如下图

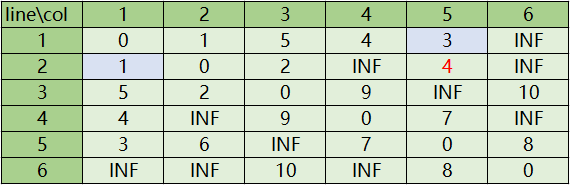
对于第2行第5列的值来说，它的新的值是第2行第1个值和第5列第1个值的和。按照同样的方法我们把k=1的遍历走完

然后我们令k=2再开始遍历

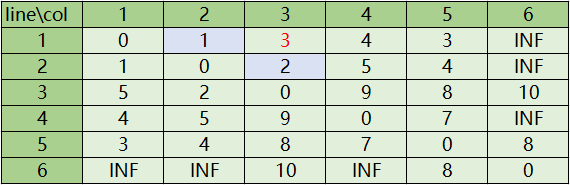
同理，对于第1行第3列的值来说，它的新的值是第1行第2个值和第3列第2个值的和。然后我们把k=2的情况遍历完

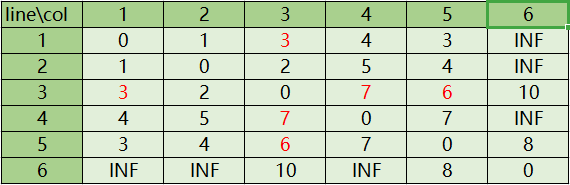
然后我们接着把k=3,4,5…全部遍历完，得到我们的最短路的矩阵

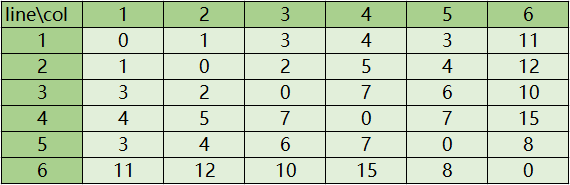
Floyd算法可以求解大多数情况，但是注意Floyd算法无法求解有负权回路的状况，如

对于这个回路来说，它每进行一次循环，最短路就会减少1，所以永远也找不到最短路。

 

二、Floyd算法的正确性

（施工中orz）

 

三、Floyd算法的其他应用

 

1.求解传递闭包

将Floyd算法稍作修改便可以得到求解传递闭包的代码：

void floyd()
{
    int i,j,k;
    for(k=1;k<=n;k++) 
        for(i=1;i<=n;i++)
            for(j=1;j<=n;j++)
                if(matrix[i][k]&&matrix[k][j])
                    matrix[i][j]=1;
}

若有会Warshall算法求传递闭包的朋友便会发现Floyd算法和Warshall算法高度相似！

相关题目：ZOJ P4124

代码：

#include <bits/stdc++.h>

using namespace std;

int n,m,matrix[105][105],num[2][105],flag=0;

void floyd()
{
    int i,j,k;

    for(k=1;k<=n;k++)      //floyd
        for(i=1;i<=n;i++)
            for(j=1;j<=n;j++)
                if(matrix[i][k]&&matrix[k][j])
                    matrix[i][j]=1;

    for(i=1;i<=n;i++)      //判断是否有自环
        for(j=1;j<=n;j++)
            if(matrix[i][j]&&matrix[j][i])
            {
                flag=1;
                return;
            }

    for(i=1;i<=n;i++)    //维护更新num数组
        for(j=1;j<=n;j++)
            if(matrix[i][j])
            {
                num[0][i]++;
                num[1][j]++;
            }
}

int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        int i,a,b;

        memset(matrix,0,sizeof(matrix));    //初始化
        memset(num,0,sizeof(num));
        flag=0;

        scanf("%d%d",&n,&m);
        for(i=0;i<m;i++)    //预处理
        {
            scanf("%d%d",&a,&b);
            matrix[a][b]=1;
        }
        floyd();
        if(flag==0)    //输出，当一个数比它大的和比它小的都小于n/2时，可视为该项为中间项
        {
            for(i=1;i<=n;i++)
            {
                if(num[0][i]<=n/2&&num[1][i]<=n/2) printf("1");
                else printf("0");
            }
            printf("
");
        }
        else
        {
            for(i=0;i<n;i++) printf("0");
            printf("
");
        }
    }
    return 0;
}

（用Floyd算法解此题算是一个比较巧妙的解法）

四、相关题目

1.例题 Luogu P2910

代码：

#include <bits/stdc++.h>

using namespace std;

int matrix[105][105],n;

void floyd()
{
    int i,j,k;
    for(k=1;k<=n;k++)
        for(i=1;i<=n;i++)
            for(j=1;j<=n;j++)
            {
                matrix[i][j]=min(matrix[i][j],matrix[i][k]+matrix[k][j]);
            }
}


int main()
{
    int i,j,m,order[10005]={0},ans=0;
    scanf("%d%d",&n,&m);
    for(i=0;i<m;i++) scanf("%d",&order[i]);
    for(i=1;i<=n;i++)
        for(j=1;j<=n;j++) scanf("%d",&matrix[i][j]);
    floyd();
    for(i=0;i<m-1;i++)
        ans+=matrix[order[i]][order[i+1]];
    printf("%d",ans);
    return 0;
}

Author : Houge　　Date : 2019.6.1

Update log :