小小c#算法题

树型结构是一类重要的非线性数据结构，树是以分支关系定义的层次结构，是n（n>=0)个结点的有限集。关于树的基本概念不再作过多陈述，相信大家都有了解，如有遗忘，可翻书或去其他网页浏览以温习。  

树中结点的最大层次数称为树的深度（Depth）或高度。 

 

本文中以二叉树为例来讲述求树的深度的算法。  

 

在算法开始之前，我们要有数据，即一棵树，树又是结点的集合。所以，应该先定义结点的数据结构（结点的基本属性和操作），然后再定义树的数据结构（树的基本属性和操作）。本文的重点不是讲如何去创建树的数据结构，所以一切从简，本文只是简单构造了结点的数据结构，创建一些结点，然后把这些结点按照逻辑关系关联起来，组成一棵树。而并没有专门去构造树的数据结构，如果要构造树的数据结构，应该有添加结点(InsertChild)的方法，求树的深度也应该作为树的一个方法存在。  

下面是结点的类的定义：

　　class Node
    {
        public int Value
        {
            get;
            set;
        }

        public Node LeftChild
        {
            get;
            set;
        }

        public Node RightChild
        {
            get;
            set;
        }
    }

 
接下来我们就可以定义一系列的结点，设置左右孩子结点形成分支结构的一棵树。下面是Main方法中的代码：

static void Main(string[] args)
        {
            // 创建结点，并通过设置左右孩子组成一棵树
            Node root = new Node() { Value = 1 };
            Node level21 = new Node() { Value = 2 };
            Node level22 = new Node() { Value = 3 };
            Node level31 = new Node() { Value = 4 };
            Node level32 = new Node() { Value = 5 };
            Node level33 = new Node() { Value = 6 };
            Node level41 = new Node() { Value = 7 };

            root.LeftChild = level21;
            root.RightChild = level22;
            level21.LeftChild = level31;
            level22.LeftChild = level32;
            level22.RightChild = level33;
            level32.RightChild = level41;

            // 求树的深度 
            //int treeDepth = GetTreeDepth(root); //递归求解
            int treeDepth = GetTreeDepthByLoop(root); //非递归求解
            Console.WriteLine(treeDepth);
            Console.ReadKey();
        }

 

通过以上代码，我们构成了如下的一棵树： 

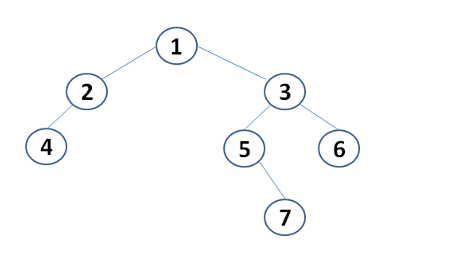
可以看出，这棵树的深度是4。下面就来讨论求树的深度的算法。 

 

1.递归求解： 

采用递归可以把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解。拿上面生成的树来说，如果要求其深度，那么只要取其左子树（以2为根结点的子树）和右子树（以3为根结点的子树）深度的最大值，然后加1即可。由此递归处理下去，直到一棵树只有一个根结点的时候，可知其深度为1，这里是递归的边界条件，这时可以返回上一层的递归。  

下面是代码：

private static int GetTreeDepth(Node root)
        {
            if (root == null)
            {
                return 0;
            }
            else
            {
                int leftTreeDepth = GetTreeDepth(root.LeftChild);
                int rightTreeDepth = GetTreeDepth(root.RightChild);

                if (leftTreeDepth >= rightTreeDepth)
                {
                    return leftTreeDepth + 1;
                }
                else
                {
                    return rightTreeDepth + 1;
                }
            }
        }

想不通的同学可以拿上面创建好的树来手动地走一遍。 

 

2.直接求解： 

直接求解的思想也十分简单，我们可以称之为广度优先遍历。从根结点开始，得到其所有孩子结点，放到一个集合A中，这个集合A中即第二层（根结点为第一层）的所有结点。如果这个集合A不为空，说明其深度至少为2，这时，我们把记录树的深度的变量加1，由初始的1变为2。然后我们遍历这个集合A中的所有结点，即遍历树的第二层的结点，同时把第二层中所有结点的子结点放到另外一个集合B中，这样，另外一个集合B中存放的就是第三层的结点。如果集合B不为空，那么记录深度的变量再加1。这时清空集合A，准备存放下一层的结点，如此循环下去，其间集合A,B交替使用，一个用来存放正在遍历的结点，一个存放下一次要遍历的孩子结点，直到当某一层的结点数为0时，说明已经到树的最底层，可以退出循环了，记录深度的变量此时的值就是树的深度。 

 

代码如下： 

// 循环实现，广度优先遍历
        private static int GetTreeDepthByLoop(Node root)
        {
            if (root == null) return 0;

            int depth = 1;
            List<Node> nodes1 = new List<Node>();
            List<Node> nodes2 = new List<Node>();
            List<Node> temp;

            nodes1.Add(root);

            while (true)
            {
                foreach (Node n in nodes1)
                {
                    if (n.LeftChild != null)
                    {
                        nodes2.Add(n.LeftChild);
                    }

                    if (n.RightChild != null)
                    {
                        nodes2.Add(n.RightChild);
                    }
                }

                if (nodes2.Count > 0) depth++;
                else return depth;

                nodes1.Clear();
                temp = nodes1;
                nodes1 = nodes2;
                nodes2 = temp;
            }
        }
    }

 

关于main方法中调用上述两种方法的代码，在给出创建树的代码时已经一并给出。