【20171005】Luogu P2752 [USACO4.3]街道赛跑Street Race——BFS的基础应用

Luogu P2752 [USACO4.3]街道赛跑Street Race

题目描述

图一表示一次街道赛跑的跑道。可以看出有一些路口（用 0 到 N 的整数标号），和连接这些路口的箭头。路口 0 是跑道的起点，路口 N 是跑道的终点。箭头表示单行道。运动员们可以顺着街道从一个路口移动到另一个路口（只能按照箭头所指的方向）。当运动员处于路口位置时，他可以选择任意一条由这个路口引出的街道。

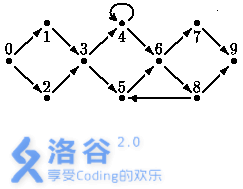
图一：有 10 个路口的街道

一个良好的跑道具有如下几个特点：

每一个路口都可以由起点到达。

从任意一个路口都可以到达终点。

终点不通往任何路口。

运动员不必经过所有的路口来完成比赛。有些路口却是选择任意一条路线都必须到达的（称为“不可避免”的）。在上面的例子中，这些路口是 0，3，6，9。对于给出的良好的跑道，你的程序要确定“不可避免”的路口的集合，不包括起点和终点。

假设比赛要分两天进行。为了达到这个目的，原来的跑道必须分为两个跑道，每天使用一个跑道。第一天，起点为路口 0，终点为一个“中间路口”；第二天，起点是那个中间路口，而终点为路口 N。对于给出的良好的跑道，你的程序要确定“中间路口”的集合。如果良好的跑道 C 可以被路口 S 分成两部分，这两部分都是良好的，并且 S 不同于起点也不同于终点，同时被分割的两个部分满足下列条件：（1）它们之间没有共同的街道（2）S 为它们唯一的公共点，并且 S 作为其中一个的终点和另外一个的起点。那么我们称 S 为“中间路口 ”。在例子中只有路口 3 是中间路口。

输入输出格式

输入格式：

输入文件包括一个良好的跑道，最多有 50 个路口，100 条单行道。

一共有 N+2 行，前面 N+1 行中第 i 行表示以编号为(i-1)的路口作为起点的街道，每个数字表示一个终点。行末用 -2 作为结束。最后一行只有一个数字 -1。

输出格式：

第一行包括：跑道中“不可避免的”路口的数量，接着是这些路口的序号，序号按照升序排列。

第二行包括：跑道中“中间路口”的数量，接着是这些路口的序号，序号按照升序排列。

输入输出样例

输入样例#1：

1 2 -2
3 -2
3 -2
5 4 -2
6 4 -2
6 -2
7 8 -2
9 -2
5 9 -2
-2
-1

输出样例#1：

2 3 6
1 3

说明

题目翻译来自NOCOW。

USACO Training Section 4.3

代码：

//Concerned WebSite: https://www.luogu.org/problem/show?pid=2752
#include<stdio.h>
#include<math.h>
#define MAXN 51
int g[MAXN][MAXN]={0};//1==has street
int g_temp[MAXN][MAXN]={0};//1==has street
int n_node;
int avoidAble[MAXN]={0};//1==is AvoidAble; 0==unAvoidAble or unknown;
int divideAble[MAXN]={0};//1==is DivideAble; 0==unDivideAble or unknown;
int reachedNode[MAXN]={0};//the node we have reached in this BFS
//=============顽皮的分割线==============================================================
void myReadin()
{
    int count=0;
    int temp;
    scanf("%d",&temp);
    while(temp!=-1)
    {
        while(temp!=-2)
        {
            g[count][temp]=1;
            scanf("%d",&temp);
        }
        count++;
        scanf("%d",&temp);
    }
    n_node=count;
    return ;
}
//=============顽皮的分割线============================================================== 
int checkIsAvoidAble(int node)//1==is AvoidAble; 0==is unavoidAble
{
    //-----BFS-------
    
    int line[MAXN]={0};
    int top,bot;
    int i;
    int ans=0;//ready to return .
    top=0;bot=1;
    line[top]=0;
    
    for(i=0;i<n_node;i++)    reachedNode[i]=0;
    
    while(bot>top)
    {
        reachedNode[line[top]]=1;//do a sign
        if(line[top]==n_node-1)//reach the end
            ans=1;
        for(i=0;i<n_node;i++)//==========i<n_node?=========================
        {
            if(g_temp[line[top]][i]==1&&reachedNode[i]==0)//it has a new destination
            {
                line[bot++]=i;
                reachedNode[i]=1;
                if(i==n_node-1)//reached the end
                    ans=1;
                    //why we do not stop this function immediately?
                    //Because we need "reachedNode[]" in next function.
            }
        }
        top++;
    } 
    return ans;
}
//=============顽皮的分割线==============================================================
int checkIsDivideAble(int node)//1==is DivideAble; 0==is unDivideAble
{
    int i;
    for(i=0;i<n_node;i++)//==========i=0? i<n_node?=========================
    {
        if(g[node][i]==1&&reachedNode[i]==1)//can run from start to node's nearest destinations
            return 0;
    }
    int j;
    for(i=0;i<n_node-1;i++)
    {
        if(reachedNode[i]==1)
            for(j=i+1;j<n_node;j++)
            {
                if(reachedNode[j]==0&&j!=node)
                    if(g[i][j]==1||g[j][i]==1)//there is a street between 2 sets
                        return 0;
            }
    }
    return 1;
}
//=============顽皮的分割线==============================================================
void copyG(int deleteNode)
{
    int i,j;
    for(i=0;i<n_node;i++)
    {
        for(j=0;j<n_node;j++)
        {
            g_temp[i][j]=g[i][j];
            if(i==deleteNode||j==deleteNode||i==j)
                g_temp[i][j]=0;
        }
    }
    return ;
}
//=============顽皮的分割线==============================================================
int main()
{
    myReadin();
    
    //find "the points that cannot be avoided"
    int i;
    for(i=1;i<n_node-1;i++)//==========i<n_node-1?=========================
    {
        copyG(i);
        if(checkIsAvoidAble(i)==0)//unAvoidAble
        {
            avoidAble[i]=0;
            if(checkIsDivideAble(i)==1)//DivideAble
            {
                divideAble[i]=1;
            }
        }
        else
            avoidAble[i]=1;
        
    }
    
    int avcount=0;
    for(i=1;i<n_node-1;i++)
        if(avoidAble[i]==0)
            avcount++;
    printf("%d ",avcount);
    
    for(i=1;i<n_node-1;i++)
        if(avoidAble[i]==0)
            printf("%d ",i);
    printf("
");
    
    avcount=0;
    for(i=1;i<n_node;i++)
        if(divideAble[i]==1)
            avcount++;
    printf("%d ",avcount);
    
    for(i=1;i<n_node;i++)
        if(divideAble[i]==1)
            printf("%d ",i);
    printf("
");
    
    return 0;
}
//=============顽皮的分割线==============================================================

代码真的是我自己写的，看英文注释的语法那么蹩脚就知道了~~~啊啊啊啊~~~详细的解释会在之后更新唔……