二叉树先序、中序、后序遍历的递归算法和非递归算法

先序遍历：若二叉树为空，则空操作；否则访问根节点；先序遍历左子树；先序遍历右子树。

中序遍历：若二叉树为空，则空操作；否则中序遍历左子树；访问根节点；中序遍历右子树。

后序遍历：若二叉树为空，则空操作；否则后序遍历左子树；后序遍历右子树；访问根节点。

二叉链表：链表中的结点包含三个域：数据域和左右指针域。

三叉链表：在二叉链表的基础上增加指向双亲结点的指针域。

以下代码均使用二叉链表。

//二叉树的二叉链表存储表示
typedef char TElemType;
typedef struct BiNode
{
	TElemType data;
	struct BiNode *lchild, *rchild;
} BiNode , *BiTree;

1.      生成二叉树

可以在遍历过程中生成结点，建立二叉树的存储结构。按先序序列建立二叉树的二叉链表的算法如下：

/* 
 * 按先序次序输入二叉树中结点的值(一个字符)，空格字符表示空树，构造二叉链表表示的二叉树T。
 */
Status CreatBiTree(BiTree *T)
{
	char ch;
	scanf("%c", &ch);

	//如果当前输入的字符为空格，则(*T)指向空树。
	if (ch == ' ')
	{
		(*T) = NULL;
	}
	else
	{
		if (!((*T) = (BiTree)malloc(sizeof(BiNode))))
			exit(OVERFLOW);
		(*T)->data = ch;				//生成根结点
		CreatBiTree(&((*T)->lchild));	//构造左子树
		CreatBiTree(&((*T)->rchild));	//构造右子树
	}
	return OK;
}

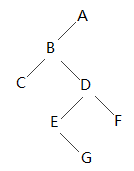
假设输入字符依次为ABC##DE#G##F###(#表示空格)，则生成的二叉树如下所示：

2.      二叉树遍历递归算法

a.       先序遍历

/*
 * 采用二叉链表存储结构，Visit是对数据元素操作的应用函数，
 * 先序遍历二叉树T的递归算法，对每个数据元素调用函数Visit。
 */
Status PreOrderTraverse_Recursive(BiTree T, Status(*Visit)(TElemType e))
{
	if (T)
	{
		if (Visit(T->data))
			if (PreOrderTraverse_Recursive(T->lchild, Visit))
				if (PreOrderTraverse_Recursive(T->rchild, Visit))
					return OK;
		return ERROR;	//函数不会执行到这一步，不会返回Error。这样写只是为了没有编译警告。
	}
	else
		return OK;	//当T为空树时，停止递归。
}

b.      中序遍历

Status InOrderTraverse_Recursive(BiTree T, Status(*Visit)(TElemType e))
{
	if (T)
	{
		if (InOrderTraverse_Recursive(T->lchild, Visit))
			if (Visit(T->data))
				if (InOrderTraverse_Recursive(T->rchild, Visit))
					return OK;
		return ERROR;
	}
	else
		return OK;
}

c.       后序遍历

Status PostOrderTraverse_Recursive(BiTree T, Status(*Visit)(TElemType e))
{
	if (T)
	{
		if (PostOrderTraverse_Recursive(T->lchild, Visit))
			if (PostOrderTraverse_Recursive(T->rchild, Visit))
				if (Visit(T->data))
					return OK;
		return ERROR;
	}
	else
		return OK;
}

3.      二叉树遍历非递归算法

a.       先序遍历

/*
 * 先序遍历二叉树，非递归算法。
 */
Status PreOrderTraverse_NonRecursive(BiTree T, Status(*Visit)(TElemType e))
{
	Stack *S;	//栈S中存储指向树结点的指针。
	BiTree p;
	S = (Stack*)malloc(sizeof(Stack));
	InitStack(S);
	Push(S, T);	//根指针进栈。
	while (!StackEmpty(S))
	{
		//获取栈顶指针，如果栈顶指针不为空，访问该结点。并将该结点的左子树进栈。
		if (GetTop(S, &p) && p)
		{
			if (!Visit(p->data))
				return ERROR;
			Push(S, p->lchild);
		}
		//栈顶指针为空，表明之前压入的左子树或者右子树为空。
		else
		{
			Pop(S, &p);	//空指针退栈
			if (!StackEmpty(S))
			{
				Pop(S, &p); //已被访问过的根结点退栈。此时，该退栈结点的左子树已被全部访问过。
				Push(S, p->rchild);	//右子树进栈。
			}
		}
	}
	return OK;
}

b.      中序遍历

/* 
 * 采用二叉链表存储结构，Visit是对数据元素进行操作的应用函数，
 * 中序遍历二叉树的非递归算法，对每个数据元素调用函数Visit。
 */
Status InOrderTraverse_NonRecursive(BiTree T, Status(*Visit)(TElemType e))
{
	Stack *S;
	BiTree p;
	S = (Stack *)malloc(sizeof(Stack));
	InitStack(S);
	Push(S, T);	//根指针进栈
	while (!StackEmpty(S))
	{
		//向左走到尽头
		while (GetTop(S, &p) && p)
		{
			Push(S, p->lchild);
		}

		//空指针退栈
		Pop(S, &p);

		//访问节点，并向右一步
		if (!StackEmpty(S))
		{
			Pop(S, &p);
			if (!Visit(p->data))
				return ERROR;
			Push(S, p->rchild);
		}
	}
	return OK;
}

或者

/*
 * 采用二叉链表存储结构，Visit是对数据元素进行操作的应用函数，
 * 中序遍历二叉树的非递归算法，对每个数据元素调用函数Visit。
 */
Status InOrderTraverse_NonRecursive_2(BiTree T, Status(*Visit)(TElemType e))
{
	Stack *S;
	BiTree p = T;
	S = (Stack *)malloc(sizeof(Stack));
	InitStack(S);

	while (p || !StackEmpty(S))
	{
		//根指针进栈，遍历左子树
		if (p)
		{
			Push(S, p);
			p = p->lchild;
		}
		//根指针退栈，访问根结点，遍历右子树
		else
		{
			Pop(S, &p);
			if (!Visit(p->data))
				return ERROR;
			p = p->rchild;
		}
	}
	return OK;
}

c.       后序遍历

/*
 * 后序遍历二叉树，非递归算法
 */
Status PostOrderTraverse_NonRecursive(BiTree T, Status(*Visit)(TElemType e))
{
	Stack *S;
	BiTree p, pre=NULL;//pre指向已访问过的最后一个结点。
	S = (Stack*)malloc(sizeof(Stack));
	InitStack(S);
	Push(S, T);//根指针进栈

	while (!StackEmpty(S))
	{
		//获取栈顶指针，如果当前结点有左子树，并且左子树结点不是刚被访问的节点。如果当前结点有右子树，并且右子树结点不是刚被访问的结点。
		//表明栈顶指针指向的树结点未被访问，且左子树和右子树均未被访问。此时，将结点的左子树进栈。
		if (GetTop(S, &p) && p->lchild && pre != p->lchild && !(p->rchild && pre == p->rchild))
			Push(S, p->lchild);
		//如果栈顶指针的右子树存在，且未被访问。则将右子树进栈
		else if (p->rchild && pre != p->rchild)
			Push(S, p->rchild);
		//如果左子树和右子树均被访问过，则结点退栈，并进行访问。更新pre。
		else
		{
			Pop(S, &p);
			if (!Visit(p->data))
				return ERROR;
			pre = p;
		}
	}
	return OK;
}

4.测试完整代码

/*
 * 假设输入字符为：ABC##DE#G##F###，实际输入时，#用空格代替。
 */
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <malloc.h>
#include <stdlib.h>

typedef int Status;
#define OK 1
#define ERROR 0
#define OVERFLOW -2

//二叉树的二叉链表存储表示
typedef char TElemType;
typedef struct BiNode
{
	TElemType data;
	struct BiNode *lchild, *rchild;
} BiNode , *BiTree;

//栈的顺序存储结构
#define STACK_INIT_SIZE 100      //存储空间初始分配量
#define STACKINCREMENT 10       //存储空间分配增量

typedef struct
{
	BiTree *base;
	BiTree *top;
	int stacksize;
} Stack;

//函数声明
Status InitStack(Stack *S);
Status Push(Stack *S, BiTree p);
Status Pop(Stack *S, BiTree *p);
Status GetTop(Stack *S, BiTree *p);
Status StackEmpty(Stack *S);

Status CreatBiTree(BiTree *T);
Status PreOrderTraverse_Recursive(BiTree T, Status(*Visit)(TElemType e));
Status InOrderTraverse_Recursive(BiTree T, Status(*Visit)(TElemType e));
Status PostOrderTraverse_Recursive(BiTree T, Status(*Visit)(TElemType e));
Status PreOrderTraverse_NonRecursive(BiTree T, Status(*Visit)(TElemType e));
Status InOrderTraverse_NonRecursive(BiTree T, Status(*Visit)(TElemType e));
Status InOrderTraverse_NonRecursive_2(BiTree T, Status(*Visit)(TElemType e));
Status PostOrderTraverse_NonRecursive(BiTree T, Status(*Visit)(TElemType e));

Status PrintElement(TElemType e);

int main()
{
	BiTree T;
	CreatBiTree(&T);
	//先序
	PreOrderTraverse_Recursive(T, PrintElement); putchar('
');
	PreOrderTraverse_NonRecursive(T, PrintElement); putchar('
');
	//中序
	InOrderTraverse_Recursive(T, PrintElement); putchar('
');
	InOrderTraverse_NonRecursive(T, PrintElement); putchar('
');
	InOrderTraverse_NonRecursive_2(T, PrintElement); putchar('
');
	//后序
	PostOrderTraverse_Recursive(T, PrintElement); putchar('
');
	PostOrderTraverse_NonRecursive(T, PrintElement); putchar('
');
	return 0;
}

/* 
 * 按先序次序输入二叉树中结点的值(一个字符)，空格字符表示空树，构造二叉链表表示的二叉树T。
 */
Status CreatBiTree(BiTree *T)
{
	char ch;
	scanf("%c", &ch);

	//如果当前输入的字符为空格，则(*T)指向空树。
	if (ch == ' ')
	{
		(*T) = NULL;
	}
	else
	{
		if (!((*T) = (BiTree)malloc(sizeof(BiNode))))
			exit(OVERFLOW);
		(*T)->data = ch;				//生成根结点
		CreatBiTree(&((*T)->lchild));	//构造左子树
		CreatBiTree(&((*T)->rchild));	//构造右子树
	}
	return OK;
}

/*
 * 采用二叉链表存储结构，Visit是对数据元素操作的应用函数，
 * 先序遍历二叉树T的递归算法，对每个数据元素调用函数Visit。
 */
Status PreOrderTraverse_Recursive(BiTree T, Status(*Visit)(TElemType e))
{
	if (T)
	{
		if (Visit(T->data))
			if (PreOrderTraverse_Recursive(T->lchild, Visit))
				if (PreOrderTraverse_Recursive(T->rchild, Visit))
					return OK;
		return ERROR;	//函数不会执行到这一步，不会返回Error。这样写只是为了没有编译警告。
	}
	else
		return OK;	//当T为空树时，停止递归。
}

Status InOrderTraverse_Recursive(BiTree T, Status(*Visit)(TElemType e))
{
	if (T)
	{
		if (InOrderTraverse_Recursive(T->lchild, Visit))
			if (Visit(T->data))
				if (InOrderTraverse_Recursive(T->rchild, Visit))
					return OK;
		return ERROR;
	}
	else
		return OK;
}

Status PostOrderTraverse_Recursive(BiTree T, Status(*Visit)(TElemType e))
{
	if (T)
	{
		if (PostOrderTraverse_Recursive(T->lchild, Visit))
			if (PostOrderTraverse_Recursive(T->rchild, Visit))
				if (Visit(T->data))
					return OK;
		return ERROR;
	}
	else
		return OK;
}

/*
 * 先序遍历二叉树，非递归算法。
 */
Status PreOrderTraverse_NonRecursive(BiTree T, Status(*Visit)(TElemType e))
{
	Stack *S;	//栈S中存储指向树结点的指针。
	BiTree p;
	S = (Stack*)malloc(sizeof(Stack));
	InitStack(S);
	Push(S, T);	//根指针进栈。
	while (!StackEmpty(S))
	{
		//获取栈顶指针，如果栈顶指针不为空，访问该结点。并将该结点的左子树进栈。
		if (GetTop(S, &p) && p)
		{
			if (!Visit(p->data))
				return ERROR;
			Push(S, p->lchild);
		}
		//栈顶指针为空，表明之前压入的左子树或者右子树为空。
		else
		{
			Pop(S, &p);	//空指针退栈
			if (!StackEmpty(S))
			{
				Pop(S, &p); //已被访问过的根结点退栈。此时，该退栈结点的左子树已被全部访问过。
				Push(S, p->rchild);	//右子树进栈。
			}
		}
	}
	return OK;
}

/* 
 * 采用二叉链表存储结构，Visit是对数据元素进行操作的应用函数，
 * 中序遍历二叉树的非递归算法，对每个数据元素调用函数Visit。
 */
Status InOrderTraverse_NonRecursive(BiTree T, Status(*Visit)(TElemType e))
{
	Stack *S;
	BiTree p;
	S = (Stack *)malloc(sizeof(Stack));
	InitStack(S);
	Push(S, T);	//根指针进栈
	while (!StackEmpty(S))
	{
		//向左走到尽头
		while (GetTop(S, &p) && p)
		{
			Push(S, p->lchild);
		}

		//空指针退栈
		Pop(S, &p);

		//访问节点，并向右一步
		if (!StackEmpty(S))
		{
			Pop(S, &p);
			if (!Visit(p->data))
				return ERROR;
			Push(S, p->rchild);
		}
	}
	return OK;
}

/*
 * 采用二叉链表存储结构，Visit是对数据元素进行操作的应用函数，
 * 中序遍历二叉树的非递归算法，对每个数据元素调用函数Visit。
 */
Status InOrderTraverse_NonRecursive_2(BiTree T, Status(*Visit)(TElemType e))
{
	Stack *S;
	BiTree p = T;
	S = (Stack *)malloc(sizeof(Stack));
	InitStack(S);

	while (p || !StackEmpty(S))
	{
		//根指针进栈，遍历左子树
		if (p)
		{
			Push(S, p);
			p = p->lchild;
		}
		//根指针退栈，访问根结点，遍历右子树
		else
		{
			Pop(S, &p);
			if (!Visit(p->data))
				return ERROR;
			p = p->rchild;
		}
	}
	return OK;
}

/*
 * 后序遍历二叉树，非递归算法
 */
Status PostOrderTraverse_NonRecursive(BiTree T, Status(*Visit)(TElemType e))
{
	Stack *S;
	BiTree p, pre=NULL;//pre指向已访问过的最后一个结点。
	S = (Stack*)malloc(sizeof(Stack));
	InitStack(S);
	Push(S, T);//根指针进栈

	while (!StackEmpty(S))
	{
		//获取栈顶指针，如果当前结点有左子树，并且左子树结点不是刚被访问的节点。如果当前结点有右子树，并且右子树结点不是刚被访问的结点。
		//表明栈顶指针指向的树结点未被访问，且左子树和右子树均未被访问。此时，将结点的左子树进栈。
		if (GetTop(S, &p) && p->lchild && pre != p->lchild && !(p->rchild && pre == p->rchild))
			Push(S, p->lchild);
		//如果栈顶指针的右子树存在，且未被访问。则将右子树进栈
		else if (p->rchild && pre != p->rchild)
			Push(S, p->rchild);
		//如果左子树和右子树均被访问过，则结点退栈，并进行访问。更新pre。
		else
		{
			Pop(S, &p);
			if (!Visit(p->data))
				return ERROR;
			pre = p;
		}
	}
	return OK;
}

//遍历数据元素时所调用函数
Status PrintElement(TElemType e)
{
	putchar(e);
	return OK;
}

//初始化栈
Status InitStack(Stack *s)
{
	s->base = (BiTree*)malloc(sizeof(BiTree)*STACK_INIT_SIZE);
	s->top = s->base;
	s->stacksize = STACK_INIT_SIZE;
	return OK;
}

//获得栈顶元素
Status GetTop(Stack *s, BiTree *c)
{
	if (StackEmpty(s))
		return ERROR;
	*c = *(s->top - 1);
	return OK;
}

//判断栈是否为空
Status StackEmpty(Stack *s)
{
	if (s->base == s->top)
		return OK;
	return ERROR;
}

//进栈
Status Push(Stack *s, BiTree c)
{
	//如果空间不够，增加空间的分配
	if (s->top - s->base >= s->stacksize)
	{
		s->base = (BiTree*)realloc(s->base, sizeof(BiTree)*(s->stacksize + STACKINCREMENT));
		s->stacksize = s->stacksize + STACKINCREMENT;
	}

	*(s->top++) = c;
	return OK;
}

//出栈
Status Pop(Stack *s, BiTree *c)
{
	if (StackEmpty(s))
		return ERROR;
	*c = *(--s->top);
	return OK;
}

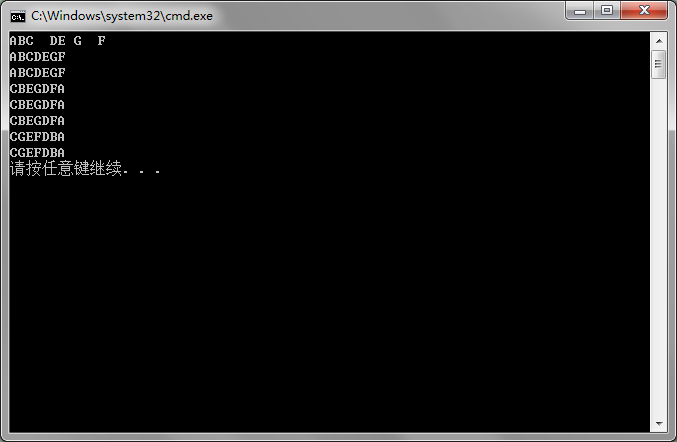
5.测试结果

注：程序中生成的树为上图中的树