1. 堆
堆:n个元素序列{k1,k2,...,ki,...,kn},当且仅当满足下列关系时称之为堆:
(ki <= k2i,ki <= k2i+1)
或者(ki >= k2i,ki >= k2i+1), (i = 1,2,3,4,...,n/2)
若将和此次序列对应的一维数组(即以一维数组作此序列的存储结构)看成是一个完全二叉树,则堆的含义表明,完全二叉树中所有非终端结点的值均不大于(或不小于)其左、右孩子结点的值。由此,若序列{k1,k2,…,kn}是堆,则堆顶元素(或完全二叉树的根)必为序列中n个元素的最小值(或最大值)。
一般用数组来表示堆,i结点的父结点下标就为(i–1)/2。它的左右子结点下标分别为2*i+1和2*i+2。如第0个结点的左右子结点下标分别为1和2。
2. 堆的插入
每次插入都是将先将新数据放在数组最后,由于从这个新数据的父结点到根结点必然为一个有序的序列,现在的任务是将这个新数据插入到这个有序序列中——这就类似于直接插入排序中将一个数据并入到有序区间中。
代码:
/*
* 堆插入算法。(小顶堆)
* 先将num插入堆尾,易知从新数据的父结点到根结点是一个有序的序列,
* 将num插入到该有序序列当中,该过程为直接插入排序。
* 未插入前数据长度为n。
*/
int HeapInsert(int *heap, int n, int num)
{
int i, j;
heap[n] = num;//num插入堆尾
i = n;
j = (n - 1) / 2;//j指向i的父结点
//注意不要漏掉i!=0的条件。因为必须保证i有父结点j。j>=0并不能保证i!=0。
//如果没有此条件,当i=0时,j=0,若heap[0]>num,程序就会陷入死循环。
while (j >= 0 && i != 0)
{
if (heap[j] <= num)
break;
heap[i] = heap[j];
i = j;
j = (i - 1) / 2;
}
heap[i] = num;
return 0;
}
3. 堆的删除
堆中每次都只能删除堆顶元素。为了便于重建堆,实际的操作是将最后一个数据的值赋给根结点,然后再从根结点开始进行一次从上向下的调整。调整时先在左右子结点中找最小的,如果父结点比这个最小的子结点还小说明不需要调整了,反之将父结点和它交换后再考虑后面的结点。相当于根结点数据的“下沉”过程。
代码:
/*
* 堆删除算法。(删除堆顶元素)
* n表示未删除前堆中数据的总数。
*/
int HeapDelete(int *heap, int n)
{
//使用堆尾元素直接覆盖堆顶元素。
heap[0] = heap[n - 1];
//从堆顶到堆尾(此时堆中只有n-1个元素)进行堆调整。
HeapAdjust(heap, 0, n - 1);
return 0;
}
/*
* 堆调整算法。(小顶堆)
* 已知heap[top]结点的左右子树均为堆,调整堆中元素,使以heap[top]为根结点的树为堆。
* n为堆中元素总数。
*/
int HeapAdjust(int *heap, int top, int n)
{
int j = 2 * top + 1; //左孩子结点
int temp = heap[top];
while (j < n)
{
if (j + 1 < n&&heap[j + 1] < heap[j])
j++; //使j指向左右孩子中较小的结点。
if (heap[j] >= temp)
break;
heap[top] = heap[j];
top = j;
j = 2 * top + 1;
}
heap[top] = temp;
return 0;
}
4. 堆的建立
从无序序列建堆的过程就是一个反复调整的过程。若将此序列看成是一个完全二叉树,则最后一个非终端结点是第(n-2)/2个结点,由此调整过程只需从该结点开始,直到堆顶元素。
代码:
/*
* 建堆算法。
* 将无序数组array[]转换为堆。
*/
int CreatHeap(int *array, int n)
{
int i;
//最后一个结点的编号为n-1,该结点的父节点(n-2)/2为最后一个非终端结点。
//从结点(n-2)/2到根结点,依次进行堆调整。
for (i = (n - 2) / 2; i >= 0; i--)
{
HeapAdjust(array, i, n);
}
return 0;
}
5. 堆排序
若在输出堆顶的最小值之后,使得剩余n-1个元素的序列重建一个堆,则得到n个元素中的次小值。如此反复执行,便能得到一个有序序列,这个过程称之为堆排序。
输出堆顶元素之后,以堆中最后一个元素替代之,此时根结点的左右子树均为堆,则仅需进行一次从上到下的调整即可重建一个堆。
代码:
/*
* 堆排序算法。
* 形参heap为大顶堆时,实现的是由小到大;
* 形参heap为小顶堆时,实现的是由大到小;
*/
int HeapSort(int *heap, int n)
{
int i;
int temp;
for (i = n - 1; i > 0; i--)
{
//将堆顶元素和未排序的最后一个元素交换。
temp = heap[0];
heap[0] = heap[i];
heap[i] = temp;
//交换之后进行堆调整
HeapAdjust(heap, 0, i);
}
return 0;
}
6. 测试代码
/*
* 堆的建立、插入、删除和堆排序算法
*/
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#define TOTAL 20
int HeapInsert(int *heap, int n, int num);
int HeapDelete(int *heap, int n);
int HeapAdjust(int *heap, int top, int n);
int HeapSort(int *heap, int n);
int CreatHeap(int *array, int n);
int main()
{
int heap[TOTAL];
int num;
int i;
//先输入一半的数据,对输入的数组建堆。
printf("输入Total/2个数据:
");
for (i = 0; i < TOTAL / 2; i++)
scanf("%d", &heap[i]);
CreatHeap(heap, TOTAL / 2);
//检验是否建堆成功。
printf("建堆后:
");
for (i = 0; i < TOTAL / 2; i++)
printf("%-3d", heap[i]);
putchar('
');
//向已建好的堆中插入数据,并重组为堆。
printf("继续输入Total/4个数据:
");
for (i = TOTAL / 2; i < TOTAL / 2 + TOTAL / 4; i++)
{
scanf("%d", &num);
HeapInsert(heap, i, num);
}
//检验是否插入成功。
printf("重组为堆之后:
");
for (i = 0; i < TOTAL / 2 + TOTAL / 4; i++)
printf("%-3d", heap[i]);
putchar('
');
//删除堆顶元素Total/4次。
printf("删除Total/4个数据:
");
for (i = 0; i < TOTAL / 4; i++)
HeapDelete(heap, TOTAL / 2 + TOTAL / 4 - i);
//检验是否删除成功。
for (i = 0; i < TOTAL / 2; i++)
printf("%-3d", heap[i]);
putchar('
');
//向堆中插满数据,进行堆排序。
printf("继续输入Total/2个数据:
");
for (i = TOTAL / 2; i < TOTAL; i++)
{
scanf("%d", &num);
HeapInsert(heap, i, num);
}
HeapSort(heap, TOTAL);
printf("排序后:
");
for (i = 0; i < TOTAL; i++)
printf("%-3d ", heap[i]);
putchar('
');
return 0;
}
/*
* 堆插入算法。(小顶堆)
* 先将num插入堆尾,易知从新数据的父结点到根结点是一个有序的序列,
* 将num插入到该有序序列当中,该过程为直接插入排序。
* 未插入前数据长度为n。
*/
int HeapInsert(int *heap, int n, int num)
{
int i, j;
heap[n] = num;//num插入堆尾
i = n;
j = (n - 1) / 2;//j指向i的父结点
//注意不要漏掉i!=0的条件。因为必须保证i有父结点j。j>=0并不能保证i!=0。
//如果没有此条件,当i=0时,j=0,若heap[0]>num,程序就会陷入死循环。
while (j >= 0 && i != 0)
{
if (heap[j] <= num)
break;
heap[i] = heap[j];
i = j;
j = (i - 1) / 2;
}
heap[i] = num;
return 0;
}
/*
* 堆删除算法。(删除堆顶元素)
* n表示未删除前堆中数据的总数。
*/
int HeapDelete(int *heap, int n)
{
//使用堆尾元素直接覆盖堆顶元素。
heap[0] = heap[n - 1];
//从堆顶到堆尾(此时堆中只有n-1个元素)进行堆调整。
HeapAdjust(heap, 0, n - 1);
return 0;
}
/*
* 堆调整算法。(小顶堆)
* 已知heap[top]结点的左右子树均为堆,调整堆中元素,使以heap[top]为根结点的树为堆。
* n为堆中元素总数。
*/
int HeapAdjust(int *heap, int top, int n)
{
int j = 2 * top + 1; //左孩子结点
int temp = heap[top];
while (j < n)
{
if (j + 1 < n&&heap[j + 1] < heap[j])
j++; //使j指向左右孩子中较小的结点。
if (heap[j] >= temp)
break;
heap[top] = heap[j];
top = j;
j = 2 * top + 1;
}
heap[top] = temp;
return 0;
}
/*
* 堆排序算法。
* 形参heap为大顶堆时,实现的是由小到大;
* 形参heap为小顶堆时,实现的是由大到小;
*/
int HeapSort(int *heap, int n)
{
int i;
int temp;
for (i = n - 1; i > 0; i--)
{
//将堆顶元素和未排序的最后一个元素交换。
temp = heap[0];
heap[0] = heap[i];
heap[i] = temp;
//交换之后进行堆调整
HeapAdjust(heap, 0, i);
}
return 0;
}
/*
* 建堆算法。
* 将无序数组array[]转换为堆。
*/
int CreatHeap(int *array, int n)
{
int i;
//最后一个结点的编号为n-1,该结点的父节点(n-2)/2为最后一个非终端结点。
//从结点(n-2)/2到根结点,依次进行堆调整。
for (i = (n - 2) / 2; i >= 0; i--)
{
HeapAdjust(array, i, n);
}
return 0;
}
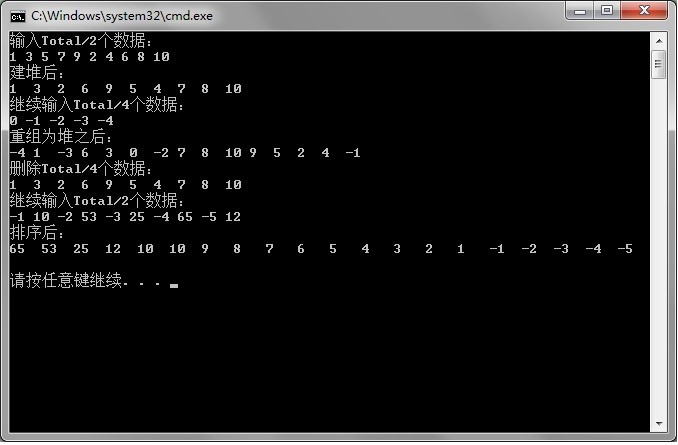
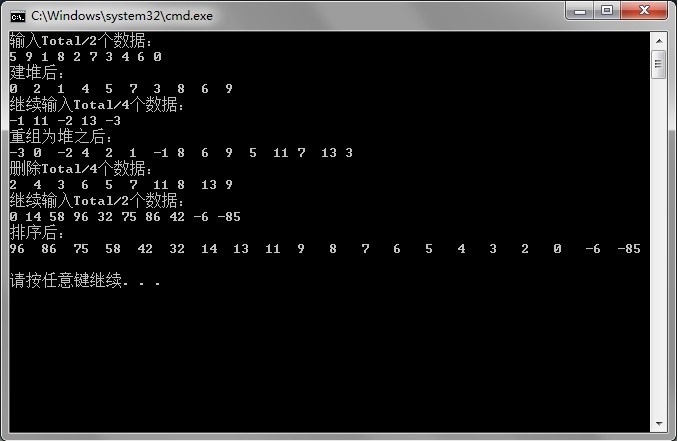
7. 测试结果