题目链接
https://codeforces.com/contest/1439/problem/B

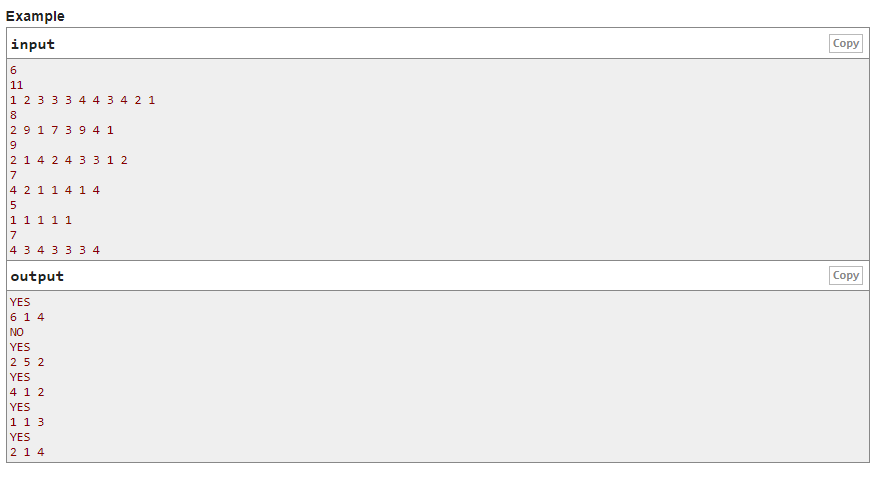
题意
给你一个有(n)个顶点和(m)条边的无向图,和一个整数(k)。
请你找到(k)个点使得他们俩俩之间互相有连边, 或一个非空的顶点子集,使该子集的每个顶点在该子集中至少有(k)个邻居。
思路
首先 一个点的度数小于 $k - 1 $ 那么他对俩种方案都没有贡献,可以从图中删去它以及它所连的边。
考虑类似拓扑排序, 每次把度数小于(k)的点以及所连的边删除, 如果最后还有点剩余,那么就是方案2.
对于方案一,我们可以在删除度数为(k - 1)的点时候暴力枚举这个点和其所链接的(k - 1)个点能不能组成方案一。
暴力枚举我们可以用对边排序二分检查边是否存在,复杂度(O(k^2log m))。
当((k - 1) * k / 2 > m) 的时候无解。
AC代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 2e5 + 50;
vector<int> G[maxn];
int du[maxn];
int vis[maxn];
int main()
{
std::ios::sync_with_stdio(false);
int t;
cin >> t;
while(t--){
int n, m, k;
cin >> n >> m >> k;
for(int i = 1;i <= n;i++) G[i].clear(), vis[i] = 0, du[i] = 0;
for(int i = 0;i < m;i++){
int u, v;
cin >> u >> v;
G[u].push_back(v);
G[v].push_back(u);
du[u]++, du[v]++;
}
for(int i = 1;i <= n;i++) sort(G[i].begin(), G[i].end());
queue<int> q;
vector<int> ans1, ans2;
for(int i = 1;i <= n;i++){
if(du[i] < k){
q.push(i);
vis[i] = 1;
}
}
if(1LL * k * (k - 1) / 2 > m){
cout << -1 << endl;
continue;
}
while(!q.empty()){
int u = q.front(); q.pop();
vis[u] = 2;
if(du[u] == k - 1 && ans2.empty()){
ans2.push_back(u);
for(auto v : G[u]) if(vis[v] <= 1) ans2.push_back(v);
int ok = 1;
for(auto i : ans2){
for(auto j : ans2){
if(i == j) break;
if(!binary_search(G[i].begin(), G[i].end(), j)) ok = 0;
}
if(!ok) ans2.clear();
}
}
for(auto v : G[u]){
du[v]--;
if(du[v] < k && !vis[v]){
q.push(v);
vis[v] = 1;
}
}
}
for(int i = 1;i <= n;i++) if(!vis[i]) ans1.push_back(i);
if(ans1.size() > 0){
cout << 1 << " " << ans1.size() << endl;
for(auto i : ans1) cout << i << " ";cout << endl;
}
else if(ans2.size() > 0){
cout << 2 << endl;
for(auto i : ans2) cout << i << " ";cout << endl;
}
else cout << -1 << endl;
}
return 0;
}