前言:一道标签很多很毒瘤但思路非常连贯的图论背景/算法运用杂题。
题目描述
小周猪猪手里拿到一个地图,地图显示的是一个n个点和m条边的连通的有向无环图。
现在小周猪猪需要寻找一条路径,使得这条路径是可爱路径且可爱路径的可爱度最大。
一条路径是可爱路径当且仅当可以从路径的一端走到路径的另一端,且路径经过的边数一定要大于或等于k。且路径上的每一个节点只能够经过一次。
在这里,可爱值定义为:一串n个在可爱路径上的点的点权形成一个升序序列后第int(n/2.0) + 1个数。
现在,小周猪猪想知道可爱路径的最大可爱值,请你输出这个最大可爱值。
如果地图中不存在可爱路径输出,则输出No
输入格式
第一行:三个数,分别是n, m和 k 。表示点的个数,边的条数以及可爱路径经过边数的约束条件。
第二行:共有n个数,第i个数表示节点i的点权。
接下来m行:每行两个数x和y,表示x到y有一条有向边。
输出格式
所有可爱路径中的最大可爱值。
样例输入1:
7 8 3
46 79 97 33 22 1 122
1 2
1 5
2 3
2 6
3 4
6 4
5 7
4 7
样例输出1:
97
样例输入2:
7 8 8
46 79 97 33 22 1 122
1 2
1 5
2 3
2 6
3 4
6 4
5 7
4 7
样例输出2:
No

分析
看到最大值,直接联想到二分答案即要求的最大可爱值。最大可爱值保证在 -1e9 到 1e9 之间,显然具有单调性。
那么考虑二分中check函数的写法。
如果按照以往的思路,判断每一个 (mid) 是否可行比较的难实现。于是我们可以换一种方式,在每一次 (check) 的时候判断是否有比 (mid) 更优的解,如果有就加大 (mid) 的值,反之减小即可。
显然,一个数列 (A) 如果枚举到任意一个 (mid) 比它大的数的个数比比它小的数的个数大,则 (A) 的中位数一定大于等于 (mid)。比它大的数的个数比比它小的数的个数小,则 (A) 的中位数一定小于等于 (mid)。(取等条件需判断数列长度的奇偶)
于是我们可以定义一个 (v_f) 数组。如果当前点权大于等于 (mid) 那么 (v_f[i] = 1),否则 (v_f[i] = -1)。
那么对于一段点的点权权,我们将它们对应的 (v_f) 数组求和,如果这个和大于0,则这一段点的中位数一定大于 (mid),即存在比 (mid) 更优的解,返回 true,否则返回 false。
这就相当于需要把一张图拉成链,直接拓扑排序求出拓扑序进行操作即可。
而判断函数的内部我们用dp来实现。定义 (dp[i][j]) 表示到达 (i)点,且长度为 (j) 的路径的最大 (v_f) 和。如果你发现有一个 (j >= k)(满足可爱路径) 且 (dp[i][j] >= 0) (存在更优的解)那么直接返回 true。
(dp) 的遍历直接将拓扑序里的点顺次拉出,在拓展节点即可。由此不难推出状态转移方程,部分代码如下:
for(int i = 1; i <= n; i++)
for(int j = 0; j <= n; j++)
dp[i][j] = -INF;
for(int i = 1; i <= n; i++) {
int x = Topo_num[i]; // 拓扑序。
dp[x][0] = v_f[x];
// 初始化。(长度为0,到x的路径经过的点显然只有x一个点故最大直接是x的点权。
for(int j = 0; j <= n; j++) { // 枚举长度
if(dp[x][j] >= 0 && j >= k)
return true; // 判断是否有可爱路径上的最优解
for(int k = 0; k < map[x].size(); k++) {
// 拓展
int y = map[x][k];
dp[y][j + 1] = max(dp[y][j + 1], dp[x][j] + v_f[y]); // 更新
// dp[x][j] 表示到 x 且长度为 j 的路径,加上一个 v_f[j] 显然就是到 y 且长度为 j + 1 的路径
}
}
}
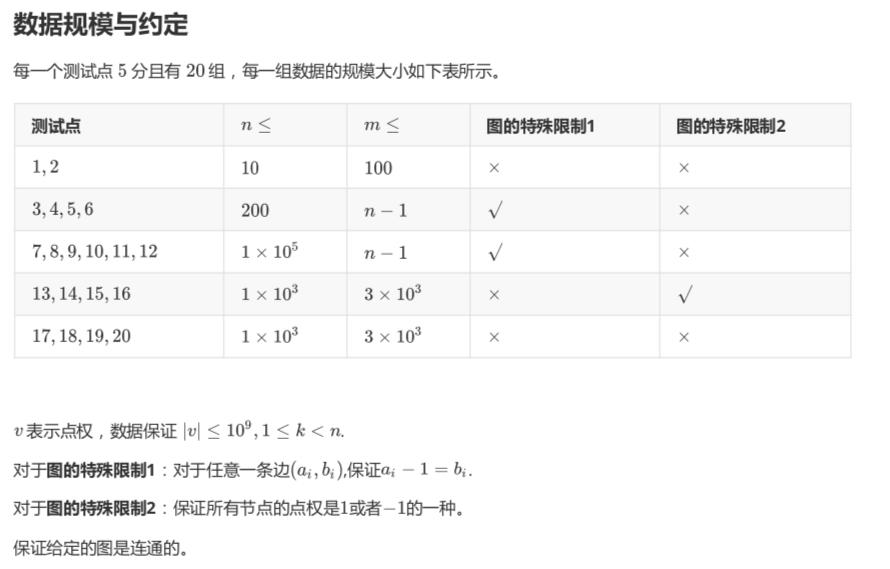
但这道题还没完。因为数据非常的毒瘤,当 (n <= 1e5) 的时候没法开 (dp) 二维数组,不过好在这时候的图题目说满足限制一,即是一条单链。
真.面向数据编程
那么在这种情况下,我们只需要改写一下 (check) 函数就可以了。
是一个单链的话,(check) 就可以改写为求长度大于等于 (k) 的所有子串中元素总和最大的子串。前缀和乱搞即可。
for(int i = 1; i <= n; i++) {
sum[i] = sum[i - 1] + v_f[i]; // 前缀和
ma[i] = min(ma[i - 1], sum[i]);
// 求出之前的最小值,因为我们不强制长度,所以可以只考虑如何满足最大(显然就是当前元素前缀和-k个元素之前最小的前缀和)
}
int t;
for(int i = k + 1; i <= n; i++) {
int j = i - k;
// 保证是可爱路径,并找到满足可爱路径的情况下前面最小的前缀和。
t = sum[i] - ma[j];
if(t >= 0) // 代表有更优解
return true;
}
AC代码
#include <cstdio>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;
const int MAXN = 3005;
const int MAXM = 1e5 + 5;
const int INF = 0x3f3f3f3f;
void read(int &x) {
x = 0;
int k = 1;
char s = getchar();
while(s < '0' || s > '9') {
if(s == '-')
k = -1;
s = getchar();
}
while(s >= '0' && s <= '9') {
x = (x << 1) + (x << 3) + (s ^ 48);
s = getchar();
}
x *= k;
return ;
}
int n, m, k;
int in[MAXM], v[MAXM], v_f[MAXM];
vector<int> map[MAXM];
void Add_Edge(int u, int v) {
map[u].push_back(v);
return ;
}
int Topo_num[MAXM];
int Topo_len = 0;
void Topo_Sort() {
// 拓扑排序
queue<int> q;
for(int i = 1; i <= n; i++)
if(!in[i])
q.push(i);
while(!q.empty()) {
int now = q.front();
q.pop();
Topo_len++;
Topo_num[Topo_len] = now;
for(int i = 0; i < map[now].size(); i++) {
int v = map[now][i];
in[v]--;
if(!in[v])
q.push(v);
}
}
}
int dp[MAXN][MAXN];
bool check2(int mid) { // 无限制条件的 check 函数
for(int i = 1; i <= n; i++)
if(v[i] >= mid)
v_f[i] = 1;
else
v_f[i] = -1;
for(int i = 1; i <= n; i++)
for(int j = 0; j <= n; j++)
dp[i][j] = -INF;
for(int i = 1; i <= n; i++) {
int x = Topo_num[i]; // 拓扑序。
dp[x][0] = v_f[x];
// 初始化。(长度为0,到x的路径经过的点显然只有x一个点故最大直接是x的点权。
for(int j = 0; j <= n; j++) { // 枚举长度
if(dp[x][j] >= 0 && j >= k)
return true; // 判断是否有可爱路径上的最优解
for(int k = 0; k < map[x].size(); k++) {
// 拓展
int y = map[x][k];
dp[y][j + 1] = max(dp[y][j + 1], dp[x][j] + v_f[y]); // 更新
}
}
}
return false;
}
int sum[MAXM], ma[MAXM];
bool check(int mid) { // 单链的check函数
ma[0] = INF;
for(int i = 1; i <= n; i++) {
if(v[i] >= mid)
v_f[i] = 1;
else
v_f[i] = -1;
sum[i] = sum[i - 1] + v_f[i];
ma[i] = min(ma[i - 1], sum[i]);
// 求出之前的最小值,因为我们不强制长度,所以可以只考虑如何满足最大(显然就是当前元素前缀和-k个元素之前最小的前缀和)
}
int t;
for(int i = k + 1; i <= n; i++) {
int j = i - k;
// 保证是可爱路径,并找到满足可爱路径的情况下前面最小的前缀和。
t = sum[i] - ma[j];
if(t >= 0) // 代表有更优解
return true;
}
}
int main() {
read(n); read(m); read(k);
for(int i = 1; i <= n; i++)
read(v[i]);
bool flag = false;
for(int i = 1; i <= m; i++) {
int x, y;
read(x); read(y);
Add_Edge(x, y);
in[y]++;
if(x - 1 != y) // 判断当前图是否满足限制一
flag = true;
}
if(!flag) { // 单链
int l = -1e9, r = 1e9, ans = 0;
while(l <= r) {
int mid = (l + r) >> 1;
if(check(mid)) {
l = mid + 1;
ans = mid;
}
else r = mid - 1;
}
if(ans == 0)
printf("No");
else
printf("%d", ans);
}
else { // 无限制条件
Topo_Sort();
// for(int i = 1; i <= n; i++)
// printf("%d
", Topo_num[i]);
int l = -1e9, r = 1e9, ans = 0;
while(l <= r) {
int mid = (l + r) >> 1;
if(check2(mid)) {
l = mid + 1;
ans = mid;
}
else r = mid - 1;
}
if(ans == 0)
printf("No");
else
printf("%d", ans);
}
return 0;
}
这道题其实思维难度还挺高的,(check) 函数很难往是否存在最优解这个方向去想。
注:涵妹发现二分还可以在优化一下,没必要从 -1e9 到 1e9,因为最后的答案一定是在 (v) 数组里的,所以我们可以建一个 (v2) 数组,在一开始把 (v) 数组的值赋到 (v2) 里,然后对 (v2) 排序,二分直接在 (v2) 数组里做即可(这时二分里的 (l, r) 表示 (v2) 的下标)