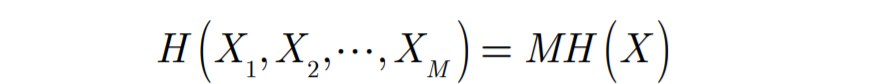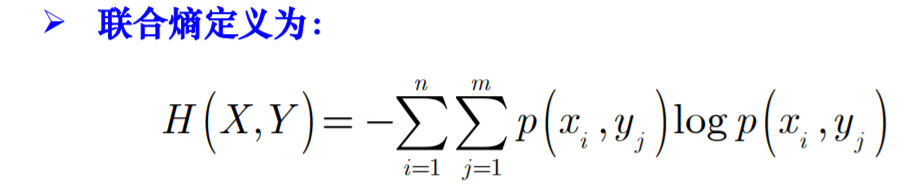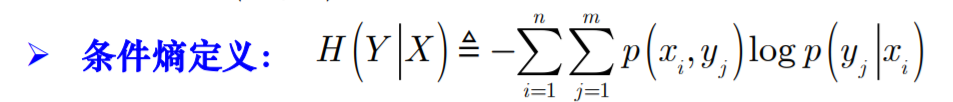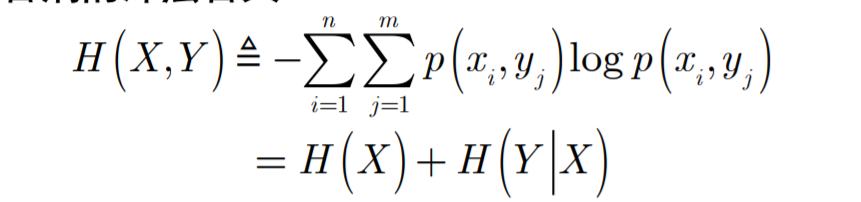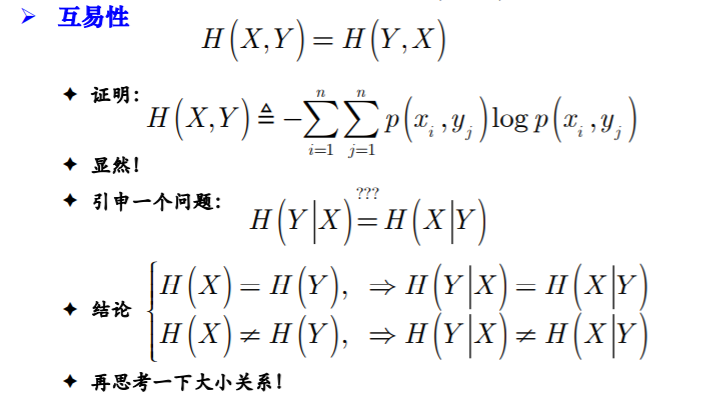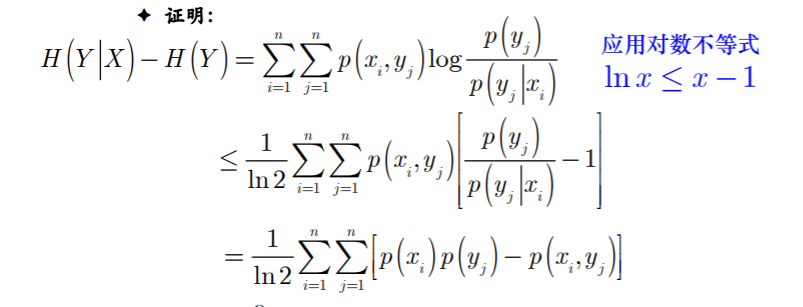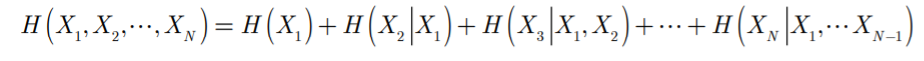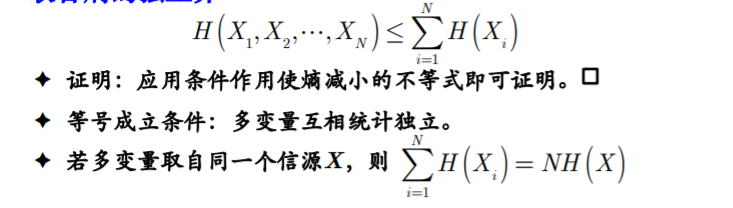- 幕布链接【查看更方便】:第二讲
- 第二讲:离散信源及其信息熵
- 自信息量
- 自信息量定义
- 见图

- 见图
- 自信息量计算
- 见图

- 见图
- 总结
-
- 自信息量定义
- 单符号离散信源信息熵
- 历史:
-
- 定义:
-
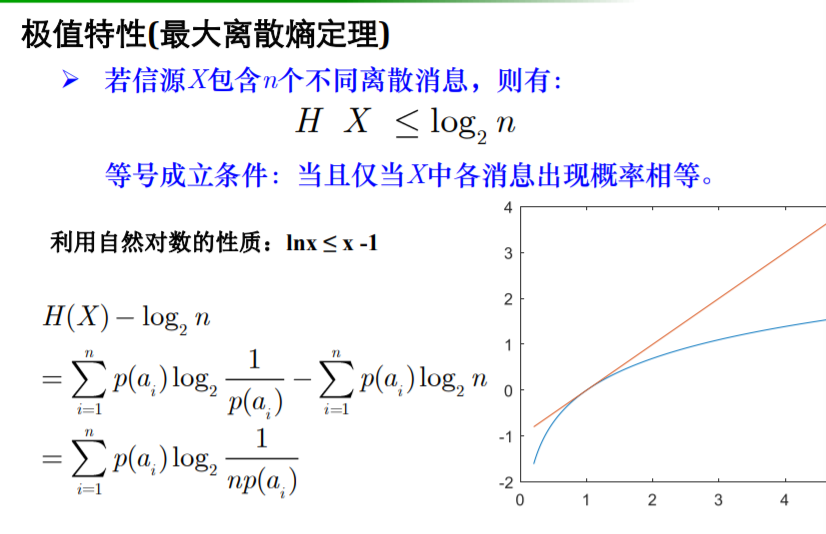
- 最大离散熵定理:
- 定理

- 证明:

- 二元信号的信息熵【和深度学习中的交叉 熵一样-】

- 定理
- 总结:
- 总结:

- 总结:
- 历史:
- 多符号离散信源信息熵
- 两符号独立同分布情况——多符号独立同分布
- 熵模型
- 熵模型

- 熵模型
- 利用独立性计算结果:
-
- M个独立同分布
-
- 熵模型
- 联合熵
- 定义:
-
- 利用条件概率公式——联合熵计算
-
- 条件熵:
-
- 联合熵计算结果:
-
- 联合熵的深层含义【结合熵表示信源的不确定度来理解】
-
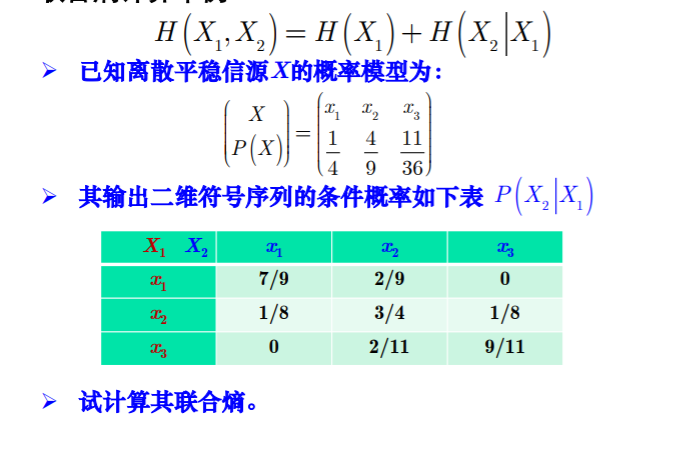
- 例题一道:
-
- 性质:
- 互易性
-
- 条件作用使熵减小
-
- N个信源联合熵链式法则
-
- 独立界:
-
- 互易性
- 扩展练习【以信源去考虑】
- 01


- 思考4解答:利用定义去思考参考证明一【证明过程待补充】
- 01
- 定义:
- 两符号独立同分布情况——多符号独立同分布
- 上面总结【忙的话可以直接看这儿】
- 熵公式
-
- 联合熵性质:
-
- 熵公式
- 离散平稳信源
- 平稳概念:
- 图示
- 一种简单的离散平稳信源【马尔可夫信源】
- 状态:
- 图示:

- 图示:
- 转移概率:
- 图示

- 图示
- 举例说明上述属性
- 图示【思考数字电路中的状态转移】
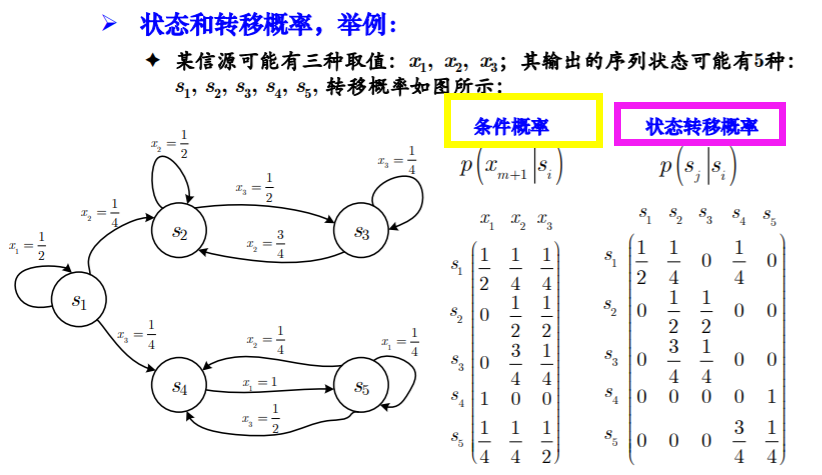
- 图示【思考数字电路中的状态转移】
- 熵
- 证明:极限熵 = 条件熵
- 图示


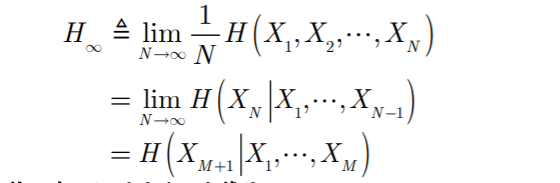
- 图示
- 一阶马尔可夫熵的特性【注意物理意义】
- 图示

- 一阶特性是什么??【未解答】
- 图示
- 极限熵计算公式【思考用矩阵计算】
- 图示:【注意时不变的理解】

- 图示:【注意时不变的理解】
- 一个例子:【补充matlab代码】未完成
- 图示

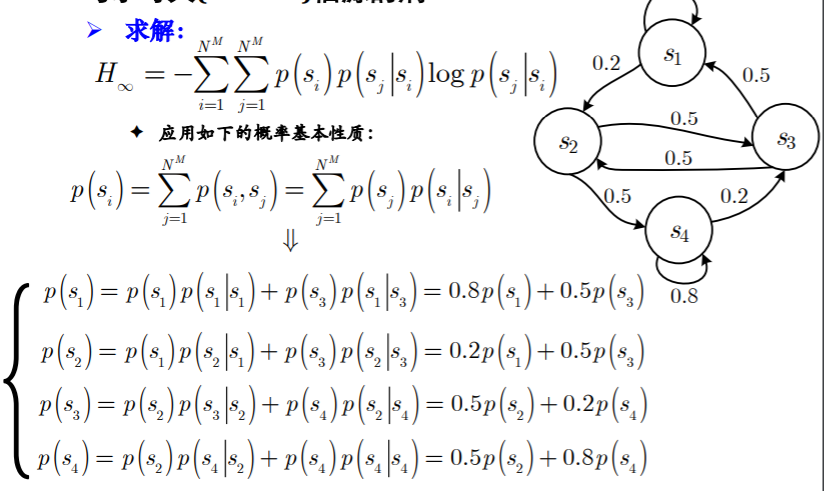
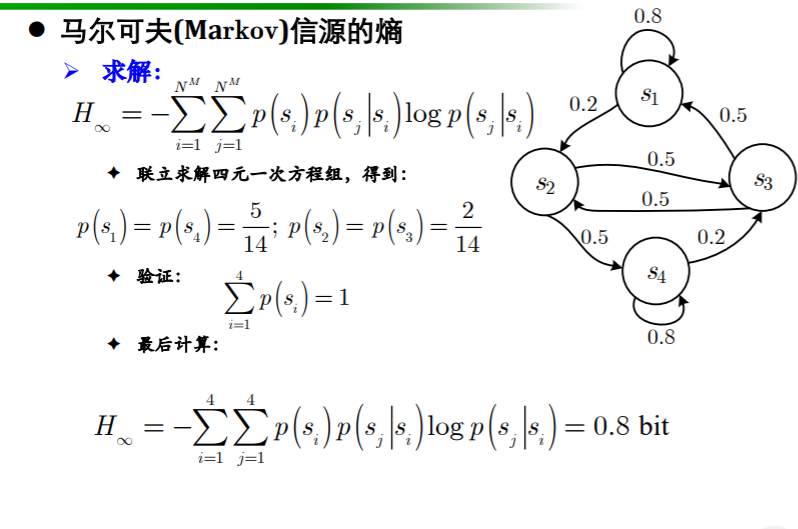
- 图示
- 上一道题的matlab代码
- 证明:极限熵 = 条件熵
- 状态:
- 平稳概念:
- 本讲全部总结:
- 信息的基本度量
- 图示

- 图示
- 重要特性
- 图示

- 图示
- 思考如何用matlab实现熵求解过程【矩阵思想】
- 信息的基本度量
- 例题练手
- 01:抛硬币
- 图示

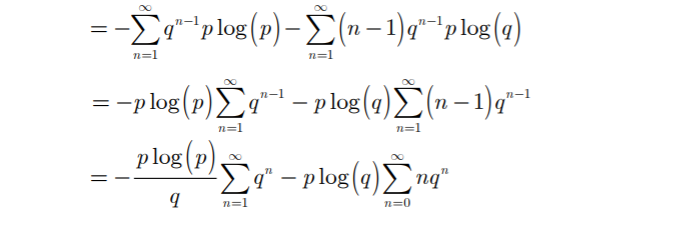
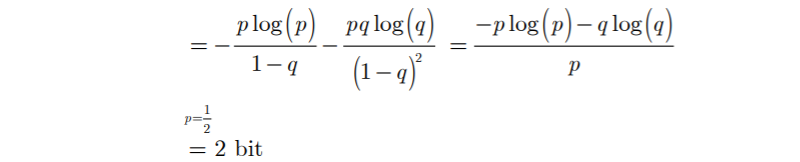
- 图示
- 02:随机变量函数的熵
- 图示:

- 图示:
- 03:扑克洗牌过程使熵增加 【思考】
- 图示

- 图示
- 04: 小狗寻觅骨头的极限熵【思考】
- 图示


- 图示
- 01:抛硬币
- 自信息量