学习率调度

原文链接：https://d2l.ai/chapter_optimization/lr-scheduler.html

在神经网络中，通常我们主要关注优化算法如何更新权重，而缺少关注更新的幅度，即学习率。适当的调整学习率和优化算法一样重要。可以从这些角度去考虑：

• 【学习率大小】最直观的就是学习率的粒度很重要。如果学习率太大，优化曲线就会发散，如果学习率太小，训练时间会超级长，或者最终得到一个次优结果。
• 【衰减因子】其次，衰减因子也很重要，如果学习率一直保持较大的值，那么最终可能会在最优点附近反复跳动，而无法得到最优解。
• 【预热】另一个重要的方面就是初始化。包括参数如何初始化以及参数初期如何进化。这被称为预热warmup，也就是在训练初始的时候，我们向解决方案前进的速度有多快。开始的时候大步前进可能没有好处，因为初始设置的参数是随机设置的，所以初始的更新方向可能是没有意义的。
• 最后，有很多优化变量都在进行周期性的学习率调整。因此，推荐阅读“Averaging weights leads to wider optima and better generalization”，如何通过在整个参数路径上求平均值来获得更好的解。

基于学习率调整有很多细节，所以很多深度学习框架都有工具来自动处理这件事。

1. 举个例子

下边是使用类似LeNet的结构对Fashion-MNIST数据（一个类似手写体数字识别的图像分类数据集）进行分类。

from d2l import tensorflow as d2l
import tensorflow as tf
import math
from tensorflow.keras.callbacks import LearningRateScheduler

def net():
    return tf.keras.models.Sequential([
        tf.keras.layers.Conv2D(filters=6, kernel_size=5, activation='relu',
                               padding='same'),
        tf.keras.layers.AvgPool2D(pool_size=2, strides=2),
        tf.keras.layers.Conv2D(filters=16, kernel_size=5,
                               activation='relu'),
        tf.keras.layers.AvgPool2D(pool_size=2, strides=2),
        tf.keras.layers.Flatten(),
        tf.keras.layers.Dense(120, activation='relu'),
        tf.keras.layers.Dense(84, activation='sigmoid'),
        tf.keras.layers.Dense(10)])


batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size=batch_size)

# The code is almost identical to `d2l.train_ch6` defined in the
# lenet section of chapter convolutional neural networks
def train(net_fn, train_iter, test_iter, num_epochs, lr,
              device=d2l.try_gpu(), custom_callback = False):
    device_name = device._device_name
    strategy = tf.distribute.OneDeviceStrategy(device_name)
    with strategy.scope():
        optimizer = tf.keras.optimizers.SGD(learning_rate=lr)
        loss = tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True)
        net = net_fn()
        net.compile(optimizer=optimizer, loss=loss, metrics=['accuracy'])
    callback = d2l.TrainCallback(net, train_iter, test_iter, num_epochs,
                             device_name)
    if custom_callback is False:
        net.fit(train_iter, epochs=num_epochs, verbose=0,
                callbacks=[callback])
    else:
         net.fit(train_iter, epochs=num_epochs, verbose=0,
                 callbacks=[callback, custom_callback])
    return net

让我们看一下默认设置情况下，算法的学习情况，比如lr=0.3，iterations=30. 可以注意到，当测试准确率在某一点后就停滞不前了，但是训练准确率还在一直提升。这两个曲线之间的间隙表示模型过拟合了。

lr, num_epochs = 0.3, 30
train(net, train_iter, test_iter, num_epochs, lr)

2. 调度器

一种调整学习率的方法就是每一个step都明确指定learning rate。这个可以通过set_learning_rate方法做到。我们可以再每个epoch或mini-batch之后调小一点。也就是根据优化的进度进行动态调整。

lr = 0.1
dummy_model = tf.keras.models.Sequential([tf.keras.layers.Dense(10)])
dummy_model.compile(tf.keras.optimizers.SGD(learning_rate=lr), loss='mse')
print(f'learning rate is now ,', dummy_model.optimizer.lr.numpy())

更通用的方式是希望定一个调度器。当传入更新的次数，它能返回一个适当的学习率。比如我们可以定一个和t的平方根相关的调度器：

class SquareRootScheduler:
    def __init__(self, lr=0.1):
        self.lr = lr

    def __call__(self, num_update):
        return self.lr * pow(num_update + 1.0, -0.5)

我们来看一下SquareRootScheduler是如何随着epoch变化的。

scheduler = SquareRootScheduler(lr=0.1)
d2l.plot(tf.range(num_epochs), [scheduler(t) for t in range(num_epochs)])

下边让我们看下这个调度器在FashionMNIST数据集上的表现。

train(net, train_iter, test_iter, num_epochs, lr,
      custom_callback=LearningRateScheduler(scheduler))

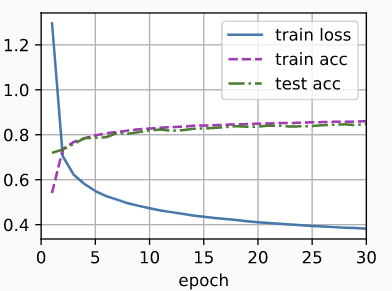
从上图可以看到，这个调度器已经比前边的表现好一些了。可以看出两个现象：

• 和前边的模型相比，这次曲线更加平滑；
• 这次的过拟合得到了缓解；
  不过，这个事实无法很好的回答，为什么某些策略会缓解过拟合。有些观点认为更小的步长导致参数更新幅度接近于0，但是这无法很好的完全解释上述现象，因为我们并没有真的停止，而仅仅是降低了学习率。

常用的调度策略

常规选择是多项式衰减和分段常数调度。此外，cosine学习率调度也被证明在某些任务上表现不错。最后，有些工作适合在使用大的学习率之前，先预热一下。

1. 因子调度器

一种多项式衰减策略就是乘上alpha因子，lr_t+1 = lr_t * alpha, 0 < alpha < 1。为了避免学习率过度衰减，超多一个合理的下界，这个等式通常写作：lr_t+1 = max( lr_t * alpha, lr_min )

class FactorScheduler:
    def __init__(self, factor=1, stop_factor_lr=1e-7, base_lr=0.1):
        self.factor = factor
        self.stop_factor_lr = stop_factor_lr
        self.base_lr = base_lr

    def __call__(self, num_update):
        self.base_lr = max(self.stop_factor_lr, self.base_lr * self.factor)
        return self.base_lr

scheduler = FactorScheduler(factor=0.9, stop_factor_lr=1e-2, base_lr=2.0)
d2l.plot(tf.range(50), [scheduler(t) for t in range(50)])

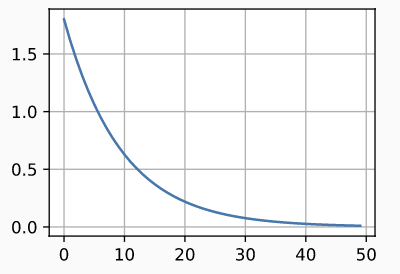
2. 多因子调度器

一个常规的策略是，在训练深度网络时，分阶段保持学习率为一个常量，然后每个阶段都调小一些。也就是说，给定一个时间集合，表示什么时候调小学习率，比如{5，10，20}，也就是当step处于这个集合时，才衰减。比如下边的实现是每次衰减一半。

class MultiFactorScheduler:
    def __init__(self, step, factor, base_lr):
        self.step = step
        self.factor = factor
        self.base_lr = base_lr

    def __call__(self, epoch):
        if epoch in range(self.step[0], (self.step[1] + 1)):
            return self.base_lr * self.factor
        else:
            return self.base_lr

scheduler = MultiFactorScheduler(step=[15, 30], factor=0.5, base_lr=0.5)
d2l.plot(tf.range(num_epochs), [scheduler(t) for t in range(num_epochs)])

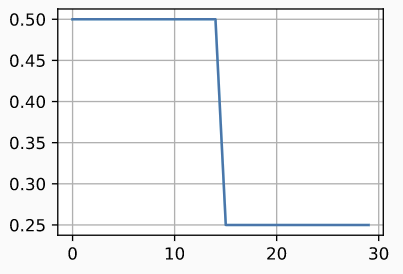
分阶段常数学习率的直觉解释是，每个学习率都可以让优化一直进行到一个权重向量分布比较稳定的状态。然后我们降低学习率，可以得到一个更优的局部最小值。

train(net, train_iter, test_iter, num_epochs, lr,
      custom_callback=LearningRateScheduler(scheduler))

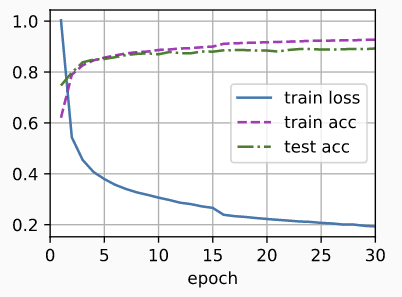
3. Cosine调度器

有人提出了一个相当令人费解的启发式调度方法。它基于这样的观察，我们可能不想在一开始就大幅度的降低学习率，同时，我们又想在最后的时候使用非常小的学习率来改进结果。这就产生了一个类似于余弦的时间表，其学习率的函数形式如下

n_0是初始学习率，n_T是T时刻学习率，对于t>T的时候，我们固定学习率为n_T，不再增加。下边的例子中，T=20.

class CosineScheduler:
    def __init__(self, max_update, base_lr=0.01, final_lr=0,
               warmup_steps=0, warmup_begin_lr=0):
        self.base_lr_orig = base_lr
        self.max_update = max_update
        self.final_lr = final_lr
        self.warmup_steps = warmup_steps
        self.warmup_begin_lr = warmup_begin_lr
        self.max_steps = self.max_update - self.warmup_steps

    def get_warmup_lr(self, epoch):
        increase = (self.base_lr_orig - self.warmup_begin_lr) 
                       * float(epoch) / float(self.warmup_steps)
        return self.warmup_begin_lr + increase

    def __call__(self, epoch):
        if epoch < self.warmup_steps:
            return self.get_warmup_lr(epoch)
        if epoch <= self.max_update:
            self.base_lr = self.final_lr + (self.base_lr_orig - self.final_lr) * 
                    (1 + math.cos(math.pi * (epoch - self.warmup_steps) /
                                  self.max_steps)) / 2
        return self.base_lr


scheduler = CosineScheduler(max_update=20, base_lr=0.3, final_lr=0.01)
d2l.plot(tf.range(num_epochs), [scheduler(t) for t in range(num_epochs)])

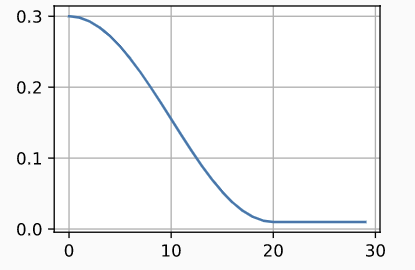
在CV领域，这个调度策略可以带来提升。但是，这个提升是无法被保障的。

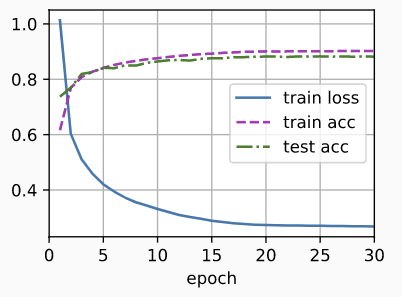
train(net, train_iter, test_iter, num_epochs, lr,
      custom_callback=LearningRateScheduler(scheduler))

4. Warmup

在某些情况下，初始化参数不足以保证一个好的解决方案。这对于一些高级网络设计来说尤其是一个问题，它可能导致不稳定的优化。我们可以通过选择足够小的学习率来解决这个问题，以防止在开始时出现发散。不幸的是，这意味着训练会很缓慢。相反，一个大的学习率最初会导致发散。解决这一困境的一个相当简单的方法是增加预热阶段，在预热阶段会将学习率提高到初始最大值。然后进入冷却阶段，直到优化过程结束。为了简单起见，通常使用线性增长来实现这一目的。就像如下展示的那样：

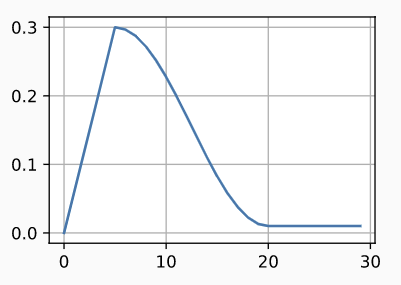
scheduler = CosineScheduler(20, warmup_steps=5, base_lr=0.3, final_lr=0.01)   # 前5步进行预热，直到base lr=0.3
d2l.plot(tf.range(num_epochs), [scheduler(t) for t in range(num_epochs)])

train(net, train_iter, test_iter, num_epochs, lr,
      custom_callback=LearningRateScheduler(scheduler))

从下图可以看出，前5步收敛的也很好

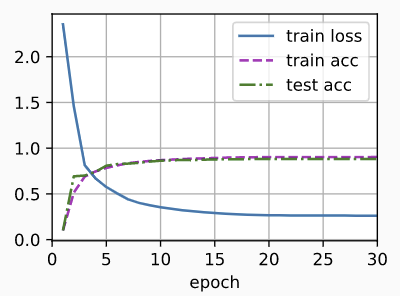
Warmup可以被用到任一调度器。有关学习率调度和更多实验的更详细讨论，请参见 A closer look at deep learning heuristics: learning rate restarts, warmup and distillation。特别是他们发现预热阶段限制了非常深的网络中参数的发散量。这是符合直觉的，因为我们预计在训练网络的初期，随机初始化会导致明显的发散，而这些部分在一开始就需要花费大量的时间进行优化。

总结

1. 训练期间降低学习率可以提升准确率，降低模型过拟合；
2. 在实践中，当学习进度停滞不前时，逐步降低学习率是有效的。本质上，这保证了我们有效地收敛到一个合适的解，并且只有这样才能通过降低学习速率来减少参数的变化幅度；
3. 余弦调度器在一些计算机视觉问题中很流行；
4. 优化前的预热期可以防止发散；
5. 优化过程在深度学习中有多种作用。除了尽量减少训练loss，优化算法和学习速率调度的不同选择会导致测试集上不同程度的泛化和过度拟合。