A.Find a Number

#include <iostream> #include <cstring> #include <queue> using namespace std; const int maxn=5007; struct S{ int len,mod,sum; char c[600];//别太大也别太小,打表测试600以内能跑出所有答案 S(){ len=mod=sum=0; memset(c,0,sizeof c);//太大这里会tle } }; bool vis[507][maxn]; void print(S x){ for (int i=0;i<x.len;i++) printf("%c",x.c[i]); printf(" "); } int main(){ int d,s; scanf("%d%d",&d,&s); S h; queue<S>q; q.push(h); while (!q.empty()){ h=q.front(); q.pop(); for (int i=0;i<=9;i++){ S x=h; x.c[x.len++]=i+'0'; x.sum+=i; x.mod=(x.mod*10+i)%d; if (x.sum>s||vis[x.mod][x.sum]) continue; vis[x.mod][x.sum]=1; if (x.mod==0&&x.sum==s){ print(x); return 0; } q.push(x); } } printf("-1 "); return 0; }
B.Berkomnadzor
C.Cloud Computing
Chen.Jr
一个很有意思的题目,首先我们可以想到一个简单的贪心的策略:将费用由小到大进行排序,然后优先在区间[l,r]内选取费用小的。
但是这样做的话,我们在处理区间个数以及费用的时候将会非常困难。
因为维护区间下标比较困难,因此我们可以考虑用权值线段树对权值进行维护。
我们分别对每一个权值维护权值存在的个数以及最终的花费。
对于每一个区间[l,r],我们只需要在位置l上+c,在位置 (r+1)上 -c,并对区间[1,n]的每一个位置都进行上述的更新。
最后我们只需要查询权值线段树上个数不大于K的节点,并统计答案即可。(查询过程中如果左儿子的个数下于k,则只需将答案加上左儿子的花费并再查询右儿子的个数不大于K-[左儿子个数]的节点即可)

#include <bits/stdc++.h> #define maxn 1000005 using namespace std; typedef pair<int,int>PLL; typedef long long ll; struct ST{ ll sum,cnt;//分别维护某节点的出现次数以及某节点的总花费 }tr[maxn<<2]; void update(int l,int r,int rt,ll num,ll val){//num为个数,val为值 tr[rt].sum+=num*val; tr[rt].cnt+=num; if(l==r) return ; int mid=(l+r)>>1; if(val<=mid) update(l,mid,rt<<1,num,val); else update(mid+1,r,rt<<1|1,num,val); } ll query(int l,int r,int rt,int K){//查询答案 if(l==r) return 1ll*l*K;//搜到了叶子节点,则直接返回结果(权值×k) int mid=(l+r)>>1; //如果左儿子的个数小于K,则直接统计左儿子的答案,并再询问右儿子的不大于k-左儿子个数 if(K>tr[rt<<1].cnt) return tr[rt<<1].sum+query(mid+1,r,rt<<1|1,K-tr[rt<<1].cnt); else return query(l,mid,rt<<1,K); } vector<PLL>vec[maxn]; int main() { // freopen("in.txt","r",stdin); int n,k,m; scanf("%d%d%d",&n,&k,&m); for(int i=0;i<m;i++){ int l,r,c,p; scanf("%d%d%d%d",&l,&r,&c,&p); //此过程为一个类似扫描线的过程 vec[l].push_back(make_pair(c,p)); vec[r+1].push_back(make_pair(-c,p)); } ll ans=0; for(int i=1;i<=n;i++){ int sz=vec[i].size(); for(int j=0;j<sz;j++){//更新在该位置上的所有值 update(1,maxn,1,vec[i][j].first,vec[i][j].second); } ans+=query(1,maxn,1,min(1ll*k,tr[1].cnt)); } cout<<ans<<endl; }
update by LQS:
非常显然的是,在每一个点的时候肯定是先选价值小的然后再选价值大的,训练的时候想过能不能二分来查找到最后一个数量和小于等于k的地方,但是这样的话还是没有办法对每一个点上覆盖的线段按价值排序。
数据范围p和c都是1e6,并且策略是先选价值小的,因此可以在遍历1到n号点的过程中以价值为下标做一个树状数组,借助差分的思想即可得到取到前若干小价值的时候数量的前缀和,于是这时就可以二分一下数量找到最后一个数量前缀和小于等于k的位置了,那么最后再判断一下是否加上下一个即可。这个做法的关键在于发现先选价值小的策略后,将权值转为下标,此时需要维护的东西就是做一个差分然后前缀和而已。

1 #include<bits/stdc++.h> 2 using namespace std; 3 const int maxn=1000005; 4 long long num[maxn]; 5 long long v[maxn]; 6 int lowbit(int x){return x&(-x);} 7 struct data{ 8 int num,val; 9 }; 10 vector<data>vec[1000005]; 11 void update1(int x,long long val){ 12 for(int i=x;i<maxn;i+=lowbit(i)) num[i]+=val; 13 } 14 long long query1(int x){ 15 long long ret=0; 16 for(int i=x;i>0;i-=lowbit(i)) ret+=num[i]; 17 return ret; 18 } 19 void update2(int x,long long val){ 20 for(int i=x;i<maxn;i+=lowbit(i)) v[i]+=val; 21 } 22 long long query2(int x){ 23 long long ret=0; 24 for(int i=x;i>0;i-=lowbit(i)) ret+=v[i]; 25 return ret; 26 } 27 void read(int &ret){ 28 ret=0; 29 char ch=getchar(); 30 while(ch>'9'||ch<'0') ch=getchar(); 31 while(ch>='0'&&ch<='9'){ 32 ret=ret*10+ch-'0'; 33 ch=getchar(); 34 } 35 } 36 void read(long long &ret){ 37 ret=0; 38 char ch=getchar(); 39 while(ch>'9'||ch<'0') ch=getchar(); 40 while(ch>='0'&&ch<='9'){ 41 ret=ret*10+ch-'0'; 42 ch=getchar(); 43 } 44 } 45 bool check(int x,int sum){ 46 if(query1(x)<=1LL*sum) return 1; 47 return 0; 48 } 49 int main(){ 50 //freopen("in.txt","r",stdin); 51 int n,k,m; 52 int l,r; 53 long long c,p; 54 read(n),read(k),read(m); 55 int up=0; 56 for(int i=1;i<=m;i++){ 57 read(l),read(r),read(c),read(p); 58 up=max(1LL*up,p); 59 vec[l].push_back(data{c,p}); 60 vec[r+1].push_back(data{-c,p}); 61 } 62 long long ret=0; 63 for(int i=1;i<=n;i++){ 64 for(int j=0;j<vec[i].size();j++){ 65 update1(vec[i][j].val,vec[i][j].num); 66 update2(vec[i][j].val,1LL*vec[i][j].num*vec[i][j].val); 67 } 68 l=0,r=up; 69 int ans=0; 70 while(l<=r){ 71 int mid=(l+r)>>1; 72 if(check(mid,k)){ans=mid;l=mid+1;} 73 else r=mid-1; 74 } 75 long long sum1=query1(ans); 76 long long sum2=query2(ans); 77 ret+=sum2; 78 if(ans<up) ret+=1LL*(ans+1)*(k-sum1); 79 } 80 printf("%lld ",ret); 81 }
D.Garbage Disposal
温暖的签到题,同样注意一下细节即可。

#include<bits/stdc++.h> using namespace std; long long a[200005]; int main(){ //freopen("in.txt","r",stdin); int n,k; scanf("%d%d",&n,&k); for(int i=1;i<=n;i++) scanf("%lld",&a[i]); long long pre=0; long long ans=0; for(int i=1;i<=n;i++){ if(a[i]+pre<=k&&pre){ ans++; pre=0; continue; } a[i]+=pre; ans+=a[i]/k; pre=a[i]%k; } if(pre) ans++; printf("%lld ",ans); return 0; }
E.Getting Deals Done
看到这道题第一眼的感觉就是d貌似可以二分答案出来,但是很快就会发现如果二分答案d的话,直接check是错的。应该看出来,一个可能的d必然会是某个题目的难度值,这样的话,如果二分答案时以这个难度值为d,难度值小于等于d的题目都是可做的,这样就出现的单调性。也就是说只要做完所有难度小于等于d的题目的时间小于等于t,那么这个d就可以是答案,这也就是check的方法。

1 #include<bits/stdc++.h> 2 using namespace std; 3 const int maxn=200005; 4 int a[maxn],s[maxn]; 5 int n,m,C; 6 long long t; 7 void read(long long &ret){ 8 ret=0; 9 char ch=getchar(); 10 while(ch>'9'||ch<'0') ch=getchar(); 11 while(ch<='9'&&ch>='0'){ 12 ret=ret*10+ch-'0'; 13 ch=getchar(); 14 } 15 } 16 void read(int &ret){ 17 ret=0; 18 char ch=getchar(); 19 while(ch>'9'||ch<'0') ch=getchar(); 20 while(ch<='9'&&ch>='0'){ 21 ret=ret*10+ch-'0'; 22 ch=getchar(); 23 } 24 } 25 bool check(int x){ 26 long long sum=0; 27 long long tmp=0; 28 int d=s[x],cnt=0; 29 for(int i=1;i<=n;i++){ 30 if(cnt==x) break; 31 if(a[i]<=d){ 32 if(cnt&&cnt%m==0){sum+=tmp;tmp=0;} 33 sum+=a[i]; 34 tmp+=a[i]; 35 cnt++; 36 } 37 } 38 return sum<=t; 39 } 40 int main(){ 41 read(C); 42 while(C--){ 43 read(n),read(m),read(t); 44 for(int i=1;i<=n;i++) {read(a[i]);s[i]=a[i];} 45 sort(s+1,s+n+1); 46 s[0]=1; 47 int l=1,r=n; 48 int ans=0; 49 while(l<=r){ 50 int mid=(l+r)>>1; 51 if(check(mid)){ans=mid;l=mid+1;} 52 else r=mid-1; 53 } 54 printf("%d %d ",ans,s[ans]); 55 } 56 return 0; 57 }
F.Debate
考虑贪心。
不难发现11必定可以选取,因此首先先将所有的11选了。
其次发现01和10如果两两一起选的话,也不影响答案。因此贪心的将01和10从大往小选取。
最后只需要再特判以下00的状态是否可选即可。

#include<bits/stdc++.h> using namespace std; const int maxn=400005; int num[4][maxn]; int sum[4][maxn]; char op[2]; int cnt[4]; priority_queue<int>q; bool cmp(int a,int b){ return a>b; } int main(){ //freopen("in.txt","r",stdin); int n; scanf("%d",&n); for(int i=1;i<=n;i++){ scanf("%s",op); if(op[0]=='0'){ if(op[1]=='0'){ scanf("%d",&num[0][++cnt[0]]); q.push(num[0][cnt[0]]); } else scanf("%d",&num[1][++cnt[1]]); }else{ if(op[1]=='0')scanf("%d",&num[2][++cnt[2]]); else scanf("%d",&num[3][++cnt[3]]); } } for(int i=0;i<=3;i++){ sort(num[i]+1,num[i]+cnt[i]+1,cmp); for(int j=1;j<=cnt[i];j++) sum[i][j]=sum[i][j-1]+num[i][j]; } int ans=0; ans+=sum[3][cnt[3]]; int n1=0; if(cnt[1]>cnt[2]){ n1=cnt[2]; for(int i=n1+1;i<=cnt[1];i++) q.push(num[1][i]); }else if(cnt[2]>cnt[1]){ n1=cnt[1]; for(int i=n1+1;i<=cnt[2];i++) q.push(num[2][i]); }else n1=cnt[1]; ans+=sum[1][n1]+sum[2][n1]; int le=cnt[3]; while(le&&!q.empty()){ ans+=q.top(); q.pop(); le--; } printf("%d ",ans); return 0; }
G.Monsters and Potions
题目相当臭长,但是如果能够静下心来读懂意思的话,貌似也不是不可做的。
我们可以先n^2预处理出每个英雄能移动的范围每个英雄能移动的范围,然后枚举集结点,暴力对每个集结点进行判断它是否可行,注意细节判断,要特别注意,集结点位置如果是怪物,你要让左边的英雄杀它还是右边的英雄杀它。

#include<bits/stdc++.h> using namespace std; const int maxn=107; int mp[maxn][maxn]; int a[maxn],n,m,s[maxn],h[maxn],vis[maxn],id[maxn]; int ans[maxn],cnt; void init(){//n^2预处理每个英雄能移动的范围 for (int i=1;i<=m;i++){ mp[s[i]][s[i]]=h[i]; int tmp=h[i]; for (int j=s[i];j>=1;j--){ if (tmp<0) mp[s[i]][j]=-1; else { tmp+=a[j]; mp[s[i]][j]=max(-1,tmp); } } tmp=h[i]; for (int j=s[i];j<=n;j++){ if (tmp<0) mp[s[i]][j]=-1; else { tmp+=a[j]; mp[s[i]][j]=max(-1,tmp); } } } } void print(int x){//打印答案 printf("%d ",x); for (int i=1;i<=m;i++){ if (!vis[i]) ans[++cnt]=i; } for (int i=1;i<cnt;i++) printf("%d ",ans[i]); printf("%d ",ans[cnt]); } bool check(int x,int y){// 查找剩余区间是否有英雄 for (int i=x;i<=y;i++){ if (id[i]) return 0; } return 1; } int main(){ //freopen("in.txt","r",stdin); scanf("%d %d",&n,&m); for (int i=1;i<=m;i++) { scanf("%d%d",&s[i],&h[i]); id[s[i]]=i; } for (int i=1;i<=n;i++) scanf("%d",&a[i]); init(); a[0]=a[n+1]=0; for (int i=1;i<=n;i++){//枚举集结点 // 将集结点归在左区间 memset(vis,0,sizeof vis); int tmp=i;//目前走到的位置 cnt=0; bool f=0;//标记集结点是否走过 for (int j=i;j>=1;j--){ if (id[j]&&mp[j][tmp]>=0){ vis[id[j]]=1; ans[++cnt]=id[j]; tmp=j-1; f=1; } } if (check(0,tmp)){ if (f==0) tmp=i; else tmp=i+1; for (int j=tmp;j<=n;j++){ if (id[j]&&mp[j][tmp]>=0){ vis[id[j]]=1; ans[++cnt]=id[j]; tmp=j+1; } } if (check(tmp,n+1)){ print(i); return 0; } } //将集结点归在右区间 memset(vis,0,sizeof vis); cnt=0; tmp=i;f=0; for (int j=i;j<=n;j++){ if (id[j]&&mp[j][tmp]>=0){ vis[id[j]]=1; ans[++cnt]=id[j]; tmp=j+1; f=1; } } if (check(tmp,n+1)){ if (f==0) tmp=i; else tmp=i-1; for (int j=tmp;j>=1;j--){ if (id[j]&&mp[j][tmp]>=0){ vis[id[j]]=1; ans[++cnt]=id[j]; tmp=j-1; } } if (check(0,tmp)){ print(i); return 0; } } } printf("-1 "); return 0; }
H.BerOS File Suggestion
因为每一个字符串相当的小,因此我们直接可以暴力获得每一个字符串的字串,并用两个map对这些字串分别映射一下即可。

#include<bits/stdc++.h> using namespace std; unordered_map<string,int>ans; unordered_map<string,string>anss; unordered_map<string,int>vis; string str; string tmp; int main(){ ios::sync_with_stdio(false); cin.tie(0); //freopen("in.txt","r",stdin); int n; cin>>n; for(int i=1;i<=n;i++){ cin>>str; int len=str.length(); vis.clear(); for(int i=0;i<len;i++){ for(int j=1;i+j<=len;j++){ tmp=str.substr(i,j); if(vis.count(tmp)) continue; vis[tmp]=1; ans[tmp]++; anss[tmp]=str; } } } int q; cin>>q; for(int i=1;i<=q;i++){ cin>>str; if(ans.count(str)){ cout<<ans[str]<<" "<<anss[str]<<endl; }else{ cout<<"0 -"<<endl; } } return 0; }
I.Privatization of Roads in Berland
J.Streets and Avenues in Berhattan
首先要理解好题意;
题意是说有n条横线,m条竖线,现在有一个长度为k的只有'A'到‘Z’构成字符串。现在要让你将这k个字符串的部分字符分配到每一个横线和每一个竖线上。而当某一条横线i与一条竖线j他们发生相交,在他们分配到的每一个字符种,每有一种字符的种类相同,不开心值+1。现在你要对这K个字符串进行分配,现问你最小的不开心值为多少。
明白了题意之后,不难发现,对于任意一条横线和任意一条竖线,他们必定会发生相交。因此和n条横线对答案的贡献其实是等价的(竖线同理)。因此这个问题就转化成了,有两个集合A(A要分配n个字符)和B(B要分配m个字符),你要将这K个字符串分配到这两个集合中,问你采取何种策略,可以使得在分配后的两个集合中,对于任意的i,求出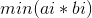
由此我们发现,最终的结果仅与某一种字符有关。因此我们可以先统计出每种字串出现的次数,然后枚举每一种字符。对于每一种字符,我们可以通过01背包进行转移判断取j个第i种字符是否可行,最后我们再枚举ai的数量,不断维护最小值即可。

#include <bits/stdc++.h> #define maxn 30005 #define maxm 200005 using namespace std; typedef long long ll; int dp[maxn],cnt[30]; //dp[i]代表对于某一种物品,能够取i个 char str[maxm]; int main() { int t; scanf("%d",&t); while(t--){ int n,m,k; ll ans=0x3f3f3f3f3f3f3f3f; scanf("%d%d%d",&n,&m,&k); memset(cnt,0,sizeof(cnt)); scanf("%s",str); int len=strlen(str); for(int i=0;i<len;i++) cnt[str[i]-'A'+1]++; for(int i=1;i<=26;i++){ for(int j=1;j<=n;j++) dp[j]=0; dp[0]=1; for(int j=1;j<=26;j++){//01 bag if(i==j) continue; for(int k=n;k>=cnt[j];k--){ dp[k]|=dp[k-cnt[j]]; } } for(int j=min(cnt[i],n);j>=0;j--){//枚举答案个数 if(!dp[n-j]) continue; ans=min(ans,1ll*j*(max(0ll,1ll*cnt[i]-j-k+m+n)));//统计答案 } } cout<<ans<<endl; } }
K.Video Posts
温暖的签到题,注意特殊情况的特判即可。

#include<bits/stdc++.h> using namespace std; const int maxn=1e5+7; typedef long long ll; ll a[maxn],ans[maxn]; int main(){ // freopen("in.txt","r",stdin); ll n,k,sum=0; scanf("%lld%lld",&n,&k); for (int i=1;i<=n;i++) { scanf("%lld",a+i); sum+=a[i]; } if (sum%k) { printf("No "); return 0; } ll cnt=sum/k,tmp,res=0,id=0; for (int i=1;i<=n;i++){ tmp+=a[i];res++; if (tmp>cnt){ printf("No "); return 0; }else if (tmp==cnt){ ans[++id]=res; res=tmp=0; } } printf("Yes "); for (int i=1;i<k;i++) printf("%lld ",ans[i]); printf("%lld ",ans[k]); return 0; }
L.Odd Federalization
M.Algoland and Berland
