拒绝采样

高斯分布的PDF：

$f(x)= frac{1}{sigmasqrt{2pi}} e^{-frac{(x-mu)^{2}}{2sigma^{2}}}$

其中$mu$是期望，$sigma^2$为标准方差，记为$X sim mathcal{N}(0,0.5)$

*****样本容量无限增大，分组的组距无限缩小，那么频率分布直方图，就会无限接近于一条光滑曲线，即总体密度曲线PDF*************

如：

---

给定一个分布$p(z)$,对该分布进行拒绝采样，首先定义个proposal distribution，定义为q(z), 这个分布是比较容易实现的，如高斯分布、均匀分布.

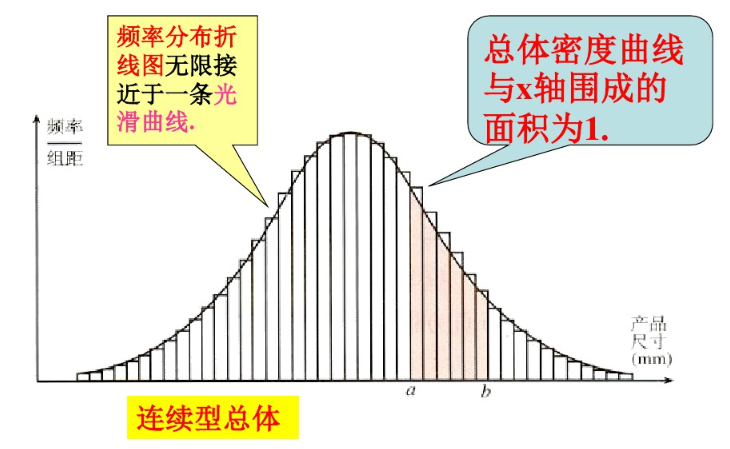
首先从这个简单的分布采样一些点出来，我们这里假设从一个高斯分布中采样点，$ extit{X} sim mathcal{N}(1.4,1.2)$, 代码实现：

 z = np.random.normal(loc = 1.4,scale = 1.2, size = size) // size = 1e7

做频率直方图：

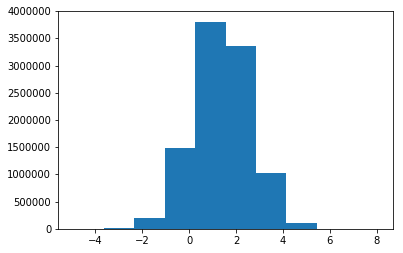
 之后将采样的点，带入到q(z)中，得到一些采样点对应的density,即$q(X_{i})$,相当于通过采样的点，再反过来刻画出PDF，做频率直方图：

qz = 1/(np.sqrt(2*np.pi)*sigma)*np.exp(-0.5*(z-1.4)**2/sigma**2)

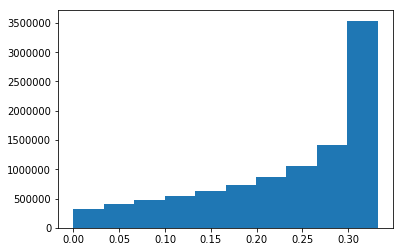
之后以x轴对每个采样点画一条线，从0到这个采样点对应的q(x)的值这个线进行均匀采样，$a sim Uniform(0,q(X_{i}))$，很明显如果采样点对应的p(x)越小，通过这样得到的均匀分布的采样点就越不可能

落在p(x)的下方，反之亦然：

k = 2.5 //k表示把整个分布抬高，使得整个proposal 分布能够cover掉这个p(x)
u = np.random.uniform(low = 0, high = k*qz, size = size)
pz =  0.3*np.exp(-(z-0.3)**2) + 0.7* np.exp(-(z-2.)**2/0.3)

 

上面的M就是代码中的k，结果就是如果得到的u小于对应的p(x)的值，则被接收，否则被拒绝。

****需要主要的是*******

1. 接受率=p(x)/Mq(x) M是来控制均匀分布的高度

2.简单的分布q(x)总是覆盖想要得到的分布吗？我们可以将M设置为非常大的number,Mq(x)可以接收的点，就会很少，大多数的点都被拒绝了,接受率非常小，不够高效， 所以q(x)的选择非常重要.

3.p(x)一定要cover掉q(x)