二维坐标系中的点积、叉积、多边形面积
点积定义
设有向量 (vec{a}) 和 (vec{b}) ,定义点积 (vec{a}cdot vec{b}) 为 实数 ,其值为 向量 (vec{a}) 在向量 (vec{b}) 上投影的长度乘以向量 (vec{b}) 的模
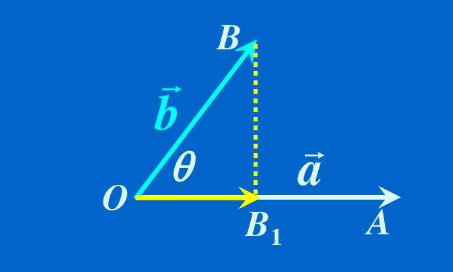
点积性质
满足交换律,结合律
点积计算
直接计算
坐标系中计算
放在坐标系中,设 (vec{a} = (x_{1}, y_{1}), vec{b} = (x_{2}, y_{2}))
那么 (vec{a}cdot vec{b} = x_{1}x_{2} + y_{1}y_{2})
叉积定义
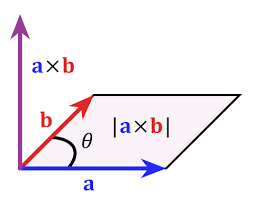
设有向量 (vec{a}) 和 (vec{b}) ,定义叉积 (vec{a} imes vec{b}) 为新的 向量。
其模长为 (vec{a}) 和 (vec{b}) 所围成的平行四边形面积。
方向与 (vec{a}) 和 (vec{b}) 均垂直。
若 (vec{b}) 在 (vec{a}) 逆时针方向,即呈现左手系,那么 (vec{a} imes vec{b}) 为正;反之为负。
叉积性质
叉积模即为平行四边形面积,所以在直角坐标系中求一个三角形的面积可以用叉积来计算,即
叉积不满足交换律,因为方向会发生变化,即
二维叉积模的计算
直接计算
坐标系中计算
放在坐标系中,设 (vec{a} = (x_{1}, y_{1}), vec{b} = (x_{2}, y_{2}))
经过推导得到 (|vec{a} imes vec{b}| = |x_{1}y_{2} - x_{2}y_{1}|)
去掉绝对值便得到 有向面积
若值为正,说明 (vec{b}) 在 (vec{a}) 逆时针方向;若值为负,说明说明 (vec{b}) 在 (vec{a}) 顺时针方向。
多边形面积计算
基本思想是把多边形划分成多个三角形,然后叉积计算面积。这个思想对于凹凸多边形都成立。
记多边形顶点逆时针排列为 (P_{0}, P_{1}, .., P_{n - 1})
为了方便计算,选取坐标原点 (O(0, 0)) 作为源点,逐一计算 (vec{OP_{i}} imes vec{OP_{i + 1}}) ,累计求和即可。
公式为
当 (i = n - 1) 时,下一个坐标要回到 ((x_{0}, y_{0})) ,这里可以特判,也可以取模运算。
复杂度 (O_{n})
由于叉积面积的有向性,多余的面积会被抵消掉,所以这个算法是正确的,此处省略严格证明。
(code)
int n;
struct Cor
{
int x, y;
}cor[105];
inline int read()
{
char c = getchar();
int ans = 0, f = 1;
while(!isdigit(c)) {if(c == '-') f = -1; c = getchar();}
while(isdigit(c)) {ans = ans * 10 + c - '0'; c = getchar();}
return ans * f;
}
int main()
{
while(scanf("%d", &n) && n) {
for(int i = 0; i < n; ++i)
cor[i].x = read(), cor[i].y = read();
double ans = 0.0;
for(int i = 0; i < n; ++i){
ans += 0.5 * (cor[i % n].x * cor[(i + 1) % n].y - cor[i % n].y * cor[(i + 1) % n].x);
}
printf("%.1f
", ans);
}
return 0;
}