四个复杂度分析方面的知识点:最好情况时间复杂度(best case time complexity)、最坏情况时间复杂度(worst case time complexity)、平均情况时间复杂度(average case time complexity)、均摊时间复杂度(amortized time complexity)。
一、复杂度分析的4个概念
1.最坏情况时间复杂度:代码在最理想情况下执行的时间复杂度。
2.最好情况时间复杂度:代码在最坏情况下执行的时间复杂度。
3.平均时间复杂度:用代码在所有情况下执行的次数的加权平均值表示。
4.均摊时间复杂度:在代码执行的所有复杂度情况中绝大部分是低级别的复杂度,个别情况是高级别复杂度且发生具有时序关系时,可以将个别高级别复杂度均摊到低级别复杂度上。基本上均摊结果就等于低级别复杂度。
二、为什么要引入这4个概念?
1.同一段代码在不同情况下时间复杂度会出现量级差异,为了更全面,更准确的描述代码的时间复杂度,所以引入这4个概念。
2.代码复杂度在不同情况下出现量级差别时才需要区别这四种复杂度。大多数情况下,是不需要区别分析它们的。
三、如何分析平均、均摊时间复杂度?
1.平均时间复杂度
代码在不同情况下复杂度出现量级差别,则用代码所有可能情况下执行次数的加权平均值表示。
2.均摊时间复杂度
两个条件满足时使用:1)代码在绝大多数情况下是低级别复杂度,只有极少数情况是高级别复杂度;2)低级别和高级别复杂度出现具有时序规律。均摊结果一般都等于低级别复杂度。
最好最坏时间复杂度:在无序数组中查找变量x的位置,最好的情况是,第一个就是我们要找的元素,时间复杂度O(1),最坏的情况是,把数据都遍历了一遍,仍旧找不到数据x,时间复杂度O(n)。
平均时间复杂度:最好情况、最坏情况时间复杂度对应的都是极端情况下的代码复杂度,发生的概率其实并不大。为了更好地表示平均情况下的复杂度,引入了概念:平均情况时间复杂度,即平均时间复杂度。
要查找的变量x在数组中的位置,有n+1中情况:在数组0~n-1位置中和不在数组中。查找需要遍历的元素个数加起来,然后再除以n+1,就可以得到需要遍历的元素个数的平均值,即:
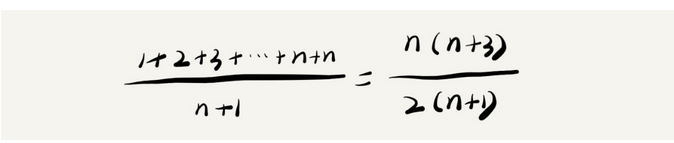
时间复杂度的大O标记法中,可以忽略系数、低阶、常量,所以,平均时间复杂度为O(n)。
这个结论是正确的,但是计算过程稍微有点儿问题。问题是什么呢?我们刚讲的这n+1中情况,出现的概率是不一样的。我们知道,我们要查找的元素x,有在数组中和不在数组中两种情况。这两种情况对应的概率都为1/2,另外0~n-1中出现x的概率是一样的,都为1/n,所以,要查找的数据出现在0~n-1中任意位置的概率为1/(2n)。因此,考虑进了发生概率之后,平均时间复杂度的甲酸过程就变成了下图:
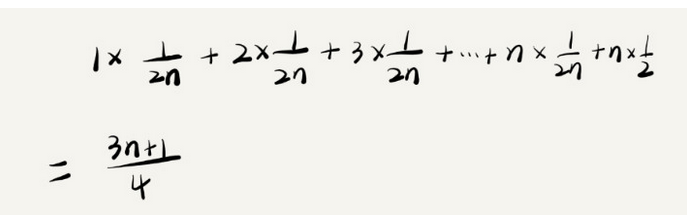
这个值就是加权平均值,也叫作期望值,所以平均时间复杂度的全称应该叫作甲醛平均时间复杂度或者期望时间复杂度。此时用大O表示法来表示,去掉系数和常量,这段代码的加权平均时间复杂度仍然是O(n)。
课后思考
分析一下下面add()函数的时间复杂度。
1 int array[] = new int[10]; 2 int len = 10; 3 int i = 0; 4 void add(int element){ 5 if(i>=len){//数组空间不够,重新申请一个2倍大的数组空间 6 int new_array[] = new int[len*2]; 7 //把原来array数组中的数据依次copy到new_array 8 for(int j=0; j<len; j++){ 9 new_array[j] = array[j]; 10 } 11 12 //new_array复制到array,array就是2倍大小的len了 13 array = new_array; 14 len = 2*len; 15 16 } 17 18 //将element放到下标为i的位置,下标加一 19 array[i] = element; 20 ++i; 21 }