第一部分 现代_3 线性映射

第三章 线性映射

1、线性空间

（1）向量空间

 

 （2）线性空间

说明：

a：当同时满足加法运算（即封闭）和数量乘法（八条运算法则）才能说明V是数域F上的线性空间；

b：第三条运算法则中的0元素并不是指特定的0向量，只要满足第三条运算法则的元素都是0元素-----同理，第四条运算法则中的- 是一样的；

（3）线性空间的基与维数

 

 

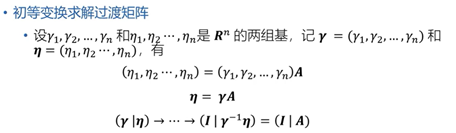
2、线性空间

 

 

 

总结（对应以上3种常见的线性变换）：

a：线性变化保持数乘

b：实质上是进行了正交变换

c：微分运算保持加法和数乘运算

 线性变换的矩阵表示：

 

某向量在进行线性变换后的关系：

因为线性变换的基是对于选定的矩阵来说的，所以探索不同基下的矩阵之间的关系是很有必要的。