3、 多维随机变量的分布
（1）多项分布
可参见https://blog.csdn.net/jteng/article/details/54632311
多项分布是对二项分布的扩展，二项分布是单变量分布，而多项分布式多变量分布。
二项分布每次试验试验只有两种结果，而多项分布每次试验则会有多种可能性，那么进行多次的试验后，多项分布描述的就是每种可能发生次数的联合概率分布。
（2）Gamma函数
首先说一下先验概率和后验概率的区别，然后再进行下面的步骤：
验前概率就是通常说的概率；
验后概率是一种条件概率，但条件概率不一定是验后概率；
我们常用的贝叶斯公式就是由验前概率求延后概率的公式；
举一个简单的例子：一口袋里有3只红球、2只白球，采用不放回方式摸取，求：
⑴ 第一次摸到红球（记作A）的概率；
⑵ 第二次摸到红球（记作B）的概率；
⑶ 已知第二次摸到了红球，求第一次摸到的是红球的概率。
解：
⑴ P(A)=3/5，这就是验前概率；
⑵
P(B)=P(A)P(B|A)+P(A逆)P(B|A逆)=(3/5)×(1/2)+(2/5)×(3/4)
= 3/5
⑶
P(A|B)=P(A)P(B|A)/P(B)=(3/5)×(1/2)/(3/5)=1/2，这就是验后概率。
Beta分布于Dirichlet分布的定义域均为【0,1】，在实际生活中，Beta分布描述的是单变量分布，Dirichlet分布描述的是多变量分布。
于是乎，Beta分布可以作为二项分布的先验概率，Dirichlet分布可以作为多项分布的先验概率。
由于这两个分布均用到了Gamma函数，所以必须先了解Gamma函数。
Gamma函数的表达式为
其中，x>0
Gamma函数有如下性质：
具体推导如下：
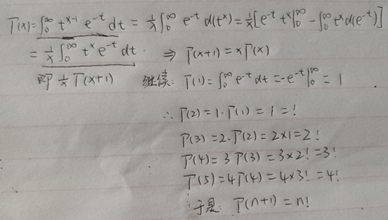
Gamma函数在Beta分布和Dirichlet分布中起到了归一化的作用。
1）Beta分布
与连续随机变量的分布不同，Beta分布描述的是定义在区间【0,1】上随机变量的概率分布，由两个参数
其概率密度函数为
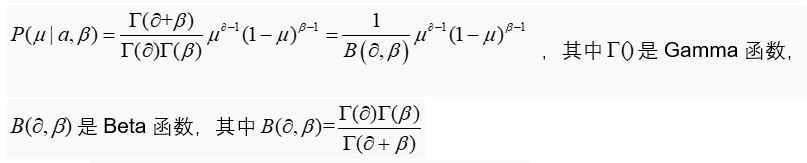
（1） 当
均 >1时，Beta分布为上凸的单峰曲线；
（2）当一个大于1，一个小于1时，Beta分布为下凸的的单调函数；
（3）当均 = 1时，Beta分布为常数函数
Beta分布的概率密度曲线如下所示：
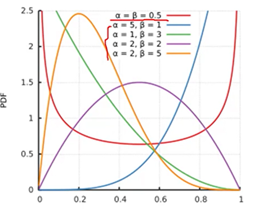
说明：由于Beta分布式定义在区间【0,1】上的，所以适合作为概率的分布（例如机器的维修率、市场的占有率等等）
Beta分布的均值和方差分别为：
2）狄利克雷分布（Dirichlet分布）
Dirichlet分布的每一个随机变量的统计量如下：
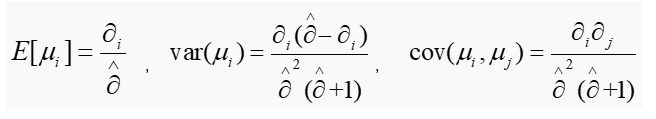
说明：由于Dirichlet分布描述的是多个定义在区间【0,1】上的随机变量的概率分布，所以通常将其用作多项分布参数 的概率分布。
（3）二维随机变量
1）二维连续随机变量
2）二维离散随机变量
（4）二维连续分布
1）二维均匀分布
设G是平面上的有界区域，其面积为A,若二维随机随机变量(X,Y)具有如下的概率密度函数，
向平面上有界区域G上任意投一个质点，如果质点落在G内任意一个小区域B的概率与小区域的面积成正比，与小区域B的形状与位置无关，那么质点的坐标（X,Y）在G上服从均匀分布。
2）二维正态分布
说明：
表示X和Y之间的相关系数。
二维正态分布的边缘密度还是一维的正态分布：
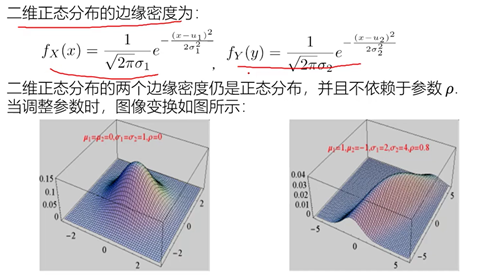
相互独立的两个一维正态构成的二位随机变量是服从二维正态的。