[Luogu] P3376 模板-网络流-最大流

题目描述

如题，给出一个网络图，以及其源点和汇点，求出其网络最大流。

输入输出格式

输入格式：

第一行包含四个正整数N、M、S、T，分别表示点的个数、有向边的个数、源点序号、汇点序号。

接下来M行每行包含三个正整数ui、vi、wi，表示第i条有向边从ui出发，到达vi，边权为wi（即该边最大流量为wi）

输出格式：

一行，包含一个正整数，即为该网络的最大流。

输入输出样例

输入样例#1：

4 5 4 3
4 2 30
4 3 20
2 3 20
2 1 30
1 3 40

输出样例#1：

50

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=10，M<=25

对于70%的数据：N<=200，M<=1000

对于100%的数据：N<=10000，M<=100000

样例说明：

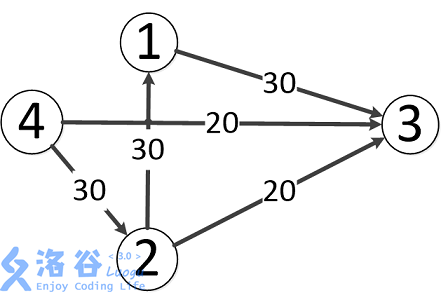
题目中存在3条路径：

4-->2-->3，该路线可通过20的流量

4-->3，可通过20的流量

4-->2-->1-->3，可通过10的流量（边4-->2之前已经耗费了20的流量）

故流量总计20+20+10=50。输出50。

分析

这是一个单纯的题目，优化都不用

= =然而我是对着刘汝佳写过去的

网络流还是推荐紫书

代码

//事先声明，这份代码并不是原创，只是将刘汝佳的进行风格转化
//数组模拟版本邻接表= =刘汝佳写的虽然简练但是我不是很习惯
#include<cstdio>
#include<iostream>
#include<queue>
#include<cstring>
#define maxn 10000000
using namespace std;

int inf = 2139999999;

struct edge{
    int from,u,v,cup,flow;
}e[maxn];

int tot = 2,first[maxn*4];
void insert(int u,int v,int ccup){
    e[tot].from = first[u];
    e[tot].u = u;
    e[tot].v = v;
    e[tot].cup = ccup;
    e[tot].flow = 0;
    first[u] = tot;
    tot++;
    
    e[tot].from = first[v];
    e[tot].u = v;
    e[tot].v = u;
    e[tot].cup = e[tot].flow = 0;
    first[v] = tot;
    tot++;
}

int pre[maxn],s,t,a[maxn],n,m;
int maxflow(int s,int t){
    
    int flow = 0;
    while(true){
//        cout << "gua!  ";
        memset(a,0,sizeof(a));
        queue<int> Q;
        Q.push(s);
        a[s] = inf;
        while(!Q.empty()){
//            cout << "Meow!  ";
            int p = Q.front(); Q.pop();
            
            for(int i = first[p];i;i = e[i].from){
                edge &E = e[i];
                if(!a[E.v] && E.flow < E.cup){
                    pre[E.v] = i;
                    a[E.v] = min(a[p],E.cup-E.flow);
                    Q.push(E.v);
                }
            }
            
            if(a[t]) break;
        }
        
        if(!a[t]) break;
        
        for(int u = t;u != s;u = e[pre[u]].u){
            e[pre[u]].flow += a[t];
            e[pre[u]^1].flow -= a[t];
        }
        
        flow += a[t];
    }
    
//    for(int i = 0;i <= n;i++){
//        printf("%d ",a[i]);
//    }cout << endl;
    
    return flow;
}

int main(){
    scanf("%d%d%d%d",&n,&m,&s,&t);
    
    for(int i = 1;i <= m;i++){
        int u,v,ccup;
        scanf("%d%d%d",&u,&v,&ccup);
        insert(u,v,ccup);
    } 
    
    cout << maxflow(s,t);
    
//    for(int i = 0;i <= tot;i++){
//        printf("%d %d %d %d %d
",e[i].from,e[i].u,e[i].v,e[i].cup,e[i].flow);
//    }
    
    return 0;
}