首先回顾一下交叉熵:
Softmax层的作用是把输出变成概率分布,假设神经网络的原始输出为y1,y2,….,yn,那么经过Softmax回归处理之后的输出为:

交叉熵刻画的是实际输出(概率)与期望输出(概率)的距离,也就是交叉熵的值越小,两个概率分布就越接近。假设概率分布p为期望输出(correct value),概率分布q(predicated value)为实际输出,H(p,q)为交叉熵,则:
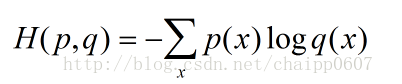
这个公式如何表征距离呢,举个例子:
假设N=3,期望输出为p=(1,0,0),实际输出q1=(0.5,0.2,0.3),q2=(0.8,0.1,0.1),

很显然,q2与p更为接近,它的交叉熵也更小。
交叉熵还有另一种表达形式,还是使用上面的假设条件:
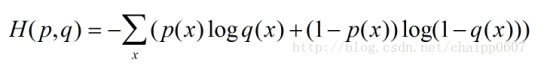
根据之前的假设:
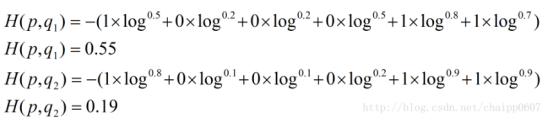
接下来看weighted loss:
weighted loss一般用作图像分割领域,尤其是在分割的边缘像素和非边缘像素样本数量不均匀,差别过大,导致的loss影响,学习较慢,精确率较低的问题。
weighted loss增加了一个参数来控制正样本和负样本的loss,公式如下: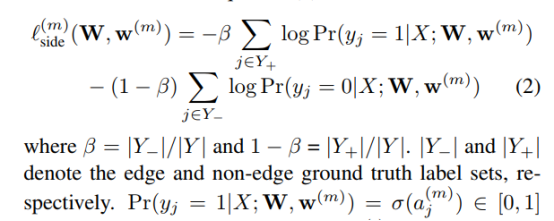
举个例子来说,比如一共100个像素,边缘像素有2个,非边缘有98个,那么边缘损失的权重为0.98,非边缘损失的权重为0.02,给数量少的正样本足够大的权重,卷积网络就可训练出最后满意结果。
接下来再看Focal loss,根据何大神的论文:
交叉熵2分类公式1:
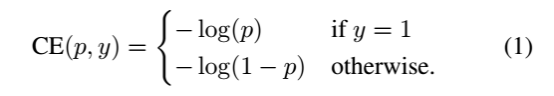
因为是二分类,所以y的值是正1或负1,p的范围为0到1。当真实label是1,也就是y=1时,假如某个样本x预测为1这个类的概率p=0.6,那么损失就是-log(0.6),注意这个损失是大于等于0的。如果p=0.9,那么损失就是-log(0.9),所以p=0.6的损失要大于p=0.9的损失.
为了方便用pt 表示下列公式2:

接下来对交叉熵进行了改进,公式3:增加了一个系数αt,跟Pt的定义类似,当label=1的时候,αt=α;当label=-1的时候,αt=1-α,α的范围也是0到1:
因此可以通过设定α的值(一般而言假如1这个类的样本数比-1这个类的样本数多很多,那么a会取0到0.5来增加-1这个类的样本的权重)来控制正负样本对总的loss的影响程度
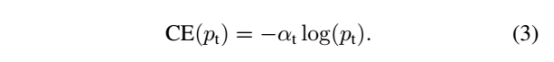
显然前面的公式3虽然可以控制正负样本的权重,但是没法控制容易分类和难分类样本的权重,于是就有了focal loss,公式4:
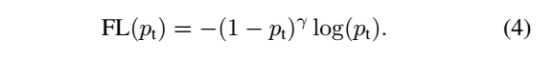
这里的γ称作focusing parameter,γ>=0。 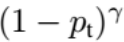 称为调制系数(modulating factor)
称为调制系数(modulating factor)
这里介绍下focal loss的两个重要性质:1、当一个样本被分错的时候,pt是很小的(请结合公式2,比如当y=1时,p要小于0.5才是错分类,难分类样本,此时pt就比较小,反之亦然),因此调制系数就趋于1,也就是说相比原来的loss是没有什么大的改变的。当pt趋于1的时候(此时分类正确而且是易分类样本),调制系数趋于0,也就是对于总的loss的贡献很小。2、当γ=0的时候,focal loss就是传统的交叉熵损失,当γ增加的时候,调制系数也会增加。
focal loss的两个性质算是核心,其实就是用一个合适的函数去度量难分类和易分类样本对总的损失的贡献。
作者在实验中采用的是公式5的focal loss(结合了公式3和公式4,这样既能调整正负样本的权重,又能控制难易分类样本的权重):
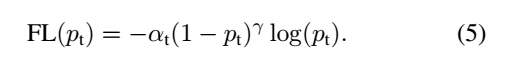
转载from https://blog.csdn.net/u014380165/article/details/77019084