数据结构与算法——b站学习笔记
引入:
先来看一道题:
如果a+b+c=1000,且a^2+b^2=c^2(a,b,c为自然数),如何求出所有a,b,c可能的组合?
算法:
计算机处理信息的本质,因为计算机程序本质是一个算法来告诉计算机确切的步骤来执行一个制定的任务。
算法是一个独立存在的一种解决问题的方法和思想。
对于算法而言,重要的不是实现它的编程语言,重要的是思想。
算法可以有不同的描述实现版本(C描述、C++描述、python描述)
算法有五大特性:
1、输入:算法具有0或多个输入
2、输出:至少有一个或多个输出
3、有穷性:在有限的步骤和可接受的时间内自动结束,不会陷入死循环
4、确定性:每一步都要有确定的含义,不能带有歧异
5、可行性:每一步都是可行的
算法效率衡量
结合上面的题目,引入两个算法:
1 import time 2 start_time = time.time() 3 # 注意是三重循环 4 for a in range(0, 1001): 5 for b in range(0, 1001): 6 for c in range(0, 1001): 7 if a**2 + b**2 == c**2 and a+b+c == 1000: 8 print("a, b, c: %d, %d, %d" % (a, b, c)) 9 10 end_time = time.time() 11 print("elapsed: %f" % (end_time - start_time)) 12 print("complete!")
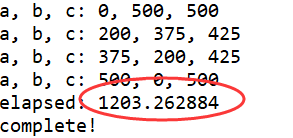
1 import time 2 start_time = time.time() 3 # 注意是两重循环 4 for a in range(0, 1001): 5 for b in range(0, 1001-a): 6 c = 1000 - a - b 7 if a**2 + b**2 == c**2: 8 print("a, b, c: %d, %d, %d" % (a, b, c)) 9 10 end_time = time.time() 11 print("elapsed: %f" % (end_time - start_time)) 12 print("complete!")
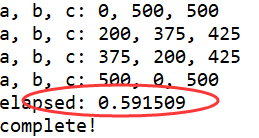
由上可知,明显第二个算法所花时间更少,更好。
由此得出结论:实现算法程序的执行时间可以反应出算法的效率,即算法的优劣。
但是,单纯依靠运行的时间来比较算法的优劣并不一定是客观准确的!
程序的运行离不开计算机环境(包括硬件和操作系统),这些客观原因会影响程序运行的速度并反应在程序的执行时间上。
如何客观评判一个算法的优劣呢?
时间复杂度与“大O记法”
假定计算机执行算法每一个基本操作的时间是固定的一个时间单位,那么有多少个基本操作就代表会花费多少时间单位。算法对于不同的机器环境而言,确切的单位时间是不同的,但是对于算法进行多少个基本操作(即花费多少时间单位)在规模数量级上却是相同的,由此可以忽略机器环境的影响而客观的反应算法的时间效率。
如何理解“大O记法”:
对于算法的时间性质和空间性质,最重要的是其数量级和趋势,这是计算算法效率的主要部分。而计算算法基本操作数量的规模函数中那些常量因子可以忽略不计。
最优时间复杂度/最坏时间复杂度/平均时间复杂度
我们主要关注算法的最坏情况,即最坏时间复杂度。
时间复杂度的几条基本计算规则
1、基本操作,即只有常数项,认为其时间复杂度O(1)
2、顺序结构,时间复杂度按加法进行计算
3、 循环结构,时间复杂度按乘法进行计算
4、分支结构,时间复杂度取最大值
5、判断一个算法的效率时,往往只需要关注操作数量的最高次项,其它次要项和常数项可以忽略
6、在没有特殊说明时,我们所分析的算法的时间复杂度都是指最坏时间复杂度。
第一个算法时间复杂度:T(n)=O(n*n*n)=O(n^3)
第二个算法时间复杂度:T(n)=O(n*n*(1+1))=O(n*n)=O(n^2)
由此可见,我们尝试的第二种算法要比第一种算法的时间复杂度好多了。
常见时间复杂度
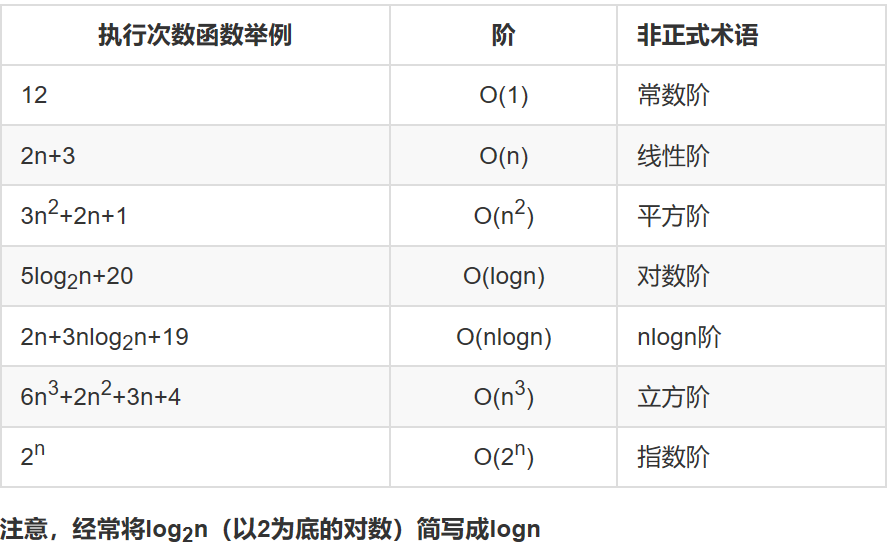
常见时间复杂度之间的关系
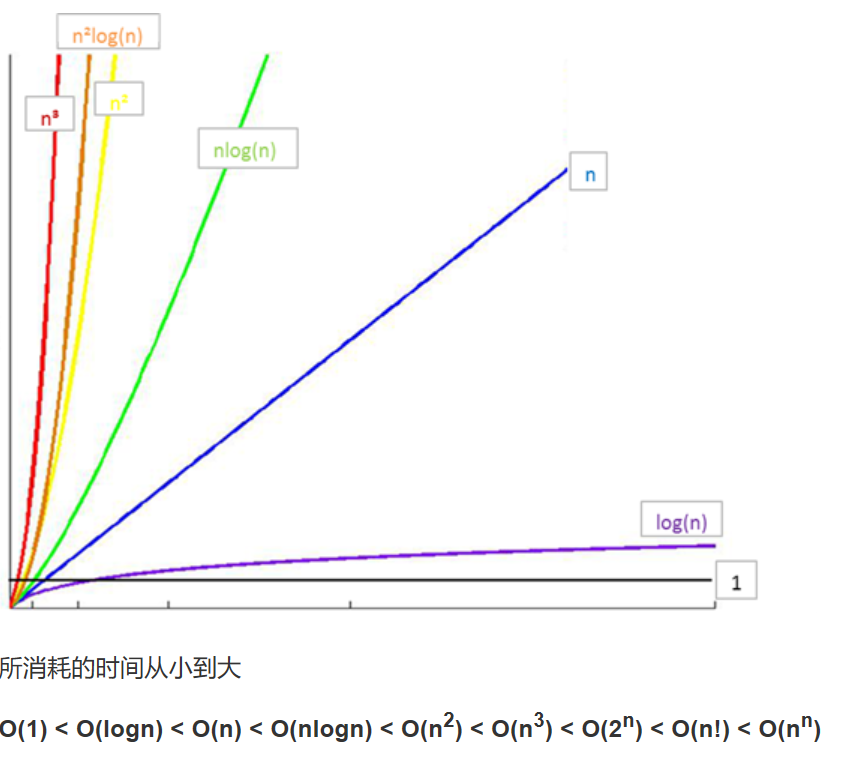
练习:时间复杂度练习(参考算法的效率规则判断)
O(5) ~~~O(1)
O(2n+1) ~~~O(n)
O(n^2+n+1) ~~~O(n^2)
O(3n^3+1) ~~~O(n^3)