字符串匹配(1)

我接触字符串匹配算法大概有一年半了（从八年级的四月份开始），但是目前为止，这些字符串匹配算法对我来说概念还是比较模糊，特此写一个专题，总结一下。

题目

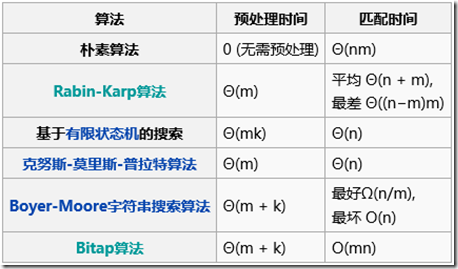
对于一个文本T，希望能找到与模式P相匹配的 T的子串T'的位置。其中，T的长度记为n，P的长度记为m，且总保证n>=m

朴素算法

其真正的时间复杂度应该为Θ((n-m+1)m)。

这种方法的好处在于易于理解，当m比较大时，此方法的优势非常大。

朴素算法的具体内容不做介绍。

Rabin-Karp算法

这种算法的时间复杂度不稳定。最差时和朴素算法一样O((n-m+1)m)。

对于长度为m的字符串s，可以建立一个映射hash(s)（hash表），得到一个值。此操作称为预处理。

比如：

// ASCII a = 97, b = 98, r = 114.

hash("abr") = (97 × 101²) + (98 × 101¹) + (114 × 101⁰) = 999,509

参见维基百科

这样，把每一个长度为m的T的子串都进行hash(T')运算，并与hash(P)比较，若hash(T')==hash(P)，则进一步比较T'与P即可。

利用有限自动机进行匹配

 

请参见算法导论583页，或维（伪）基（娘）百科

此算法的预处理时间为O(|∑|m)，匹配时间为Θ(n)。

有限自动机的概念：

1. 有限自动机，aka DFA，aka Deterministic Finite Automaton, aka 确定有限状态自动机，可以使用一个五元组表示

其中，Q为状态集，∑为字母表，δ是转移函数（），q0 是开始状态，F是终态集（接受状态集合）

2. ∑*（其中的*）被称作Kleensche Hülle，表示由∑所产生的所有可能的字符串的集合。比如{"ab", "c"}* = {ε, "ab", "c", "abab", "abc", "cab", "cc", "ababab", "ababc", "abcab", "abcc", "cabab", "cabc", "ccab", "ccc", ...}

3. 如果有限自动机在状态q时读入了字符a，则它从状态a变为状态δ(q,a)。每当当前状态q属于F，就说自动机M接受了迄今为止读入的字符串。

没有被接受的输入称为被拒绝的输入。

4. ϕ称为终态函数，它是从∑*到Q的函数，满足ϕ(w)是M在扫描字符串w后终止的状态。因此，当且仅当ϕ(w)属于F时，M接受字符串w。

ϕ的定义为：ϕ(ε)=q0, ϕ(wa)=δ(ϕ(w),a)

字符串匹配自动机的概念：

1. 定义一个辅助函数σ，表示一个从∑*到{0,1,2,…,m}的映射。

即：σ(x)=max{k: Pk后缀于k}

例如：对于P=ab，有σ(ε)=0, σ(ccaca)=1, σ(ccab)=2

2. 字符串匹配自动机的定义如下：

a) 状态集合Q={0,1,…,m}。

b) 开始状态q0是0状态，并且只有装填m是唯一被接受的状态。

c) 对于任意的状态q和字符a，状态转移函数定义为δ(q,a)=σ(P_qa)

3. 易证：ϕ(Ti)=σ(Ti)

ねね～上面这些学会了话，预处理就很容易写出来了。

#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
#include <algorithm>

using namespace std;
const int SigmaSize=3,MAXM=1000;
const string Sigma="abc";
string T,P;
int State[MAXM][SigmaSize+1]={0};
void init_delta(){
    for (int i=0;i<=P.size();i++){  /*注意此处要写<=*/ 
        for (int j=0;j<SigmaSize;j++){
            string patt,temp;
            temp=P.substr(0,i)+Sigma[j];
            int k=min(i+1,(int)P.size());      /*i+1的大小不能超过m*/ 
            patt=P.substr(0,i+1);
            if (temp.size()>patt.size()) temp=temp.substr(1,temp.size()-1);
            cout<<i<<":"<<endl<<temp<<endl<<patt<<endl;
            while (temp!=patt&&k!=0){
                k--;
                temp=temp.substr(1,temp.size()-1);
                patt=patt.substr(0,patt.size()-1);
            }
            State[i][j]=k;
        }
    }
}
            

int main(){
    freopen("String_DFA.in","r",stdin);
    cin>>T>>P;
    init_delta();
    return 0;
}

 然而，毕竟我技不如人，别人写的代码怎么看我都觉得惊叹不已。放上别人的代码对比一下吧。

bool cmp(char p[],char j,int k,int l)
{
     int ret = (p[k-1]==j);
     if( ret == 0 ) return true;
     for(int i = 0;i<k-1;++i)
        if(p[l-k+1+i] == p[i]) ++ret;
     return !(ret == k);
}
int transition(char p[])
{
    int m = strlen(p);
    for(int i=0;i<=m;++i)
    {
        for(int j=0;j<=255;++j)//这是精华所在啊！以为ascii中刚好256个字符所以这里代表了整个字符。
        //所以不管什么字符都不要处理。但是缺点是占用大量的空间。 
        {
            int k = ((m+1<i+2)?m+1:i+2);
            int l = i;
            do
            {
                k = k-1;
            }while(k>0&&cmp(p,j,k,l));
            t[i][j] = k;
        }
    }
    return m;
}

void fsm(char s[],char p[])
{  
    int n = strlen(s);
    int m = transition(p);
    int q = 0;
    for(int i = 0;i<n; ++i)
    {
        q = t[q][s[i]];
        if( q == m )
        {
            printf("Pattern occur with %d 
",i+1-m);
        }
    }
    putchar('
');
}

参考资料：

1. 刘汝佳. 算法竞赛入门经典（第二版）. 北京：清华大学出版社，2009

2. Thomas H. Cormen等. 算法导论（第三版）. 北京：机械工业出版社，2013