线段树初步

Segment Tree

线段树是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。

功能：单点、区间的修改、查询

建树

建树开N的4倍空间（注意，开2倍会访问无效内存）

为什么呢？我们看一看下面这张图：

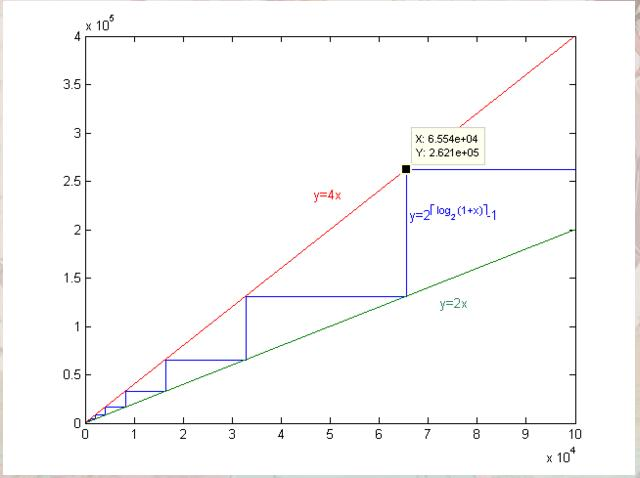
倍数= N(max)/No    -->No也相当于区间的长度。
N(max)可以看做是一个满二叉树（最好的情况）。N(min)可以看做最后一层只有两个子节点的树（最坏的情况）。

const int N = 100000;

struct node
{
    int l,r,v,f;
}tree[4 * N + 50];// 开4倍N的空间  

long long int sum = 0;

void build(int l,int r,int rt)
{
    // 初始化 l、r 
    tree[rt].l = l;
    tree[rt].r = r;
    if(l == r)
    {
        scanf("%d",&tree[rt].v);
        return;
    }
    
    int mid = l + r >> 1;
    build(l,mid,rt << 1);
    build(mid + 1,r,rt << 1 | 1);
    
    // 更新 v 
    tree[rt].v = tree[rt << 1].v + tree[rt << 1 | 1].v;
    return;
}

下传懒标记

void passdown(int k)
{
    // 下传懒标记 
    tree[k << 1].f += tree[k].f;
    tree[k << 1 | 1].f += tree[k].f;
    // 更新 v 
    tree[k << 1].v += tree[k].f * (tree[k << 1].r - tree[k << 1].l + 1);
    tree[k << 1 | 1].v += tree[k].f * (tree[k << 1 | 1].r - tree[k << 1 | 1].l + 1);
    // 还原根节点的懒标记 
    tree[k].f = 0;
}

查询

void query(int L,int R,int rt)
{
    int l = tree[rt].l,r = tree[rt].r;
    
    if(L <= l && R >= r)//如果当前区间为目标区间的子区间 
    {
        sum += tree[rt].v;
        return;
    }
    if(tree[rt].f)passdown(rt);//如果有懒标记要及时下传更新 
    int mid = l + r >> 1;
    // 二分寻找目标区间的子区间 
    if(L <= mid) query(L,R,rt << 1);
    if(R > mid) query(L,R,rt << 1 | 1);
}

区间更新

void update(int L,int R,int rt,int add)
{
    int l = tree[rt].l,r = tree[rt].r;
    
    if(L <= l && R >= r)
    {
        tree[rt].v += add * (r - l + 1);// v 加上该区间中所有元素要加上的总值 
        tree[rt].f += add;// 更新 懒标记 
        return;
    }
    
    if(tree[rt].f) passdown(rt)// 扫下一层之前必须下传懒标记                                                                                                                                                                                                            ;
    int mid = l + r >> 1;
    if(L <= mid) update(L,R,rt << 1,add);
    if(R > mid) update(L,R,rt << 1 | 1,add);
    
    tree[rt].v = tree[rt << 1].v + tree[rt << 1 | 1].v;    // 更新 v 
}

是 （R - L）不是（L - R）！就因为这个手残我卡了半个小时

模板题

POJ - 3468 

进阶题

（从求区间和变为求最大值）

P4513 HDU - 4630 HDU - 5726 HDU - 1166 HDU - 1754 

 

不用下传的版本：

void update(int L,int R,int val,int l,int r,int rt)
{
    tree[rt].v += (ll)(R-L+1) * val;
    if(L == l && R == r)
    {
        tree[rt].f += val;
        return;
    }
    int m = l + r >> 1;
    if(R <= m )
        update(L,R,val,l,m,rt << 1);
    else if(L > m)
        update(L,R,val,m+1,r,rt << 1 | 1);
    else update(L,m,val,l,m,rt << 1),update(m+1,R,val,m+1,r,rt << 1 | 1) 
} 

int query(int L,int R,int l,int r,int rt,int add)
{
    if(L == l && R == r)
        return tree[rt].v + add * (r-l + 1);
    int m = l + r >> 1;
    if(R <= m)
        return query(L,R,l,m,rt << 1,add + tree[rt].f);
    else if(L > m)
        return query(L,R,m + 1,r,rt << 1 | 1,add + tree[rt].f);
    else return query(L,m,l,m,rt << 1,add + tree[rt].f) + query(m + 1,R,m + 1,r,rt << 1 | 1,add + tree[rt].f);
}